Контрольная 3

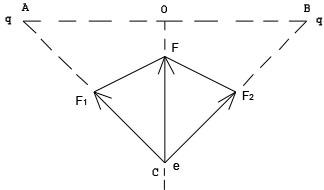
301. Два одинаковых неподвижных положительных заряда по q=1,6•10-19 Кл расположены на расстоянии см друг от друга. Вдоль перпендикуляра, проходящего через середину отрезка, соединяющего эти заряды, движется электрон. В какой точке этого перпендикуляра сила взаимодействия электрона и системы неподвижных зарядов максимальна?

F-сила взаимодействия электрона е и системы зарядов. Найдем ее выражение.

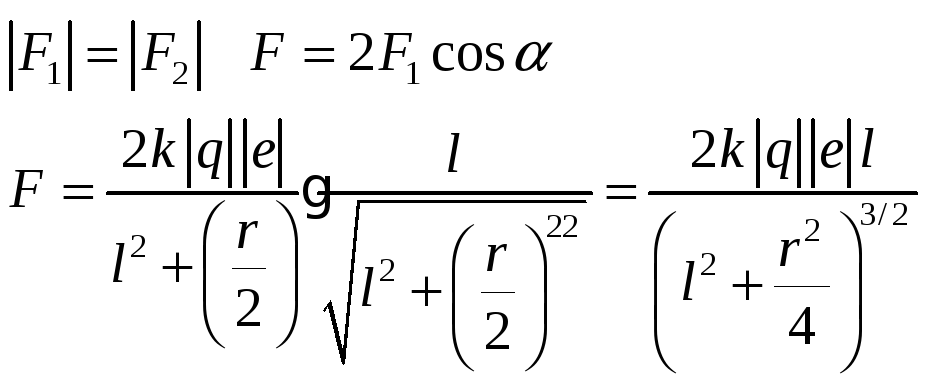
Найдем производную силы F по .

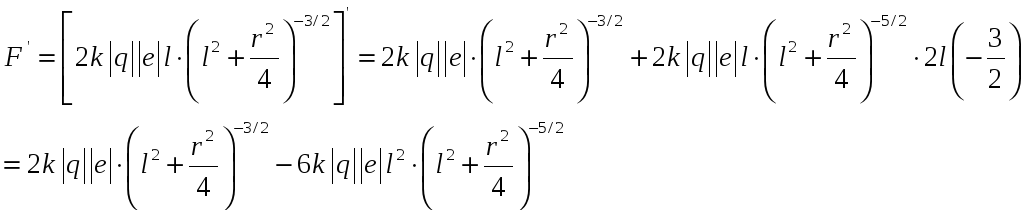
Прировняв производную к нулю, тогда:

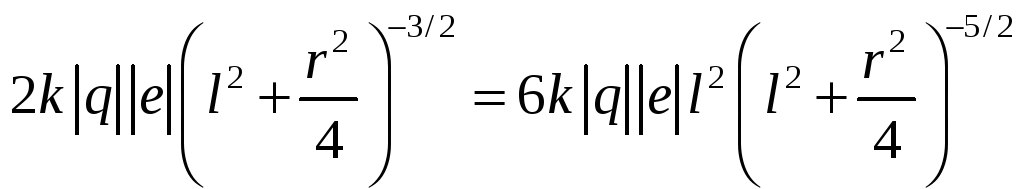
Сократив обе части на 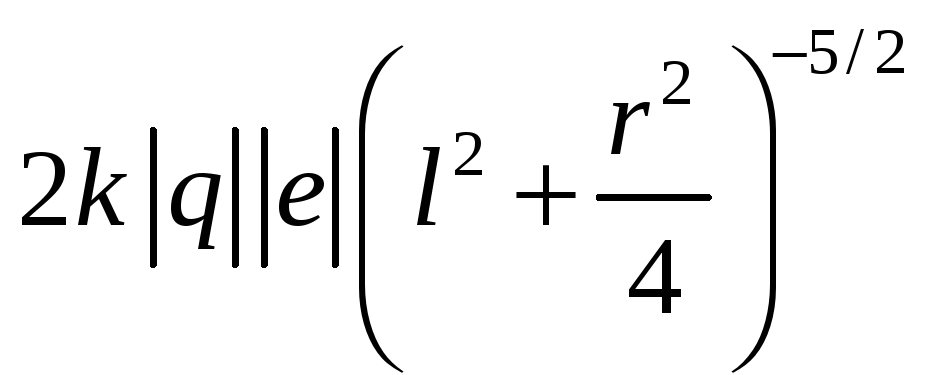получим:

Найдем , подставив численное значение r

Ответ м.

320. Тонкое кольцо равномерно заряжено с поверхностной плотностью заряда б. Найти потенциал и напряженность поля на оси кольца как функцию расстояния r от плоскости кольца, если внутренний радиус кольца a, внешний - b .

Решение.

Выделим в широком кольце очень узкое кольцо шириной . На этом кольце выделим заряд и будем считать его точечным зарядом. Такой заряд создается в точке М 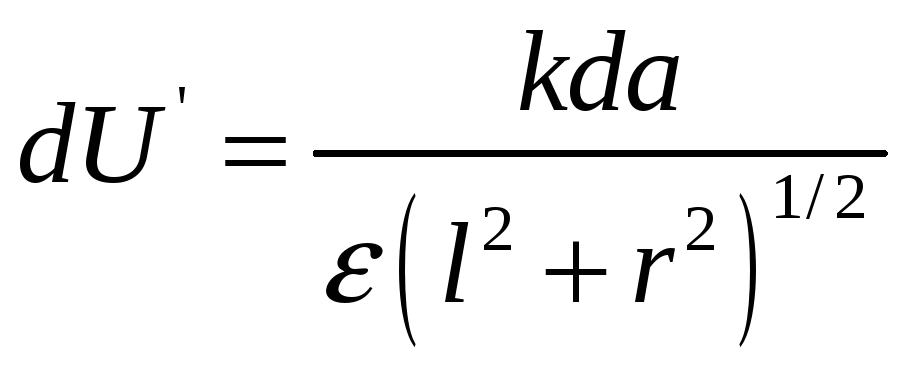, а так как заряд узкого кольца равен то потенциал создаваемый в точке М узким кольцом :

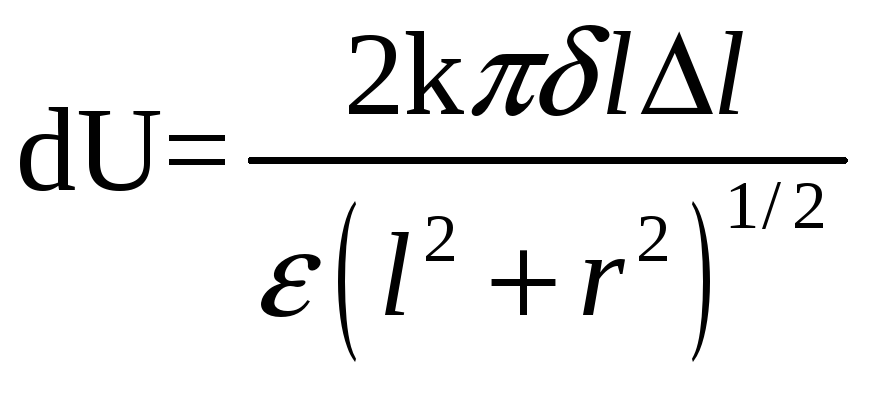
Чтобы найти потенциал создаваемый широким кольцом, надо суммировать потенциалы создаваемые всеми узкими кольцами от а до b:

Теперь найдем выражение для напряженности в точки М. Значение вектора ,создаваемого зарядом в точки М равно:

Напряженность создаваемое узким кольцом в точки М равно :

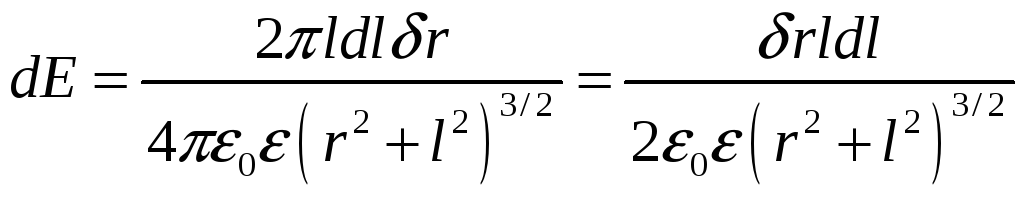
Величина результирующего напряжения электрического поля равна

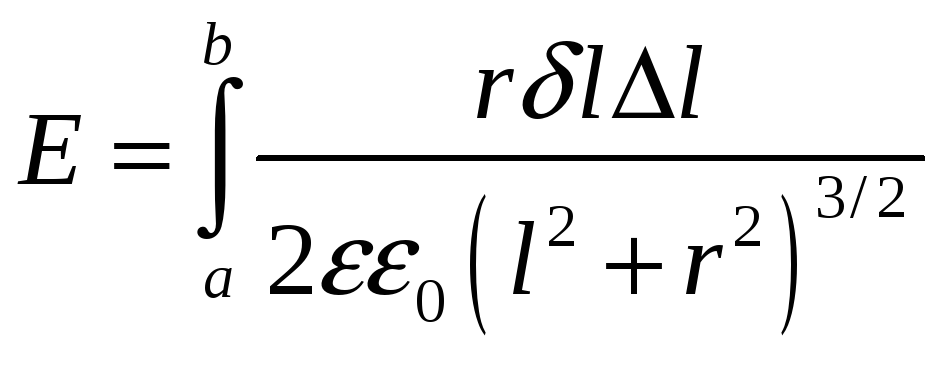
Ответ ,

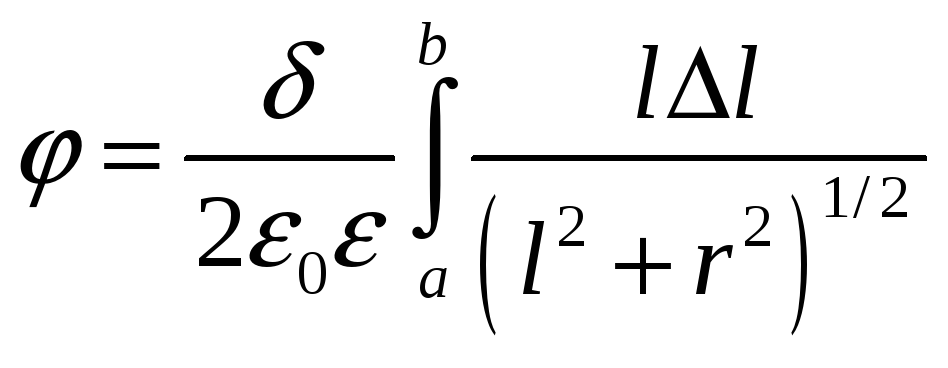
329. Потенциал поля внутри заряженного шара зависит только от расстояния r до его центра по закону гдз a и b - константы. Найти вектор напряженности поля , его модуль и распределение объемного заряда внутри шара.

338. Бесконечно длинный цилиндр радиусом R имеет положительный объемный заряд, объемная плотность которого зависит только от расстояния r от его оси по закону , где -константа. Полагая диэлектрическую проницаемость цилиндра и окружающего его пространства равной единице, найти напряженность электрического поля как функцию расстояния r: а) внутри цилиндра E1; б) вне цилиндра E2.

Решение

В качестве поверхности через которую будем определять поток вектора выберем цилиндр радиусом r и высотой h имеющий ту же ось симметрии что и заданный цилиндр. Поток вектора через боковую поверхность цилиндра

Из теоремы Гаусса следует, что

Приравниваем выражения и находим

Чтобы найти для окружим заданный цилиндр цилиндрической поверхности радиуса и высотой h ось симметрии по которой совпадает с осью цилиндра. По аналогии с первым случаем.

Поток вектора через боковую поверхность цилиндра

Из теоремы Гаусса следует, что

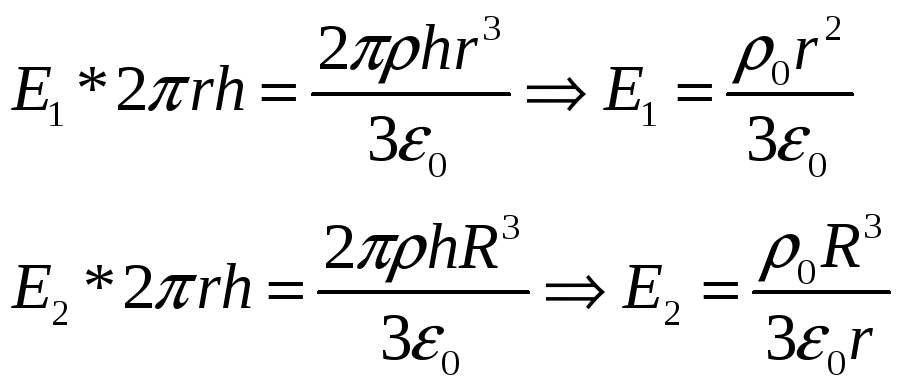
Приравниваем выражения и находим

Ответ,

347. Между пластинками плоского конденсатора находится диэлектрик (=6). Площадь пластин конденсатора S = 200 см2. Пластинки притягиваются друг к другу с силой F=2,5 мН. Найти поверхностную плотность связанных зарядов на поверхности диэлектрика.

Решение.

Чтобы определить поверхностную плотность связанных зарядов на поверхности диэлектрика воспользуемся формулой:

Сила взаимодействия пластин:

Так как :

Подставим и получим:

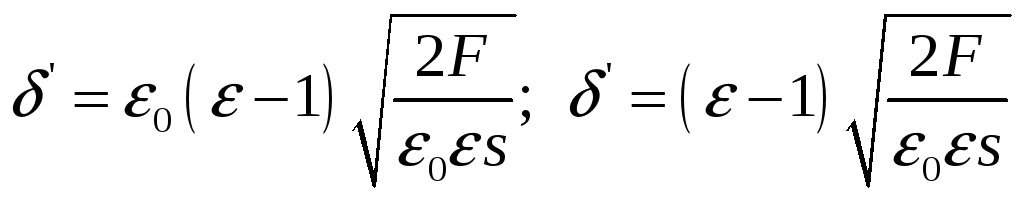
Ответ

356. По теории Бора электрон в атоме водорода вращается вокруг ядра по круговой орбите радиусом нм. Найти: а) скорость вращения электрона; б) кинетическую, потенциальную, и полную W энергию электрона.

Решение.

На электрон вращающийся по окружности во круг ядра действует со стороны ядра сила притяжения определяемая по закону Кулона.

Так как электрон вращается по окружности, то эта сила создается электрону центростремительное ускорение.

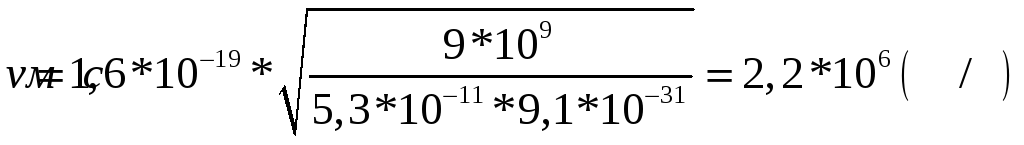
Найдем кинетическую энергию:

Найдем потенциальную энергию:

Ответ, , .

365. Каково будет отношение плеч l2/l1 при равновесии в мостике, изображенном на рис. 3.12, если в другие его плечи включены лампы? При каких условиях можно ответить на этот вопрос, имея в своем расположении' только данные, указанные на цоколях ламп?

374. Найти количество теплоты, выделяемой в единицу времени веществом с удельным сопротивлением = 109 Ом.м, которое заполняет все пространство между двумя сферическими оболочками. Радиусы оболочек а=I см и b =2 см, между ними поддерживается разность потенциалов U = 1000 В.

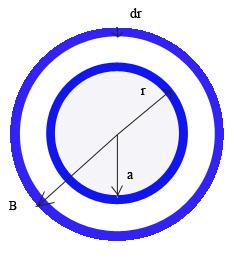
Решение

Количество теплоты выделяемой в еденицу времени вещества между сферическими оболочками найдем по формуле : 1111111

Найдем сопротевление 11. Для проводника длиной 11 и плошодью поперечного сечения 11111111