17.Уравнение плоской волны. Скорость распространения упругих волн. Волновое уравнение.

Рассм. некоторую точку среды В, находящуюся от источника на расстоянии х. Если колебания точек, лежащих в плоскости х=0 описываются выражением S(0,t)=A sin t, то колебание точки В будет совершаться по тому же закону, но колебания будут отставать по времени на  от колебаний источника: S(x,t)=A sin (t-), =x/v - время, за которое возмущение(волна) достигнет точки (частицы) В, где v – скорость распр. волны. Тогда колебание любой точки, вовлеченной в волновой процесс:S(x,t)=A sin (t -x/v)

S(x,t)=A sin (t -kx) (1)

k=x/v – волновое число, а (1) – ур-е плоской монохроматической волны. Более общее ур-ние (1) можно записать в виде S(x,t)=A sin (t –kx+), где А – ампл волны (t)= t –kx+ - фаза волны.

уравнение вида , где– функция координат и времени,иконстанты, называетсяволновым уравнением.

А теперь вернёмся к уравнениям Максвелла. Мы там получили, что . Для магнитного поля аналогично. Такая функцияудовлетворяет этому уравнению. При условии, что. Значит, должны быть электромагнитные волны, распространяющиеся с такой скоростью. И вот тут уже круг замкнулся. Максвелл получил волновое уравнение и определил скорость волны, а к тому времени было известно экспериментальное значение скорости света, и обнаружилось, что эти скорости равны.

18.Электромагнитные волны. Уравнение электромагнитной волны как решение уравнений Максвелла. Скорость распространения электромагнитных волн. Свойства электромагнитных волн.

Основные свойства электромагнитных волн.

1. Конечная скорость распространения электромагнитных возмущений. До возникновения теории Максвелла считалось, что все изменения эл или магнитного поля происходят мгновенно во всем пространстве, занимаемом этим полем.

2. Существование свободного электромагнитного поля. Если электрическое поле может существовать в отсутствие зарядов, при наличии изменяющегося магнитного поля, а магнитное поле – в отсутствие токов, при изменении электрического поля, то можно предположить, что в природе существует совокупность электрического и магнитного полей, органически связанных друг друга. Такое электромагнитное поле, не связанное с зарядами и токами, может существовать в отсутствие вещества и его называют свободным электромагнитным полем.

3. Электромагнитная теория света. Совпадение скорости распространения электромагнитных волн со скоростью света навело Максвелла на мысль о том, что свет представляет собой свободное электромагнитное поле. Эта гениальная догадка подтверждалась следующими фактами. Рассматривая распространение электромагнитных волн в среде с диэлектрической проницаемостью и магнитной проницаемостью, Максвелл показал, что их скорость в этом случае определяется формулой

Следовательно, на границе этой среды с вакуумом электромагнитные лучи должны преломляться и показатель преломления будет равен

Определив по этой формуле показатель преломления для ряда диэлектриков, Максвелл обнаружил совпадение с экспериментальными данными 1.

Из уравнений Максвелла можно вывести основные закономерности свойств световых волн и, в частности, потерю полуволны при отражении света от оптически более плотной среды.

4. Давление электромагнитных волн. Если электромагнитная волна встречает на своем пути проводящую поверхность (рис.206), то ее электрическое поле вызовет появление электрического тока, а магнитное поле действует на этот ток с силой, направление которой находится по правилу левой руки (рис.207). Эта сила направлена в сторону распространения электромагнитной волны: свободное электромагнитное поле производит давление на тела, в которые оно проникает 2. Т.k. свет представляет собой свободное электромаг поле, то из теории Максвелла вытекает существование светового давления.

5. Инертная масса свободного электромагнитного поля. Если свет давит на тела и может привести их в движение, т.е. сообщить некоторый импульс, то он сам обладает импульсом. Из теории Максвелла следует, что электромагн полю с энергией W соответствует импульс.

Выражая импульс как произведение массы на скорость:, откуда,

определяем инертную массу поля:.

Это соотношение между массой и энергией свободного электромагнитного поля является универсальным законом природы. Как показал Эйнштейн (1879-1955), оно справедливо для любого тела, если под энергией понимать его полную энергию, соответствующую всем видам движения, связанным с этим материальным объектом.

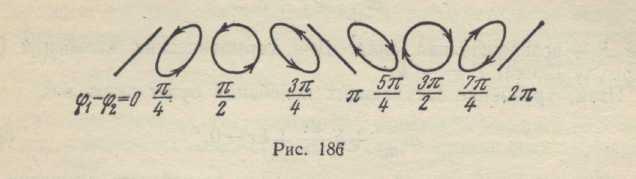
Траектория движения точки, получающиеся в результате сложения двух взаимно перпендикулярных колебаний одинакового периода и одинаковой амплитуды при различных разностях фаз, представлены на рис.186.

При сложении двух взаимно перпендикулярных колебаний с разными периодами получаются траектории более сложного вида, которые носят название фигур Лиссажу. На рис.187 показаны эти траектории для некоторых частных случаев.