15.Сложение взаимно перпендикулярных гармонических колебаний с равными частотами. Фигуры Лиссажу.

Пусть складываются два взаимно перпендикулярных колебания одинакового периода. Их уравнения будут иметь вид

Установим, какое движение возникает в результате сложения этих колебаний. Прежде всего, можно утверждать, что траектория результирующего движения будет расположена в прямоугольнике, стороны которого параллельны осям координат и равны соответственно 2A₁ и 2A₂. Для того чтобы получить уравнение траектории, надо из уравнений (218) исключить время. Рассмотрим несколько частных случаев.

1. Пусть . Тогда, поделив почленно уравнения (218):

Получаем Траектория представляет собой прямую, проходящую в I и III четвертях.

2. Пусть разность фаз колебаний равна , т.е., откуда. Тогда первое уравнение системы (218) можно переписать таким образом:

Поделив почленно уравнения (218), получаем .

Траекторией и в этом случае будет прямая, но проходит она во II и IV четвертях.

Найдем расстояние колеблющейся точки от начала координат как функцию времени для обоих случаев. Обозначим это расстояние через z. По теореме Пифагора,

,или ,

а это есть уравнение гармонического колебательного движения.

Таким образом, если разность фаз слагающихся колебаний равна 0 или , то результирующее колебание представляет собой гармоническое колебание, происходящее по прямой с тем же периодом и амплитудой, равной

.

2. Пусть . Тогдаи первое уравнение системы (218) можно представить следующим образом: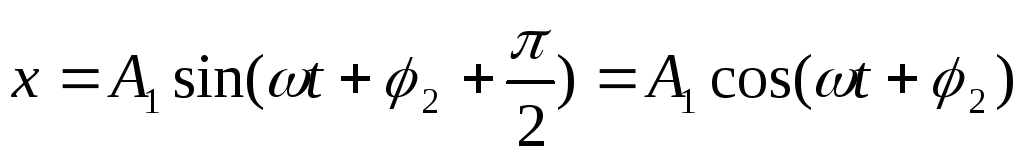.Система уравнений будет выглядеть так:

Отсюда получаем,

А это есть уравнение эллипса.

4. Совершенно аналогично можно получить такое же уравнение эллипса и для случая, когда , при этом точка движется по эллипсу против часовой стрелки, тогда как в предыдущем случае она движется по часовой стрелке.

При произвольной разности фаз траектория будет эллипсом, не приведенным к осям координат и вписанным в прямоугольник со сторонами . 2A₁ и 2A₂

25.Явление дифракции и ее объяснение на основе принципа Гюйгенса-Френеля.

Дифракция – совокупность явлений, наблюдаемых при распространения света в среде с резкими неоднородностями и связанных с отклонениями от законов геометрической оптики.

Пусть S на рис представляет одну из волновых поверхностей света, распространяющегося от некоторого источника. Амплитула светого колебания в точке Р, лежащей перед этой поверхностью, м б согласно Френелю найдена из следующих соображений. Каждый элемент поверхности служит источником вторичной сферической волны, амплитуда кот пропоциональна величине элемента dS. Амплитуда сферической волны убывает с расстоянием r от источника по з-ну 1/r . сл-но от каждого участка dS волновой поверхности в точку Р приходит колебание:

В этом выражении - фаза колебания в месте расположения волновой поверхностиS, k – волновое число, r – раст-ине от элемента поверхности dS до точки Р.величиеа а0 опр-ся амплитудой светого колебания в том месте, где находится dS. Коэффициент пропорциональности К Френель считал убывающим при увеличении угла φ между нормалью n к dS и направлением от dS и направлением от dS к точке Р и обращающимся в 0 при

Результирующее колебание в точке Р представляет собой суперпозицию колебаний, взятых для всей волновой поверхности S:

- аналитическое выражение принципа Гюйгенса-Френеля.