физика, кр1, вар1

КОНТРОЛЬНАЯ РАБОТА N1

Вариант №1

101.Уравнение движения частицы x=4+2t-0,5t³м. Найти координату, скорость и ускорение при t = 4 с.

Решение:

При t=4 c Модуль мгновенной скорости равен первой производной пути по времени, т.е. v=x`(t)=2-1.5t<sup>2</sup>=|2-1.5*16|=22 (м/с). Ускорение равно первой производной скорости по времени, т.е. a=v`(t)=-3t=|-3*4|=12 (м/с²).

Ответ: x=-20 м; v=22 м/с; a=12 м/с².

111. На частицу массой 100 г действует сила, зависящая от времени по закону F = 0,2t. Найти уравнение движения и путь за первые 2 с.

Решение:

Воспользуемся уравнением движения с постоянным ускорением . Среднее ускорение частицы , а, поскольку при t=0 F=0, то формула примет вид . Так как x₀=0, v₀=0, то уравнение движения — . Отсюда путь за первые 2 с s=x=2³/2=4 (м).

Ответ: ; s=4 м.

121. Найти момент инерции обруча массой m и радиусом R относительно оси, проходящей через диаметр обруча.

Решение:

Сделаем схематический рисунок. С учетом аддитивности момента инерции представим момент инерции обруча I как сумму моментов инерции двух половин обруча, т.е. I=2I₁.

Воспользуемся формулой для непрерывного распределения масс , где — масса элементарного участка(dr- длина такого участка), на которые мы разобьем обруч. Получаем .

. Момент инерции обруча найдем интегрированием: .

Ответ: .

131. На вращающейся скамье Жуковского  = 8 рад/с стоит человек со стержнем длиной 2 м, массой 10 кг. Найти угловую скорость и произведенную работу, если стержень, стоящий вертикально по оси скамьи, повернуть горизонтально, симметрично оси. Суммарный момент инерции скамьи и человека равен 4 кг м².

Решение:

Поскольку система замкнута, т.е. L=const, то Iω=I­­­­₁ω₁, где I₁=I+I_ст, а момент инерции стержня I_ст=ml²/12=3.33 (кг·м²). Отсюда (рад/с). Произведенную работу найдем из разности кинетической энергии: (Дж).

Ответ: 4,37 рад/с; 58 Дж.

141.Определить период колебаний стержня длиной 20 см около горизонтальной оси, перпендикулярной стержню и проходящей через его конец.

Решение:

Период колебаний физического маятника определяется выражением , где I - момент инерции стержня относительно оси вращения. По теореме Штейнера I=I₀+mx², где I₀ - момент инерции маятника относительно оси, проходящей через центр тяжести стержня O.

. Таким образом, при x=l/2=10 см с.

Ответ: 0,716 с.

151. Определить внутреннюю энергию U водорода, а также среднюю кинетическую молекулы этого газа при температуре Т = 300 К, если количество вещества  этого газа равно 0,5 моль.

Решение:

Внутренняя энергия газа определяется по формуле , i=5, т.к. водород- двухатомный газ. Отсюда (Дж). Средняя кинетическая энергия молекулы водорода

Ответ: U=3116.25 Дж; E=1.035*10^-20.

161.Определить количество теплоты Q, которое надо сообщить кислороду объемом V = 50 л при его изохорном нагревании, чтобы давление газа повысилось на  p = 0,5 МПа.

Решение:

Количество теплоты равно разности внутренних энергий газа после и до нагревания (0), i=5, т.к. кислород - двухатомный газ. Поскольку V=const, то . Отсюда (1). Из уравнения Менделеева-Клапейрона pV=vRT получим (2). Подставляя (1) и (2) в (0), найдем

(Дж)

Ответ: 62500 Дж.

171.Идеальный газ совершает цикл Карно при температурах теплоприемника Т₂ = 290 К и теплоотдатчика Т₁ = 400 К. Во сколько раз увеличится коэффициент полезного действия  цикла, если температура теплоотдатчика возрастет до Т ₁ = 600 К?

Решение:

КПД работы, совершаемой по циклу Карно, определяется формулой . Отсюда . Если температура теплоотдатчика возрастет до Т ₁ = 600 К, то коэффициент полезного действия увеличится в раз.

Ответ: 1,88 раз.

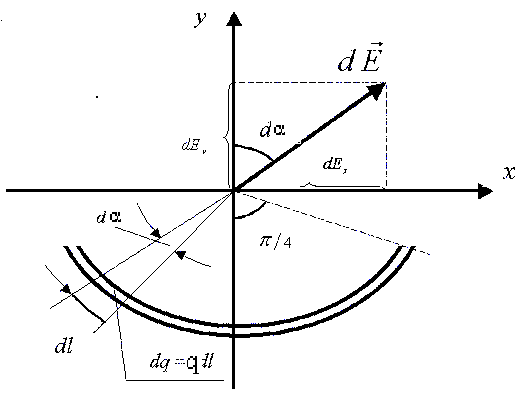
181. На тонкой нити, изогнутой по дуге окружности радиусом R=10см, равномерно распределен заряд q=20нКл. Определить напряженность поля E, создаваемого этим зарядом в точке, совпадающей с центром кривизны дуги, если длина нити равна четверти длины окружности.

Решение: Выберем оси координат так, чтобы начало координат совпадало с центром кривизны дуги, а ось Y была бы симметрично расположена относительно концов дуги. На нити выделим элемент длины dl. Заряд dq=qdl/l, находящийся на выделенном участке, можно считать точечным. Определим напряженность электрического поля в точке O: , где - радиус-вектор, направленный от элемента к точке, напряженность которой вычисляется.

Выразим вектор через проекции и на оси координат, где и - единичные векторы направлений (орты).

Напряженность найдем интегрированием:

.

Интегрирование ведется вдоль дуги длиной l. В силу симметрии этого найдем сначала напряженность dl поля, создаваемого зарядом dq тогда , где

Так как . Подставим выражение и приняв во внимание симметричное расположение дуги относительно оси Y, пределы интегрирования возьмем от 0 до π/4, а результат удвоим:

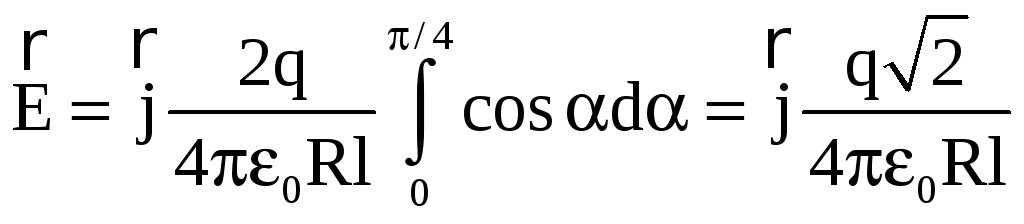. Выразим длину нити l через R: 4l=2πR, l= πR/2. Подставив, получим:

Ответ:

191. На пластины плоского конденсатора, расстояние между которыми d=3см, подана разность потенциалов U=1кВ. Пространство между пластинами заполняется диэлектриком (ε=7). Найти поверхностную плотность связанных зарядов. Задачу решить, если заполнение конденсатора диэлектриком производится: а) до отключения конденсатора от источника напряжения; б) после отключения конденсатора от источника напряжения.

Решение:

а) Если конденсатор подключен к источнику тока, то напряжение на нем остается постоянным. При наличии диэлектрика напряженность электрического поля между обкладками конденсатора E₁=U/d. Плотность связанных зарядов σ`₁=p_n, следовательно, поверхностная плотность связанных зарядов: æ. Откуда .

б) Если конденсатор отключен от источника тока, заряд на его обкладках остается неизменным. Тогда напряженность электрического поля между обкладками в отсутствие диэлектрика ; поверхностная плотность зарядов на положительно заряженной пластине . Так как σ₂=const, то после введения диэлектрика . Плотность связанных зарядов σ`₂=p_n, следовательно, поверхностная плотность связанных зарядов: æ.

Ответ: а) , б) .