Физика часть 1. Контрольная работа №1. Вариант №8

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Факультет НиДО

Специальность ПОИТ

Контрольная работа № 1

по дисциплине «Физика»

Вариант № 8

Выполнил студент: ********

группа ******

Зачетная книжка № ******-**

Электронный адрес ******@****.***

Минск 2011

Задача 108

Частица движется так, что ее скорость изменяется со временем по закону , где – время в секундах. В начальный момент времени частица находилась в точке с координатами . Найти: 1) зависимость от времени модуля скорости частицы; 2) зависимости от времени вектора ускорения и модуля ускорения; 3) кинематический закон движения частицы; 4) радиус-вектор в момент времени ; 5) модуль перемещения частицы за время .

Дано:

Найти:

Решение:

Найдем модуль вектора скорости, используя теорему Пифагора:

Из условия задачи:

; ;

Ускорение частицы найдем из определения ускорения:

Модуль ускорения также найдем из теоремы Пифагора:

Кинематический закон движения найдем, используя определение скорости:

; ;

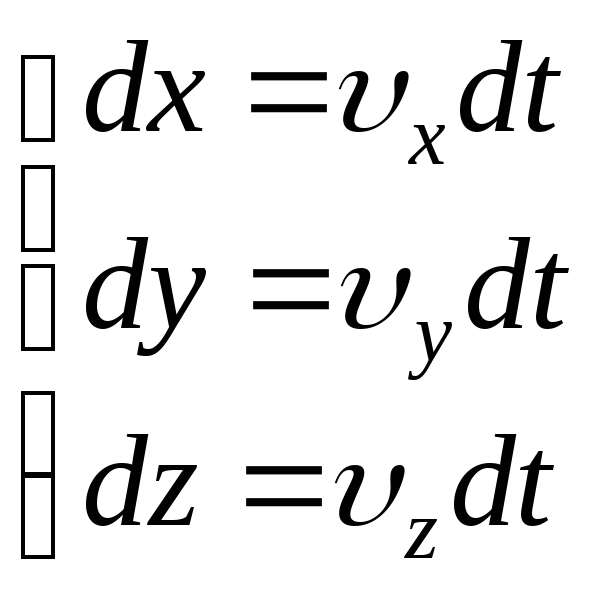
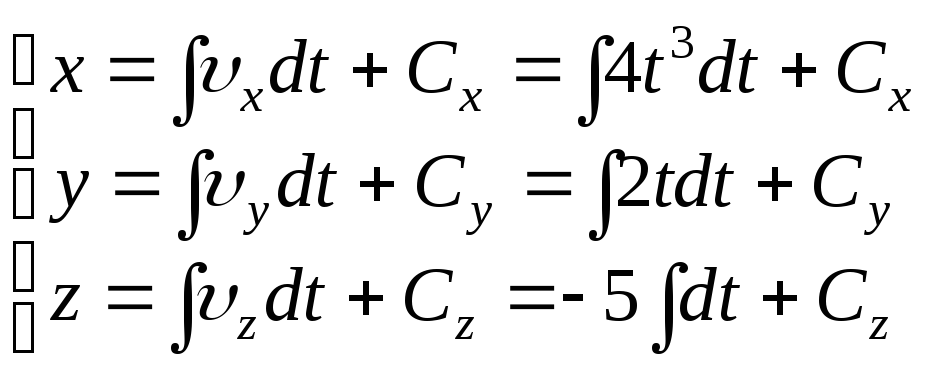
Константы , и найдем, используя начальные условия:

; ; ; ;

найдем, подставив в кинематический закон движения :

Вектор перемещения частицы:

Модуль вектора перемещения также находим используя теорему Пифагора

Ответ:

Задача 118

Сплошной однородный вертикальный цилиндр массой и радиусом начинает вращаться вокруг своей неподвижной оси под действием горизонтальной касательной силы, приложенной к боковой поверхности цилиндра. Модуль силы зависит от времени как , где – некоторая положительная постоянная. Найти угловую скорость цилиндра в момент времени после начала действия силы.

Дано:

Найти:

Решение:

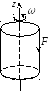Цилиндр начинает вращаться под

действием приложенной силы,

для описания его движения используем

основное уравнение динамики

вращательного движения: , в

проекции на ось вращения :

Момент инерции цилиндра

Момент внешней силы

Угловое ускорение по определению

Подставляем:

Сокращаем : Переносим переменные:

Интегрируем:

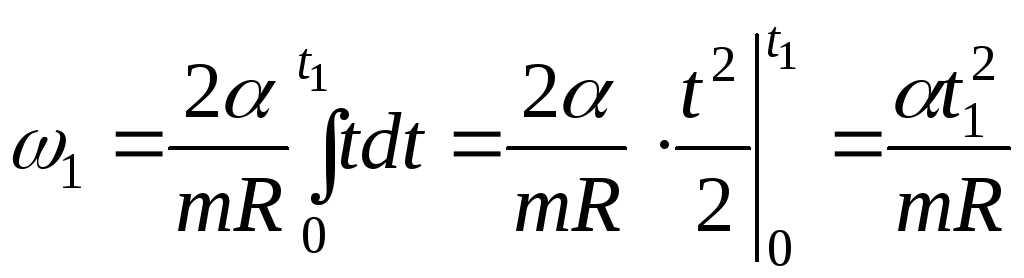
Ответ:

Задача 128

На железнодорожной платформе, равномерно движущейся со скоростью , жестко закреплено орудие, из которого произведен выстрел в сторону, противоположную ее движению, после чего скорость платформы стала равной . Определить модуль скорости снаряда относительно платформы, если вектор этой скорости составляет с горизонтом угол . Масса снаряда , масса платформы с орудием .

Дано:

Найти:

Решение:

Будем считать систему "платформа-орудие-снаряд" замкнутой.

В таком случае импульс этой системы будет сохраняться:

Запишем импульсы системы для начального и конечного состояний:

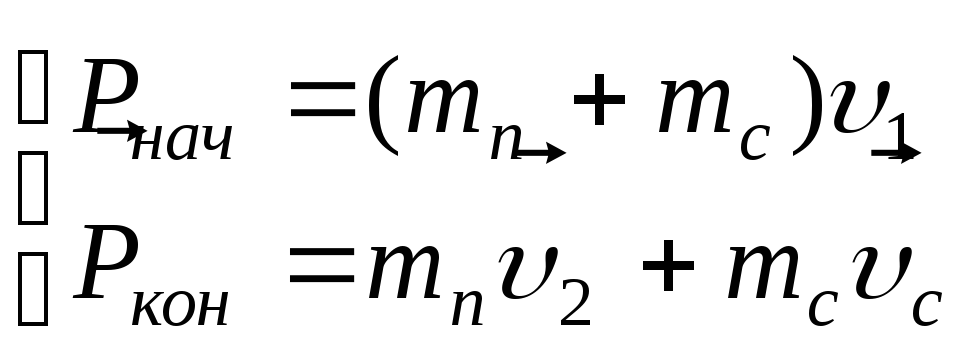
В данном случае рассматривается скорость снаряда относительно земли. Чтобы выразить скорость снаряда относительно платформы воспользуемся законом сложения скоростей:

и подставим:

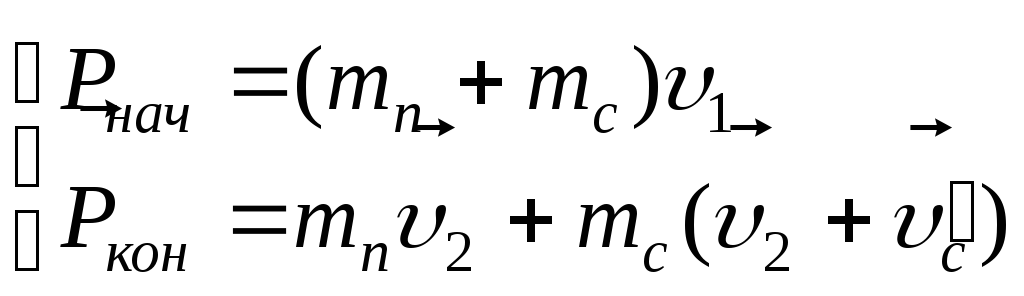
Приравниваем импульсы:

Спроецируем это уравнение на ось :

Преобразуем и выразим

Подставляем численные значения:

Ответ:

Задача 138

На краю скамьи Жуковского, вращающейся с угловой скоростью , стоит человек массой . Определить массу скамьи, если при переходе человека в ее центр угловая скорость вращения увеличилась до . Момент инерции человека рассчитывать как для материальной точки.

Дано:

Найти:

Решение:

Вращающаяся система "человек-скамья" является замкнутой момент импульса этой системы является постоянной величиной:

В этой системе происходит изменение момента инерции будет меняться и угловая скорость.

Подставляем:

Преобразуем и выразим :

Подставим численные значения:

Ответ:

Задача 148

При вертикальном запуске с поверхности Земли и выключении двигателя максимальная высота подъема ракеты над поверхностью Земли составила . На какой высоте над поверхностью Земли скорость ракеты была равна ? Принять, что на ракету действует только сила тяготения со стороны Земли, а масса ракеты остается постоянной. Масса Земли и ее радиус известны.

Дано:

Найти:

Решение:

По условию задачи на ракету не действует сила сопротивления воздуха полная механическая энергия ракеты остается постоянной на высоте и она одинакова.

Используем это выражение для высот и . Учтем, что на высоте скорость была , а на высоте скорость равна нулю:

Преобразуем и выразим :

,

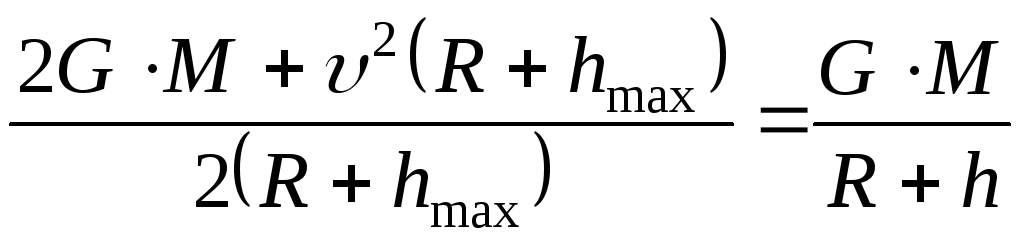
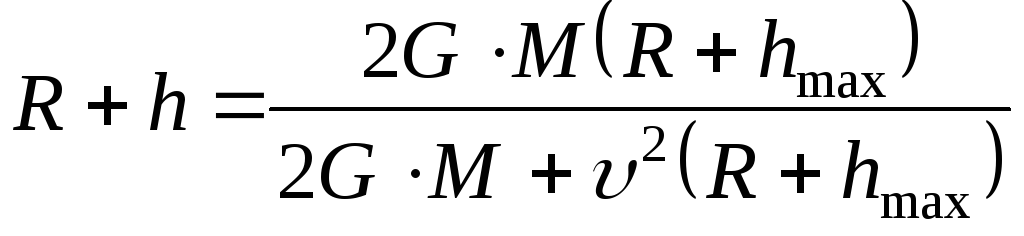
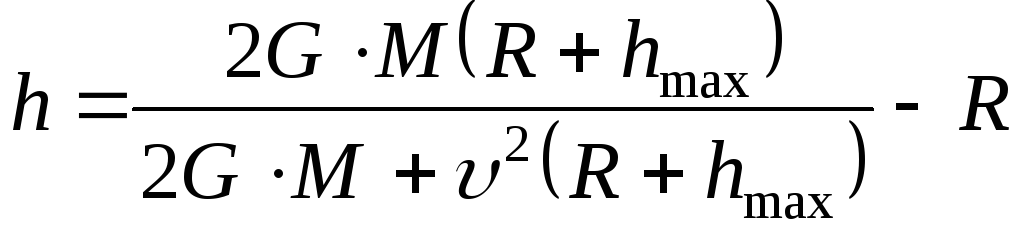где – масса Земли,

а – гравитационная постоянная

Ответ:

Задача 158

На конце тонкого однородного стержня массой укреплен грузик массой . Определить длину стержня, если период малых колебаний этой системы относительно горизонтальной оси, проходящей перпендикулярно стержню через его свободный конец, равен .

Дано:

Найти:

Решение:

П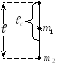ериод малых колебаний системы тел:

,

где – момент инерции системы тел относительно точки подвеса:

,

– масса системы тел: ,

– расстояние от центра тяжести системы до оси подвеса:

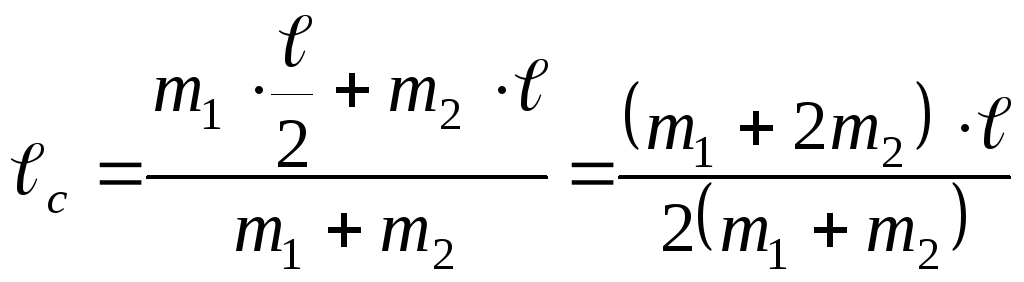
Возведем выражение для периода в квадрат и подставим выражения для , и :

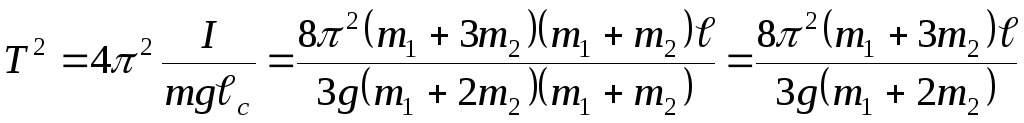
Выразим длину стержня:

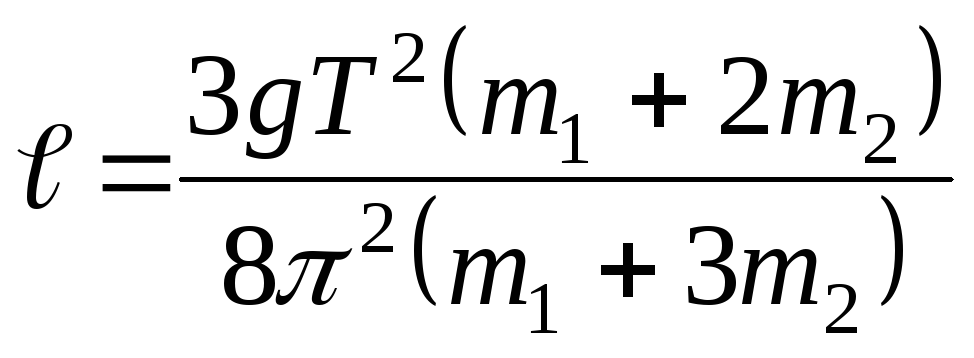
Ответ:

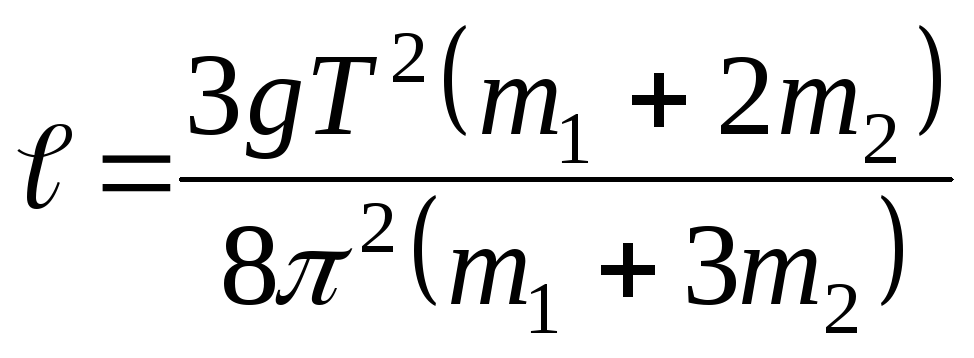
Задача 168

Частица массой совершает колебания вдоль оси по закону . Определить период колебаний частицы и энергию ее колебаний. Найти в момент времени проекцию вектора скорости и проекцию упругой силы.

Дано:

Найти:

Решение:

Частица совершает колебания по закону:

В данной задаче

;

Период связан с частотой:

Энергия колебаний:

, где – коэффициент упругости, который связан с частотой:

Подставим и найдем энергию:

Скорость частицы можно найти используя определение скорости:

Подставим заданное значение времени:

Сила упругости по закону Гука равна:

Подставим заданное значение времени:

Ответ:

Задача 178

Водород находится в равновесном состоянии, при котором средняя энергия теплового движения одной его молекулы составляет . Определить: 1) среднюю кинетическую энергию поступательного движения молекулы; 2) среднюю кинетическую энергию вращательного движения молекулы; 3) среднюю квадратичную скорость молекулы. Молекулу считать жесткой.

Дано:

Найти:

Решение:

Средняя энергия молекул: ,

где – число степеней свободы

Для жесткой двухатомной молекулы водорода

,

Средняя энергия теплового движения молекулы:

Средняя энергия поступательного движения молекулы:

Средняя энергия вращательного движения молекулы:

Из этих соотношений можно выразить и

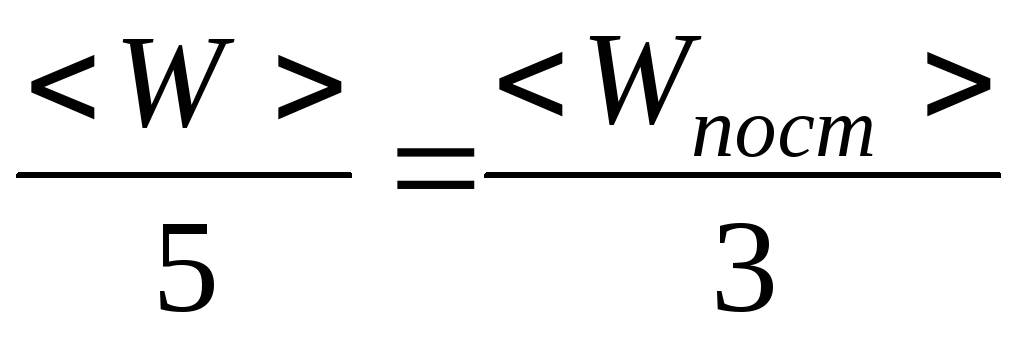
Средняя квадратичная скорость молекулы:

, где – масса одной молекулы.

,

где – молярная масса водорода,

– число Авогадро

Как было ранее рассчитано

Подставим численные значения:

Ответ:

Задача 188

Идеальный двухатомный (с жесткой связью) газ находится под давлением , занимая при этом объем V1 = 50 л. Над газом последовательно проводят следующие процессы: – изотермическое сжатие до объема ; – изобарное увеличение объема до ; – изохорное увеличение давления до . На Vp-диаграмме изобразить график процесса . Определить в ходе всего процесса: 1) изменение внутренней энергии газа; 2) работу сил давления газа; 3) количество теплоты, переданное при этом газу.