ЛЕКЦИИ
по
Теории Функций Комплексного Переменного
Автор: Каменский А.Г.
Набор: Шатов А.Н.
e-mail: nclog@bk.ru
2003г.
Лекция №1
Комплексные числа
Опр. x+iy – комплексное число, где x,y – действительные числа, i – мнимая единица.
;
Опр. Комплексное число – упорядоченная пара действительных чисел: z=(a,b).
Пусть
=(a,b);
=(c,
d);
+ =(a+c, b+d);
g = (ga, gb), где g – действительное число;
=(ac-bd, ad+bc);
(0,1)=i;
(0,1)(0,1)=(-1,0);
z=(x,y)=x(1,0)+y(0,1)=x+iy;
;
y
(x,y)
x
|z|
=
=
r;
arg
z=
= arctg
- аргумент комплексного числа;
Arg
z
=
+ 2
- главный аргумент;
z = r(cos
+ i*sin
)=
r
;
= cos + i*sin - формула Эллера.
=
+i
=
(cos
+i*sin
);
=
+i
=
(cos
+i*sin
);
= (cos( + )+i*sin( + ));
=
(cos
n
+sin
n
);
(cos
+
i*sin
),
k=0,1,…,n-1;
=
x-iy
z
=|z
=
;
Топология комплексной плоскости
Опр.
- расстояние между числами
.
Опр.
-окрестностью
z
называется множество всех таких точек
:
Опр.
=
w
Опр. Множество М называется замкнутым, если оно содержит все свои предельные точки.
Опр. Множество называется открытым, если каждая его точка принадлежит ему с некоторой ее окрестностью.
Опр. Множество называется связанным, если всякие его две точки можно соединить ломанной с конечным числом звеньев, целиком принадлежащих этому множеству.
Опр. Открытое связанное множество называется областью.
Опр. Множество называется односвязанным, если оно ограничено одной несамопересекающейся замкнутой кривой и оно связанное.
Опр. Множество называется двусвязанным, если оно ограничено двумя несамопересекающейся замкнутыми кривыми и оно связанное.
Функции комплексного переменного
Опр.
Если даны множества М и G
на комплексной плоскости и каждому z
из M
соответствует w
из G,
то говорят, что
функция
.
Опр. 
;
Опр.
(1)
-
степенной ряд.
Утв. Ряд (1) сходится
внутри круга
и расходится вне его. При
он
сходится равномерно.
Некоторые разложения:
;
;
;
Докажем формулу Эллера:
= cos + i*sin
;
;
-доказывается
умножением рядов.
;
;
Периодичность
функции
:
;
Опр.
=
,
если
Опр. Множество точек z: называется окрестностью бесконечно удаленной точки.
Лекция 2
Дифференцируемость функций комплексного переменного
Опр.
,
если этот lim
и не зависит от того, как
стремится к нулю.
Если z=z+iz,
то
Теорема.
Если
дифференцируема
в точке z
и
,то
в точке z
выполняются условия Коши-Римана:
Док-во:
Y
z+
z
z+
X
;
;
.
Теорема. Если u и v дифференцируемые функции в точке z и для них выполнены условия Коши-Римана, то w=u+iv будет дифференцируемой в точке z.
;
;
;
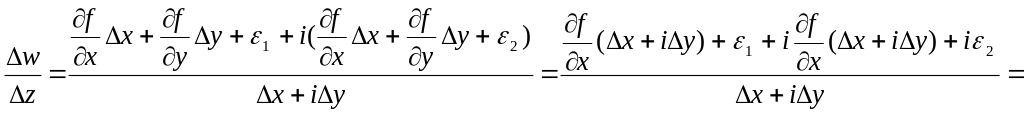
Опр. Функция f(z) наз. Аналитической в точке z, если она дифференцируема в точке z и в некоторой ее окрестности.
Пример.
условия Коши-Римана выполняются
Восстановление аналитической функции по ее действительной (мнимой) части.
Опр.
Функция
называется гармонической в области G,
если в этой области выполняются условие:
Утв. Если функция аналитическая, то ее действительная и мнимая части – гармонические функции.
Док-во:
;
;
т.к.
,
складывая эти равенства, получаем
,
т.е.
u – гармоническая функция. Аналогично v - гармоническая функция.
Доказано.
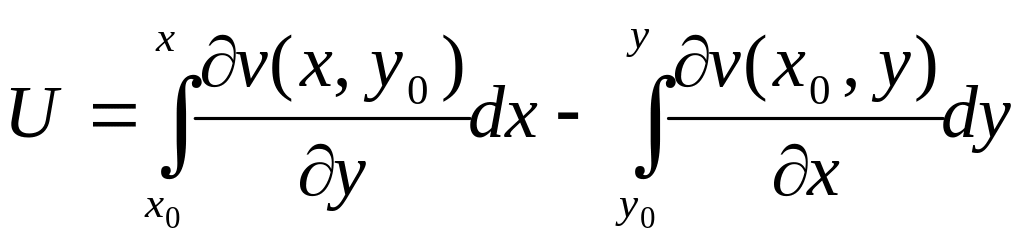
Пример.
Опр. Функция f(z) называется однолистной в области G, если:
Пример.
- не однолистная на всей плоскости
- однолистная в
области
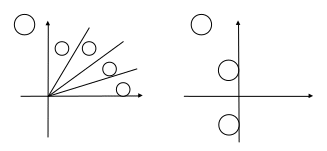
Поверхности Римана
1.
z
х
W v
-
+
-
-
+
y u
+
Разрежем плоскость W по лучу Ох. Верхний край первой плоскости соединим с нижним краем второй, верхний край второй соединим с нижним краем третей и т.д. до n. Верхний край n-ой плоскости склеим с нижним краем первой. Получим поверхность Римана для функции .
2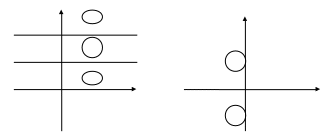
.
y + v
-
+
+
x u -
Лекция 3
Конформные отображения
Опр. Отображение обладающие свойствами консерватизма углов и постоянства растяжений называется конформным.
Теорема. Если
аналитическая функция в области G
в G,
то
задает конформное отображение области
G.
Док-во:
y
v
w
z
x
u
;
;
;
;
- постоянство
растяжений.
- консерватизм
углов.
Доказано.
1. Линейная функция.
1)
-
параллельный перенос.
2)
При линейном преобразовании прямые переходят в прямые, окружность переходит в окружность.
2. Дробно-линейная функция.
,
т.е. дробно-линейное преобразование
сводится к линейному и функции
.
Опр. Обобщенная окружность:
,
т.е. это окружность или прямая.
Теорема. Дробно-линейная функция отображает обобщенную окружность в обобщенную окружность.
Док-во:
- обобщенная окружность.
Опр.
Точки B
и С - сопряженные относительно окружности
Г, если любая окружность
,
проходящая через эти точки, ортогональна
Г.
Лемма. Если точки
В и С явл. Сопряженными относительно
окр-ти с центром О, А-точка пересечения
Г и
.,
то
.
Утв.
Если
дробно – линейное отображение, то
переводит точки, сопряженные относительно
окружности, в точки, сопряженные
относительно ее образа.
Z W
А С
В
O
;
,
т.е. сопряженными являются точки 0 и
.
Примеры решения задач:
Задача 1.
Отобразить полуокружность в единичный круг.
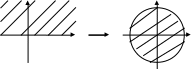Z
W
-1 1
Решение:
и
сопряженные относительно Ох, т.е.
действительная ось отображается в
окружность.
; 
-
искомое отображение.
Задача 2.
Отобразить отрезок в единичный круг.
Z
3i
i
Решение:
- отобразить отрезок в
;
;
;
;
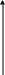
Задача 3.
Отобразить полосу в единичный круг.
2
Решение:
;
;
;
;
;
;
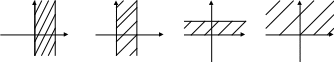
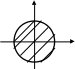
Функция Жуковского
; 
;
;
,
1)
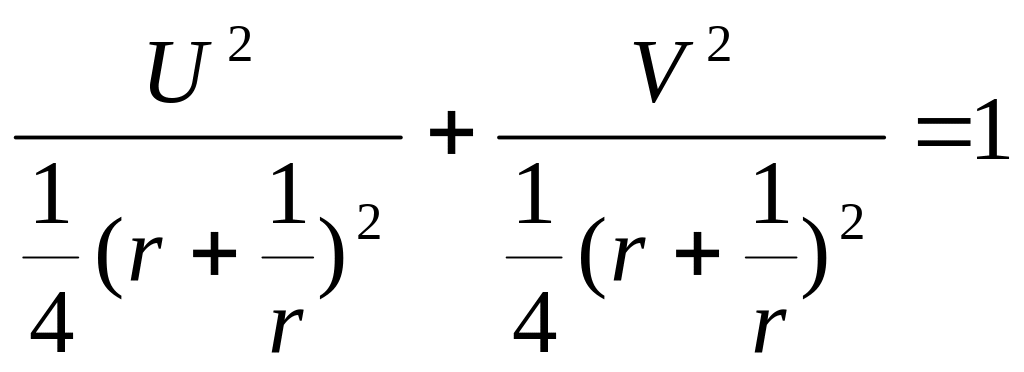- эллипс
2)
- функция, обратная
функции Жуковского.
Теорема Римана
Если G – односвязная область, граница которой состоит более чем из одной точки, то существует аналитическая функция, задающая конформное отображение G на единичный круг.
Лекция 4
Интеграл функции комплексного переменного
Пусть на комплексной плоскости задана кривая L - кусочногладкая, конечная, ориентированная.
;
Опр. - некоторая функция
,
где
.
Существование интеграла и методы его вычисления.
Утв1.
Если
;
u
и v
– непрерывные функции; дуга L
– кусочно гладкая, то
соответствующие криволинейные интегралы
и
.
Док-во:
Утв2.
Если
,
u
и v
– непрерывные, дуга L
– кусочно гладкая, то
.
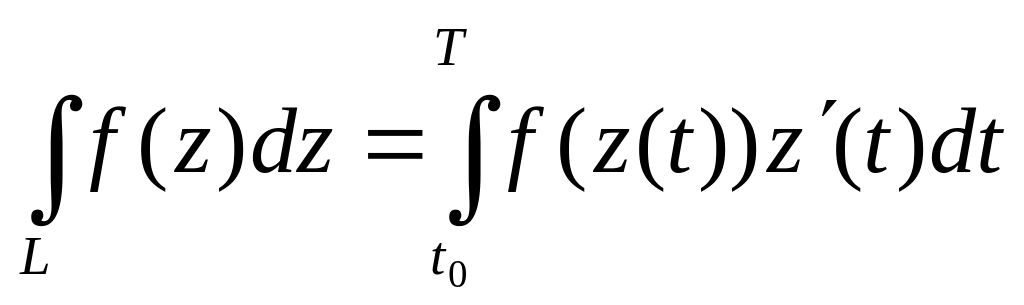Док-во:
По Утв1
;
;
.
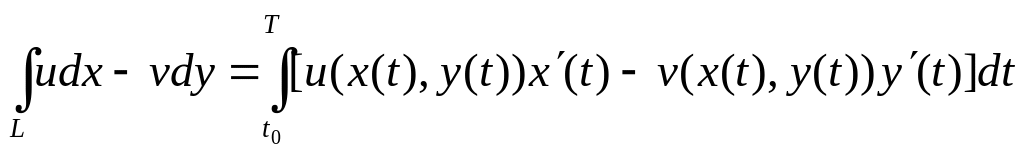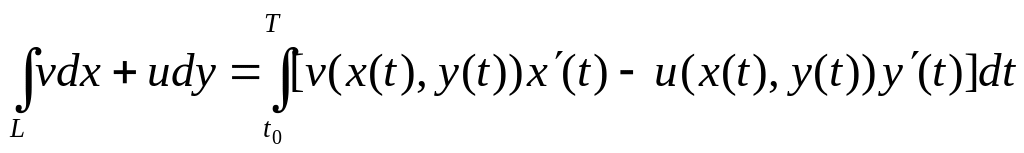Свойства интеграла
1.
2.
3.
4.
,
где -L
– обход дуги L
в обратную сторону.
5. Если
,
то
,
где
-длина
L.
Док-во:
длина
хорды.
Замечание. Криволинейный интеграл существенно зависит от кривой.
Утв.
.
Док-во:
.
След.
Утв.
где
Док-во:
(
)
Основная теорема Коши для односвязаной области
Если G
– односвязная область,
- аналитическая внутри G.
Г – замкнутый контур, лежащий внутри
G,
то
Док-во:
G
Г
Из Утв1. (1)
Из теории криволинейного интеграла известно, что
если
,
(2)
то
(3)
т.к. f – аналитическая, то выполнены условия Коши – Римана:
в
силу (2) и (3) из (1) следует, что
След.
Если дуги
и
соединяют
точки А и В и, при этом дуга
обходится в направлении от А к В, а дуга
обходится в направлении от В к А, то
Док-во:
.
Зам. Для аналитической функции важны лишь начало и конец дуги.
Основная теорема Коши для многосвязной облости
Теорема.
Если G
– многосвязаная область, связанная
некоторыми контурами,
- аналитическая функция в G
и на границе G,
то интеграл по границе области G,
проходимой по следующему правилу: при
прохождении контура непосредственно
примыкающая к нему область должна
находится по левую руку (Г проходится
по часовой стрелке, а
-по
стрелке) равен нул
ю.
G
Док-во:
1) - аналитическая функция на границе, следовательно - аналитическая в каждой точке границы - аналитическая в каждой точке границы и в некоторой ее окрестности. Покроем границу окрестностями ее точек. Т.к. граница – компакт, то можно выделить конечное подпокрытие. Расширим область аналитичности, используя это покрытие граница погружена в область аналитичности.
2) Разрежем область
G
по
-
получим односвязную облость. Граница
области G
и линия разреза(граница новой области)
лежат в области аналитичности функции
.
3)
След. Если
лежит внутри Г,
- аналитическая в области между Г и
и на них, то
Док-во:
Лекция 5