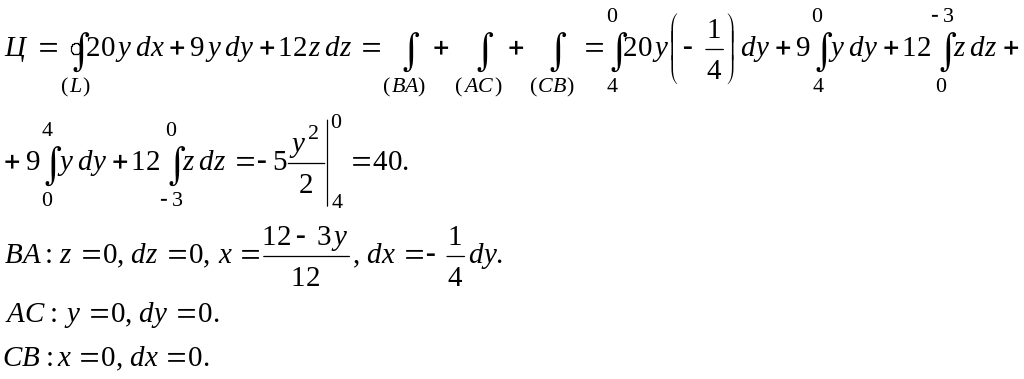Дивергенция.

Рассмотрим в области (V) векторное поле

F(P) = {X(P), Y(P), Z(P)}

Рассмотрим точку Р и вокруг нее замкнутую ориентированную поверхность (S). Ориентированная поверхность – это поверхность, на которой выбрано определенное направление нормали.

Он характеризует силу источников векторных линий в объеме (V), ограниченном поверхностью (S).

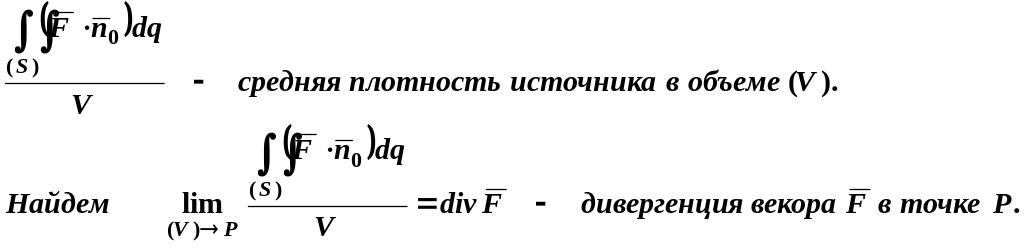
Дивергенция характеризует плотность источника в точке P.

Найдем выражение для дивергенции через координаты векторного поля.

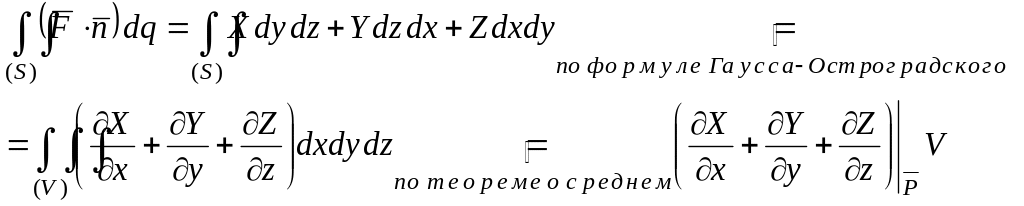
Предполагаем, что функции X, Y, Z непрерывны вместе со своими производными. Тогда

Если P(x, y, z) – произвольная точка, то

d ivF = .

Векторное поле порождает скалярное поле – поле дивергенции.

Формула Гаусса-Остроградского в векторном виде имеет вид

Поток вектора через замкнутую поверхность в направлении внешней нормали равен тройному интегралу от дивергенции векторного поля.

Е сли в области нет ни источников, ни стоков, то , где (S) – любая замкнутая поверхность, и div F ≡ 0.

Е сли div F ≡ 0, то поток через любую замкнутую поверхность (S) равен нулю, и в области нет ни источников, ни стоков. Поле в этом случае называется соленоидальным.

Р ассмотрим соленоидальное поле, т.е. div F = 0, и возьмем векторную трубку, т. е. такую поверхность, которая в каждой точке касается векторного поля. (S₂) n F n . n

F

(S₃)

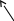
n

(S₁)

Проведем два произвольных сечения векторной трубки (S₁) и (S₂). Рассмотрим поток через замкнутую поверхность трубки (S₃) и сечений (S₁) и (S₂).

.

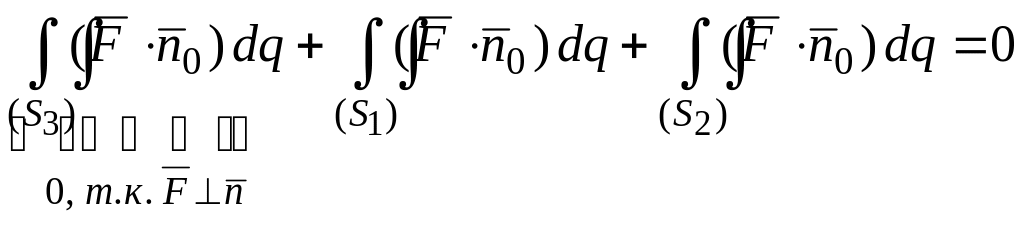На поверхности (S₁) изменим направление нормали. Тогда изменит знак.

Поток через различные сечения векторной трубки сохраняет постоянное значение.

В гидромеханической интерпретации – при отсутствии источников количество жидкости, протекающей через различные сечения векторной трубки, сохраняет постоянное значение.

Циркуляция. Ротор.

Рассмотрим векторное поле

F(P) = X(x,y,z) i + Y(x,y,z) j + Z(x,y,z) k (1)

и замкнутый контур (L).

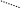F(P) dr

F_s (L)

P

Рассмотрим интеграл

- циркуляция вектора F вдоль замкнутого контура (L).

Дадим другое выражение циркуляции. Рассмотрим вектор dr = {dx, dy, dz}. Тогда

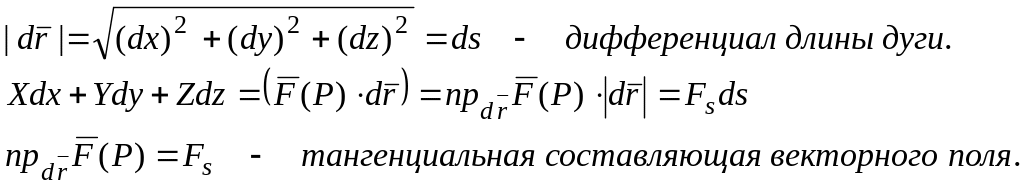
Циркуляция запишется

Ц = .

Физический смысл циркуляции. Если поле силовое, то циркуляция равна работе поля вдоль замкнутого контура (L).

Формула Стокса для контура (L) имеет вид

Здесь (S) – поверхность, натянутая на контур (L).

n₀

(S)

(L)

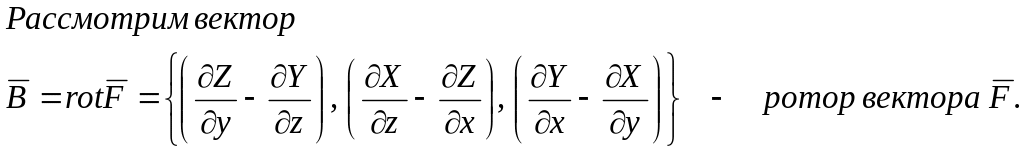
Поле вектора F порождает другое векторное поле – поле ротора.

Формула Стокса в векторном виде запишется

.

П оток ротора через поверхность (S), натянутую на замкнутый контур (L), равен циркуляции вектора F вдоль этого контура.

Направление обхода контура(L) должно быть согласовано с выбранным направлением нормали n₀, Если смотреть с конца вектора n₀, обход контура (L) должен казаться происходящим против часовой стрелки.

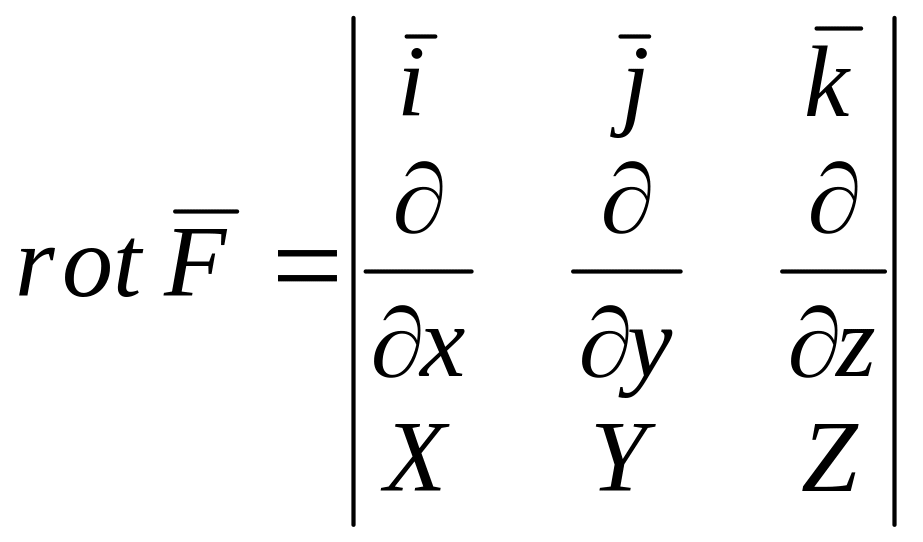
Если для данного векторного поля rot F = 0, то

= 0, но это означает, что существует функция   u = u(x, y, z) такая, что du = X dx + Y dy +Z dz . Отсюда

т.е. поле вектора F является полем градиента.

Функция u(x, y, z) называется потенциалом, а поле вектора F называется потенциальным.

Очевидно, rot grad u = 0.

Примеры.

1. Дана векторная функция F(x, y, z) = 20y i + 9y j + 12z k. Найти поток вектора

   1. через полную поверхность пирамиды, ограниченной плоскостями координат и плоскостью (S) 12x + 3y – 4z -12 = 0 в направлении внешней нормали;

   2. через грань (S).

Р е ш е н и е.

a)

z

k dq

B y γ

A

x dx dy

n₀

C

b)

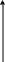
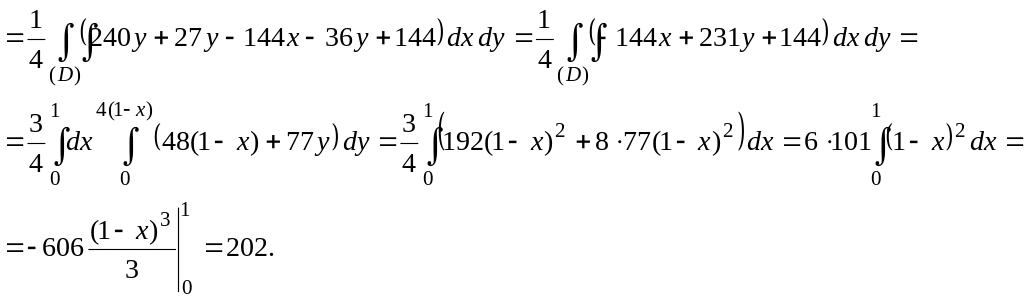
y

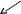y = 4 – 4x

(D)

0 1 x

2. В условиях предыдущей задачи найти циркуляцию векторного поля F(x, y, z) вдоль линии пересечения плоскости (S) с координатными плоскостями двумя способами

   1. по формуле Стокса, приняв в качестве поверхности, по которой производится интегрирование, плоскость треугольника, отсекаемого от плоскости (S) координатными плоскостями, при этом считать нормаль направленной в сторону противоположную началу координат;

   2. непосредственно, по определению циркуляции.

Решение.

a)

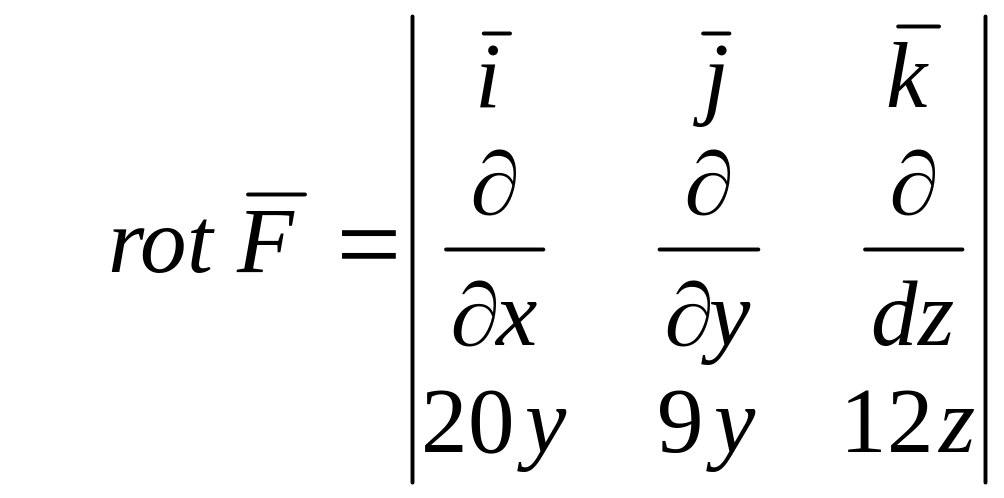= − 20 k.

По формуле Стокса

∙

3. Непосредственно, по определению циркуляции.