1.4. Адсорбция на пористых адсорбентах.

Капиллярная конденсация. Пористые адсорбенты, такие как активированный уголь, цеолит, глины имеют значительно большую удельную поверхность (поверхность, соответствующую 1 г адсорбента), чем непористые. По этой причине максимальное количество молекул адсорбата, способных адсорбироваться на 1 г пористого адсорбента (его емкость) много выше чем у непористого. Кроме общего увеличения адсорбции, на пористых адсорбентах происходит конденсация паров адсорбата внутри пор адсорбента при давлениях значительно меньших чем на непористых. Это связано с уменьшением давления насыщенного пара над вогнутыми менисками жидкости внутри капилляров. Это приводит к еще большей, по сравнению с непористыми адсорбентами, степени адсорбции.

1.5. Адсорбция из растворов.

Согласно теории Лэнгмюра, основные закономерности адсорбции из жидких растворов совпадают с закономерностями адсорбции из газов, с той разницей, что поверхность адсорбента всегда целиком занята молекулами растворителя и растворенного вещества. Если обозначить долю поверхности адсорбента, занятую молекулами растворенного вещества как , а молекулами растворителя как , то скорость адсорбции растворенного вещества, зависящая от числа соударений его молекул с поверхностью адсорбента занятой молекулами растворителя , будет пропорциональна молярной его концентрации. Скорость десорбции будет пропорциональна числу молекул растворенного вещества на единице поверхности адсорбента, то есть . В равновесии скорости адсорбции и десорбции равны, поэтому:

= ,

откуда:

,

где − константа равновесия процесса адсорбции.

Если в растворе находится два растворенных вещества, то отношение степеней их адсорбции зависит как от соотношения их концентраций, так и констант равновесия адсорбции:

где и − степень адсорбции растворенного вещества (1) и (2), соответственно. Чем выше концентрация растворенного вещества и константа равновесия его адсорбции, тем большая доля поверхности занята этим растворенным веществом.

Рассмотрим процесс адсорбции растворенного вещества из водного раствора на поверхности активированного угля. Уголь является неполярным адсорбентом, слабо взаимодействующим с молекулами воды. По этой причине поверхностное натяжение на такой поверхности довольно велико. Любое растворенное вещество, менее полярное чем вода, попадая в поверхностный слой уменьшает поверхностное натяжение, так как энергия взаимодействия его с водой или с другой такой же молекулой меньше энергии взаимодействия молекул воды между собой:

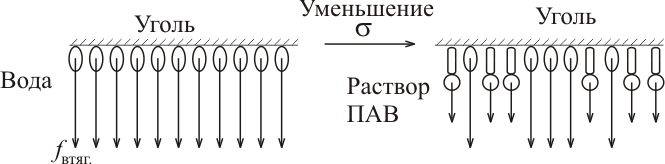
Поскольку при этом уменьшается и энергия Гиббса системы, процесс вытеснения молекул воды с поверхности угля менее полярными молекулами ПАВ, то есть их адсорбция, протекает самопроизвольно. Такие вещества являются поверхностно-активными по отношению к воде. Они накапливается на поверхности угля. Одновременно протекает и их десорбция, степень которой растет с температурой. Величина равновесной адсорбции определяется адсорбционным уравнением Гиббса:

Моль/м2 ,

где С − молярная концентрация растворенного ПАВ; − его поверхностная активность. Для гомологического ряда ПАВ выполняется правило Траубе (см. теоретическое введение). Так, пропионовая кислота СН₃СН₂СООН адсорбируется при одной и той же концентрации примерно втрое в большей степени чем уксусная кислота СН₃СООН, поскольку ее поверхностная активность втрое выше чем у уксусной кислоты. В случае особо мелкопористых адсорбентов правило Траубе не выполняется, поскольку с ростом длины цепочки увеличивается объем молекулы ПАВ и уменьшается число пор, доступных для нее, уменьшается эффективная удельная площадь поверхности адсорбента. В этом случае выполняется так называемое обращенное правило Траубе − чем длиннее цепочка, тем меньше адсорбция.

Адсорбция карбоновой кислоты на поверхность активированного угля из неполярного растворителя, например бензола, не происходит, поскольку молекулы карбоновой кислоты являются более полярными чем молекулы бензола. Поэтому, попадая в поверхностный слой они увеличивают поверхностное натяжение, то есть энергию системы. Такой процесс самопроизвольно происходить не может. Карбоновая кислота по отношению к бензолу оказывается поверхностно-инактивным веществом и не адсорбируется на поверхности раздела. По этой же причине из водного раствора на поверхности активированного угля не адсорбируются ионы электролитов, взаимодействующие между собой и с молекулами воды с энергией большей, чем молекулы воды между собой.

Как показано ранее, зависимость степени адсорбции от концентрации растворенного вещества описывается уравнением Лэнгмюра:

Поскольку , где − максимальная адсорбция Гиббса, то:

Так как определение удельной площади поверхности адсорбента весьма затруднено, на практике часто пользуются величиной адсорбции не на единице поверхности адсорбента, а на единице его массы. В этом случае степень адсорбции выражают в молях адсорбата на единицу массы адсорбента (х/m) молей/г и уравнение Лэнгмюра приобретает вид:

Г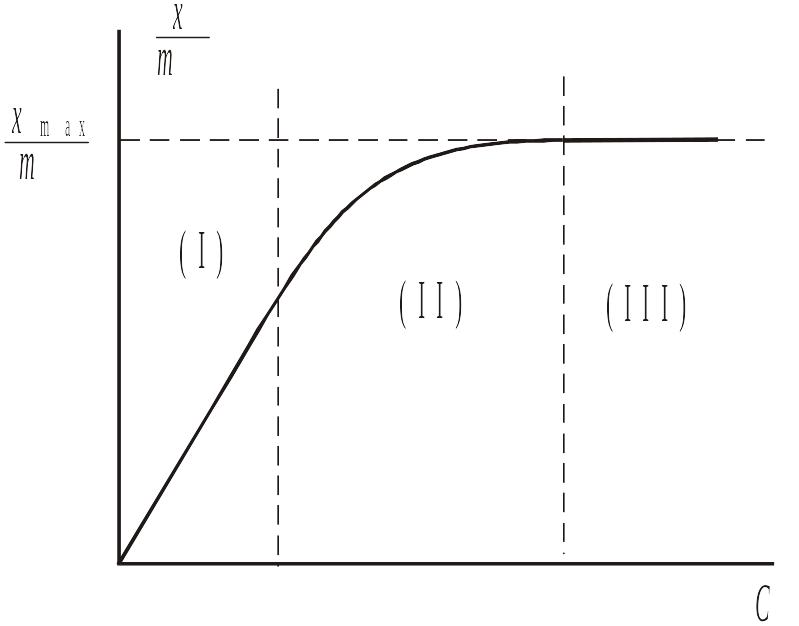 рафик зависимости степени адсорбции от концентрации растворенного ПАВ может быть условно разбит на три части. При малых концентрациях ПАВ, то есть при зависимость является линейной (I). В этой области концентраций ПАВ поверхность адсорбента занята в основном молекулами растворителя. И наоборот, при достаточно высокой концентрации ПАВ, при вся поверхность адсорбента занята молекулами ПАВ, степень адсорбции равна максимальной и не зависит от концентрации ПАВ (III). В промежуточной области, при зависимость величины адсорбции от концентрации ПАВ является нелинейной (II).

Как и в случае адсорбции газов, увеличение температуры приводит к росту скорости десорбции и соответствующему уменьшению степени адсорбции при данной равновесной концентрации ПАВ. Величина максимальной адсорбции определяется величиной удельной поверхности адсорбента и размерами молекул адсорбата, поэтому не зависит от температуры.

Нелинейный участок изотермы адсорбции описывается эмпирическим уравнением Фрейндлиха:

,

г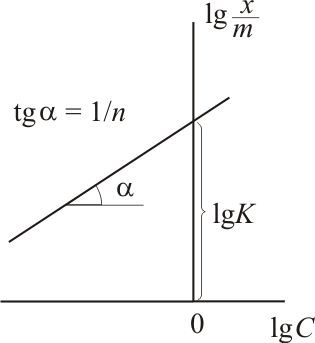 де величина константы К зависит от условий адсорбции, свойств адсорбента (от его удельной поверхности), размеров молекул адсорбата, а величина константы 1/n составляет 0.3–0.5. Для конкретных условий адсорбции константы уравнения Фрейндлиха легко могут быть найдены путем измерения степени адсорбции при нескольких равновесных концентрациях ПАВ. Логарифмирование уравнения Фрейндлиха приводит к уравнению прямой в координатах − :

.

Построив соответствующий график, по величине отсекаемого отрезка, равного , можно найти константу К, а тангенс угла наклона графика дает величину 1/n.

1.6. Ход работы и обработка полученных данных.

Приготовление исходных растворов уксусной кислоты.

1.6.1. В пять нумерованных колб с помощью мерной колбы налить по 100 мл дистиллированной воды.

1.6.2. С помощью мерной колбы налить в колбу № 1 100 мл исходного (по заданию) раствора с концентрацией уксусной кислоты , сполоснуть мерную колбу образовавшимся раствором с концентрацией уксусной кислоты равной , вылить его обратно в колбу № 1.

1.6.3. С помощью мерной колбы 100 мл раствора из колбы № 1 вылить в колбу № 2, ополоснуть мерную колбу образовавшимся раствором, вылить обратно в колбу № 2.

1.6.4. Аналогично 100 мл раствора из колбы № 2 с помощью мерной колбы перелить в колбу № 3 и т.д. Из колбы № 5 лишние 100 мл раствора вылить в раковину.

Проведение адсорбции уксусной кислоты на активированном угле.

1.6.5. На технических весах взять пять навесок по 2.00±0.01 г активированного угля (m), всыпать их в колбы № 1 − № 5, записать время.

1.6.6. В течение ~30 минут поочередно встряхивать колбы для ускорения установления равновесия адсорбции.

1.6.7. По истечении ~30 минут профильтровать растворы из колб № 1 − № 5 через складчатые фильтры в соответствующие пронумерованные колбы, отбросив в каждом случае небольшую порцию фильтрата.

Определение исходных и равновесных концентраций растворов уксусной кислоты.

1.6.8. Путем потенциометрического титрования раствором щелочи известной концентрации (см. инструкцию на рабочем месте) определить равновесную концентрацию уксусной кислоты в каждом из пяти фильтратов ( ). Для каждого фильтрата провести три параллельных титрования, взять среднее арифметическое, заполнить табл. 1.

1.6.9. Аналогично определить концентрацию исходного раствора уксусной кислоты ( ), вычислить исходные концентрации растворов в колбах № 1 − № 5: и т.д., внести полученные данные в табл. 2.

Определение констант уравнения Фрейндлиха.

1.6.10. Вычислить исходные и равновесные , ммоль, содержания уксусной кислоты в 100 мл раствора, а также равновесные величины адсорбции , ммоль/г, заполнить табл. 2.

1.6.11. Построить графики зависимости степени адсорбции от равновесной концентрации уксусной кислоты в координатах и .

1.6.12. Графически определить коэффициенты уравнения Фрейндлиха − К и .

Таблица 1.

№ раствора	Объем раствора на титрование, мл	Эквивалентный объем титранта (NaOH), мл			Норм. титранта, г-экв/л	, г-экв/л
		1	2	Средн.
1 2 …. 5

Таблица 2.

№ раствора	Конц. уксусной кислоты, г-экв./л		Содерж. уксусной к-ты в 100 мл. раствора, ммоль		, ммоль/г	lg Ci,равн.	lg (x/m).
1 2 …. 5

Контрольные вопросы

1. Виды межмолекулярного взаимодействия. Энергия притяжения и отталкивания, потенциальная кривая взаимодействия двух частиц, зависимость энергии взаимодействия от структуры частиц.

2. Поверхностное натяжение на границе раздела фаз. Причина возникновения, влияние различных факторов на величину поверхностного натяжения.

3. Мономолекулярная и полимолекулярная адсорбция на твердой поверхности. ПАВ и ПИАВ, влияние различных факторов на степень адсорбции. Уравнение Лэнгмюра, уравнение Фрейндлиха.

4. Нахождение констант уравнения Фрейндлиха для адсорбции карбоновой кислоты из водного раствора на поверхности активированного угля.

Литература

1. Герасимов Я.И., Древиг В.П., Еремин Е.Н. и др. Курс физической химии. Том I. –М: ГХИ, 1963. С. 435 – 455, 513 – 542.

2. Григоров О.Н. и др. Руководство к практическим работам по коллоидной химии. –М., –Л.: Химия, 1964. С. 86 – 92, 107 – 120.

3. Воюцкий С.С. Курс коллоидной химии. –М.: Химия, 1976. С. 81 – 99, 137 – 145.

РАБОТА № 8

ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ РАСТВОРОВ ПАВ И АДСОРБЦИИ ИХ НА ГРАНИЦЕ РАЗДЕЛА ЖИДКОСТЬ – ГАЗ ОТ КОНЦЕНТРАЦИИ ПАВ

1. Теоретическая часть

1.1. Адсорбция растворенных веществ на поверхности раздела жидкость – газ. Изотерма адсорбции, зависимость поверхностного натяжения раствора от концентрации ПИВ и ПИАВ.

При постоянной температуре и постоянном давлении энергия гетерогенной системы из двух фаз, разделенных поверхностью раздела, складывается из энергии Гиббса фаз (I) и (II), а также избыточной энергии Гиббса поверхности раздела:

Соответственно, изменение энергии такой системы также является суммой:

.

Самопроизвольными являются все процессы, приводящие к уменьшению энергии Гиббса системы (dG < 0), При постоянстве энергий Гиббса фаз ( ) такими процессами являются процессы, ведущие либо к уменьшению площади поверхности раздела ( , так капля ртути самопроизвольно принимает форму шара, имеющего наименьшую поверхность при данном объеме), либо к уменьшению поверхностного натяжения при постоянной величине поверхности раздела ( ). Поскольку наличие ПАВ в поверхностном слое приводит к уменьшению поверхностного натяжения, процесс увеличения его концентрации на поверхности раздела по сравнению с концентрацией в объеме является термодинамически выгодным и самопроизвольным.

Процесс концентрирования, или сгущения растворенного вещества на поверхности раздела фаз называется адсорбцией. Этот процесс сопровождается уменьшением энергии системы за счет уменьшения избыточной энергии поверхности раздела фаз. При отсутствии теплового движения и, соответственно, диффузии, растворенное вещество заполняло бы всю поверхность раздела фаз. Процесс адсорбции, однако, всегда сопровождается процессом десорбции, обусловленным диффузией ПАВ с поверхности раздела в объем фазы. При данной концентрации ПАВ и температуре устанавливается равновесие между адсорбцией и десорбцией. Рост концентрации ПАВ в растворе увеличивает скорость адсорбции, увеличение температуры системы увеличивает скорость десорбции. Соответственно этому, с ростом концентрации ПАВ в растворе степень его адсорбции на поверхности растет, а с ростом температуры – уменьшается.

Величину степени адсорбции легко вычислить по уравнению Гиббса, из которого следует, что с ростом концентрации ПАВ и его поверхностной активности степень адсорбции увеличивается, а с ростом температуры – уменьшается:

Аналогичная зависимость степени адсорбции ПАВ от его концентрации выражается уравнением изотермы адсорбции Лэнгмюра:

,

где Г_∞ – максимальное количество молей ПАВ, способное адсорби­роваться на единице площади поверхности раздела; К – константа равновесия адсорбции, зависящая от теплоты адсорбции и, соответственно, от поверхностной активности ПАВ и температуры. Величина Г_∞ не зависит от температуры и определяется лишь эффективным сечением молекулы ПАВ (чем больше сечение, тем меньше молекул может поместиться на единице площади поверхности раздела, тем меньше Г_∞).

Графики изотерм адсорбции имеют следующий вид:

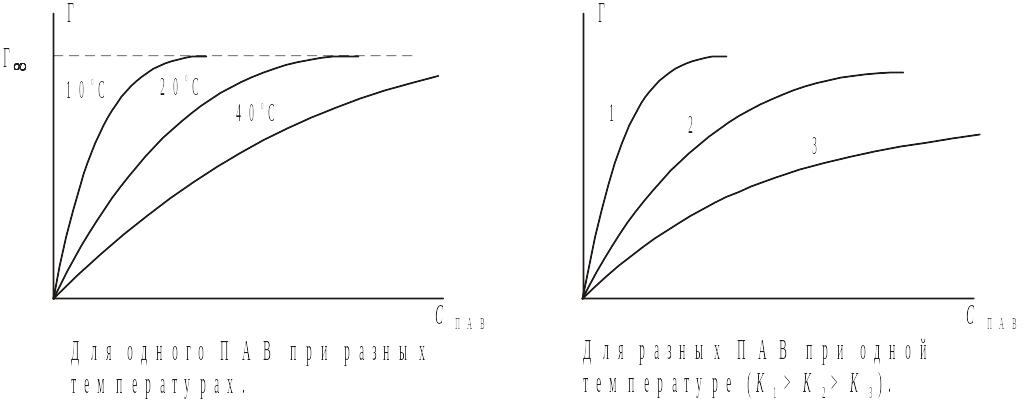
В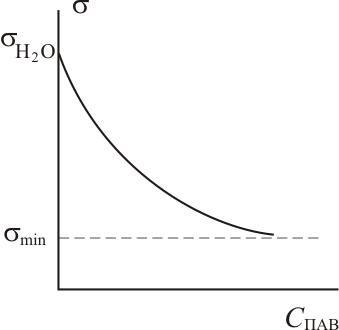 соответствии с ростом содержания молекул ПАВ в поверхностном слое, то есть с увеличением Г, поверхностное натяжение на границе раздела фаз уменьшается. При максимальной адсорбции Г_∞ , на поверхности раздела образуется мономолекулярный слой молекул ПАВ, причем полярными, гидрофильными группами они обращены к жидкой фазе, а гидрофобными – к газовой фазе. Величина поверхностного натяжения принимает минимальное значение , соответствующее поверхностному натяжению мономолекулярного слоя ПАВ. Математически зависимость σ от концентрации ПАВ выражается уравнением Шишковского:

,

где В – коэффициент, определяемый геометрическими размерами молекулы ПАВ и не зависящий от его поверхностной активности; К – константа равновесия адсорбции.

Величина максимальной адсорбции Г_∞ легко находится графическим способом из уравнения изотермы адсорбции. Действительно, из уравнения Лэнгмюра следует, что

.

Если умножить обе части этого равенства на концентрацию ПАВ оказывается, что зависимость С/Г от С является линейной:

.

И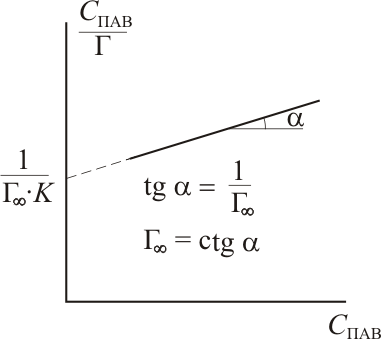 спользуя экспериментальные данные строят график в координатах С_ПАВ/Г – С_ПАВ, из наклона которого определяют Г_∞, а из отсекаемого отрезка – величину константы равновесия адсорбции.

Поскольку при предельной адсорбции Г_∞ число молей ПАВ в адсорбционном слое, соответствующем 1 м² поверхности раздела много больше соответствующей величины в том же объеме внутри фазы (n^S>>n), то Г_∞ = n^S – n = n^S. Следовательно, число молекул ПАВ на единице площади поверхности раздела фаз при максимальной адсорбции составляет n^S·N_A = Г_∞·N_A , где N_A = 6.02·10²³ 1/моль – число Авогадро. Площадь сечения одной молекулы ПАВ, определяемая размером полярной группы, погруженной в жидкую фазу, составляет:

, м² .

Объем адсорбционного слоя, соответствующий 1 м² поверхности раздела можно вычислить как произведение площади на толщину слоя, равную эффективной длине молекулы ПАВ. Его масса равна произведению объема на плотность ПАВ: . В то же время масса поверхностного слоя ПАВ на 1 м² поверхности раздела равна произведению массы одного моля ПАВ (ММ_ПАВ) на число молей ПАВ на 1 м² поверхности раздела при предельной адсорбции (n^S = Г_∞): . Следовательно:

, откуда , м.

Таким образом, определив предельную адсорбцию можно вычислить геометрические параметры молекулы ПАВ – ее длину и площадь поперечного сечения.

В то время как ПАВ уменьшают поверхностное натяжение на поверхности раздела фаз, ПИАВ либо не влияют на величину поверхностного натяжения, либо слабо ее повышают. Зависимость величины от концентрации ПАВ в растворе является линейной:

.

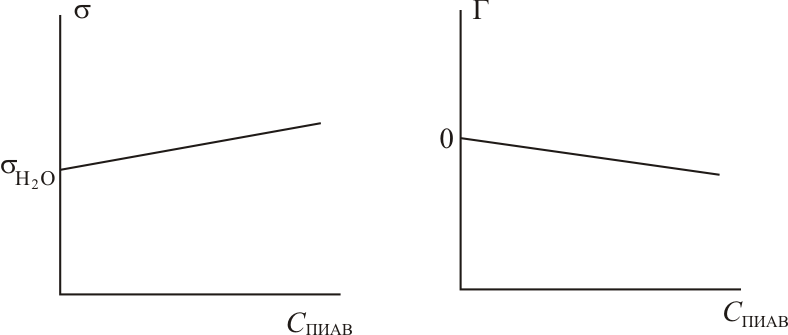
Величина поверхностной активности ПИАВ является отрицательной. Отрицательной является и величина адсорбции. Графики зависимости и Г от концентрации ПИАВ имеют вид:

1.3. Измерение поверхностного натяжения на границе раздела "жидкость – газ".

1.3.1. Метод капиллярного поднятия.

П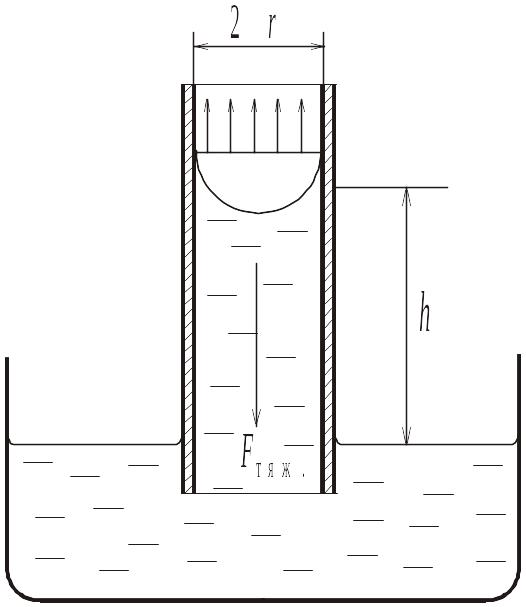 ри идеальном смачивании материала капилляра жидкосью, сила, втягивающая столб жидкости в капилляр, равна произведению поверхностного натяжения (сила, приходящаяся на единицу длины контура поверхности раздела) на длину окружности мениска жидкости:

.

В равновесии эта сила уравновешена силой тяжести столба жидкости:

.

Таким образом: , откуда:

,

где – константа капилляра, h – высота поднятия, а ρ – плотность жидкости. Константу капилляра легко найти, измерив высоту поднятия и плотность жидкости с точно известной величиной поверхностного натяжения (чаще всего дистиллированной воды):

.
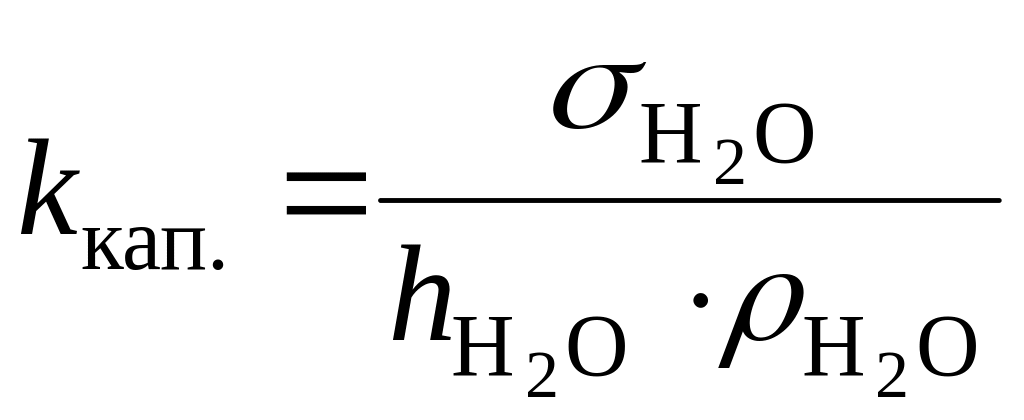