В дискретных рядах:
а)
если всем единицам ряда придать порядковые
номера, то в
ряду с нечетным числом членов
медианой будет являться значение
признака с номером (
):
;
(1.16)
б) если в ряду четное число членов, то медианой будет являться среднее арифметическое из 2-х значений ряда:
.
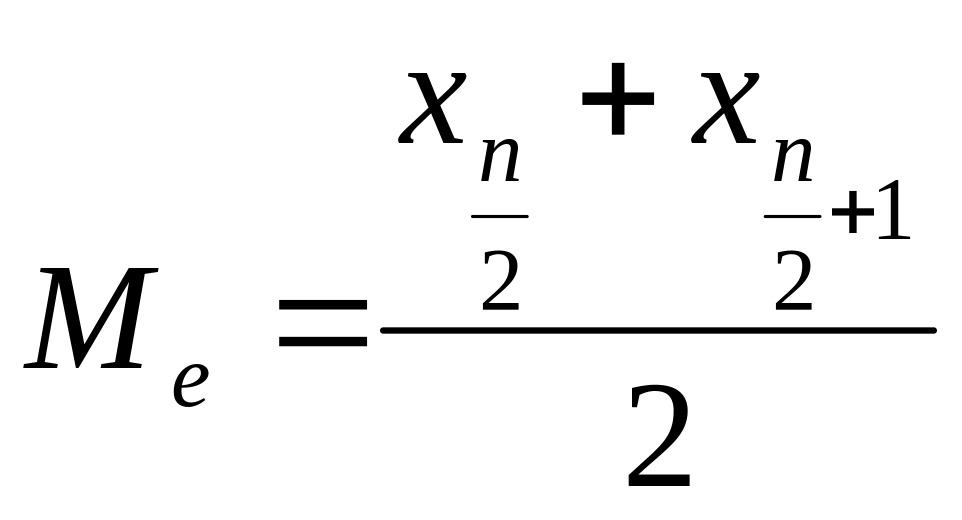(1.17)
Однако,
при
разница в значениях 2-х смежных вариантов
невелика и медианой может считаться
значение признака с номером (
):
.
(1.18)
В интервальных рядах. Для нахождения медианы, предварительно необходимо определить интервал, в котором находится медиана. Этот интервал характерен тем, что его кумулятивная частота (накопленная) равна или больше полу суммы всех частот ряда:
.
(1.19)
-
Границы интервалов
Вес, частота,
Кумулятивная частота,
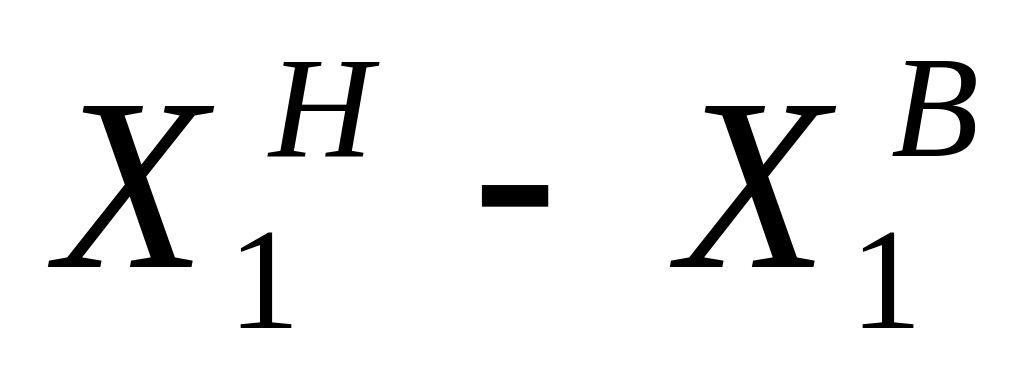
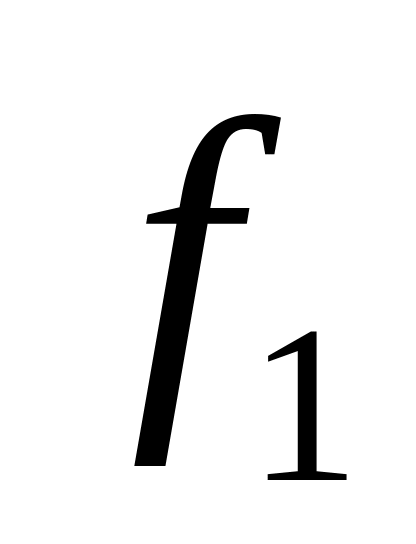
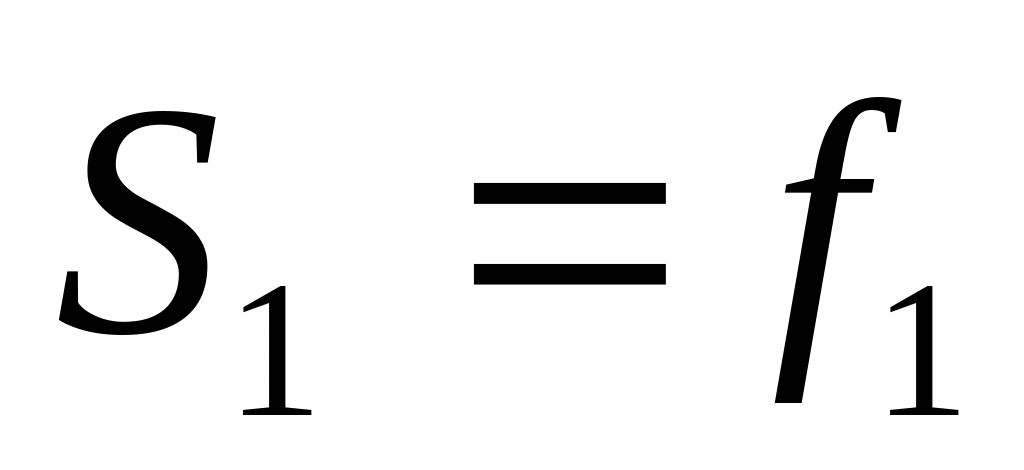
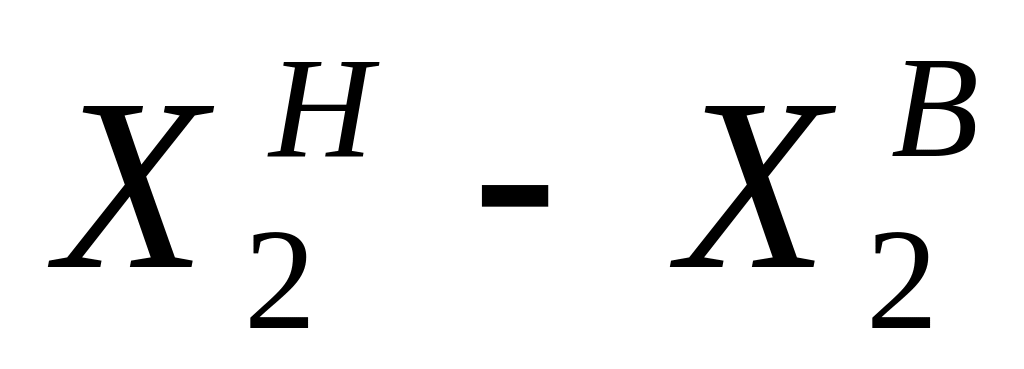
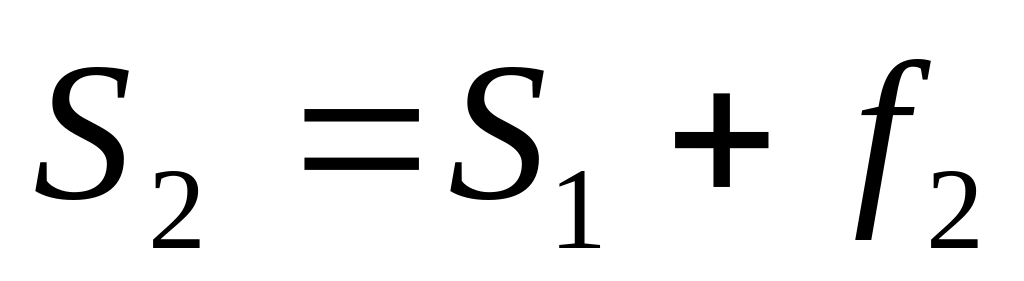
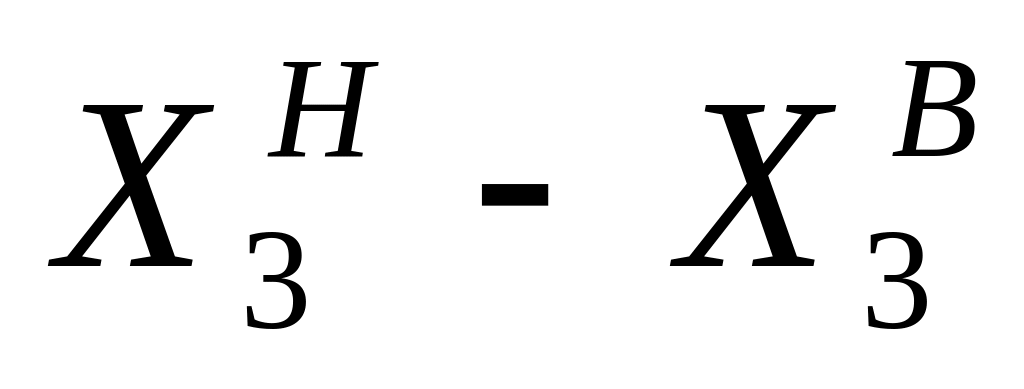
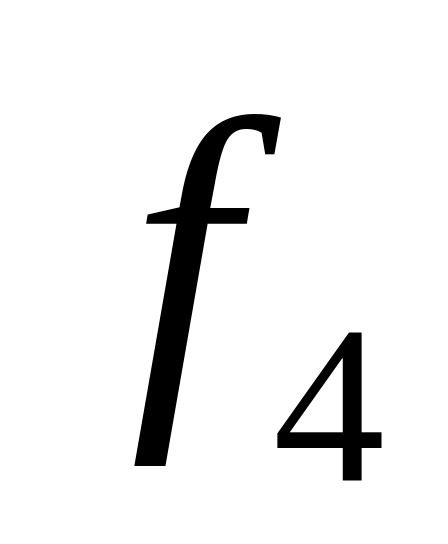
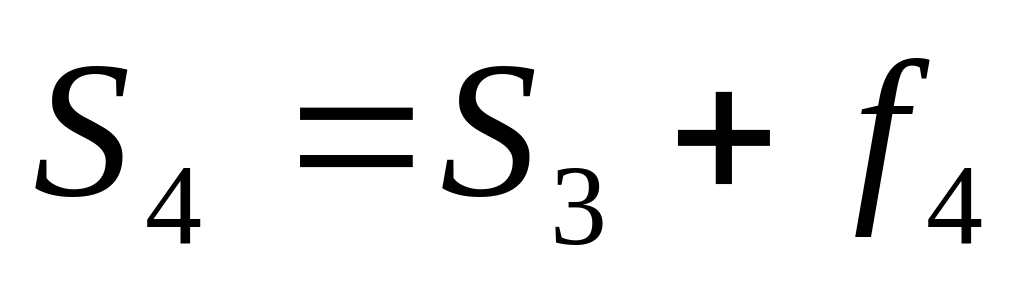
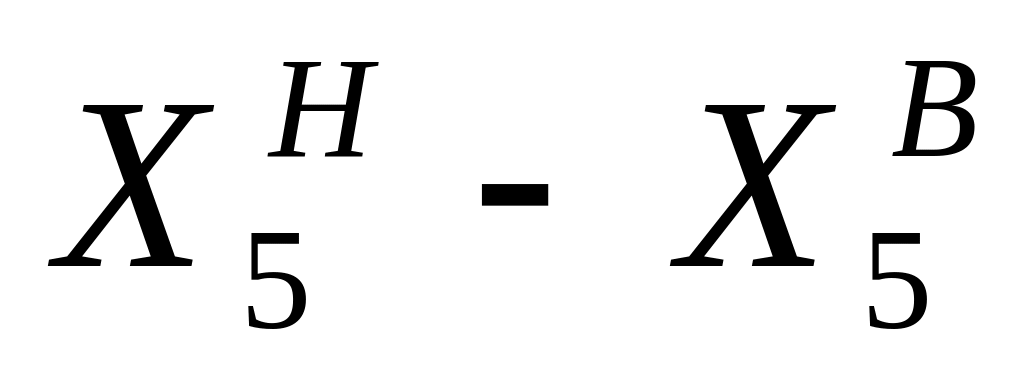
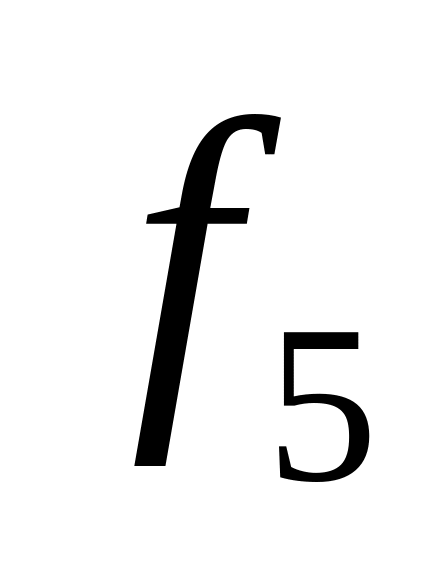
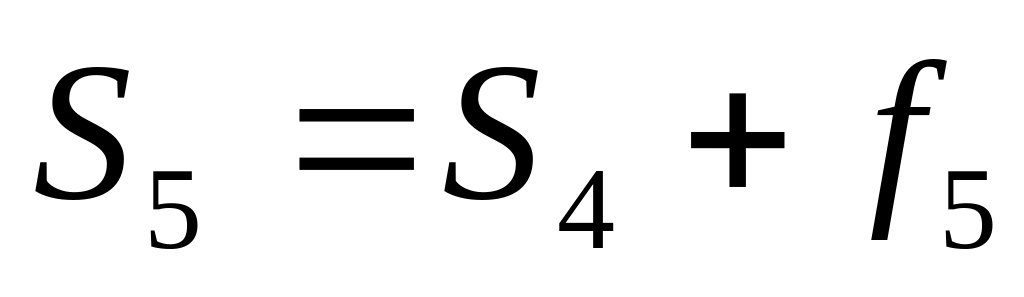
Итого
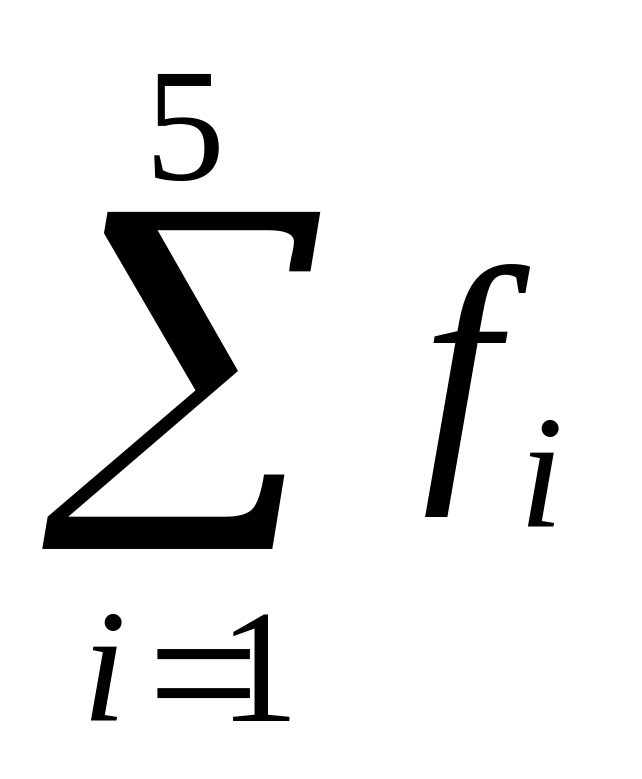
Как только найден медианный интервал, приступают к нахождению медианы:
,
(1.20)
- нижняя граница
медианного интервала;
- размер медианного
интервала;
- кумулятивная
частота предмедианного интервала;
- частота медианного
интервала:
.
(1.21)
Наряду с медианой для более полной характеристики структуры изучаемой совокупности используют и другие значения вариантов, которые занимают в ранжированном ряду вполне определенное положение. К ним относятся квартили и децили.
Квартили (три) делят ряд по сумме на 4 равные части, а децили (девять) на 10.
Мода – величина признака, которая чаще всего встречается в совокупности.
Нахождение моды в вариационных рядах:
В дискретных рядах мода определяется по наибольшей частоте (вариант, обладающий наибольшей частотой, называют модой).
Т.е.
если
max,
где
l=1
,
то
.
В интервальных рядах предварительно необходимо найти интервал, в котором находится мода (модальный интервал).
Модальным интервалом является тот интервал, который обладает наибольшей частотой. (Если есть 2 одинаковые частоты, можно принять любой интервал).
После нахождения модального интервала, мода рассчитывается по следующей формуле:
,
(1.22)
- частота модального
интервала;
-
частота интервала
предшествующего
модальному;
-
частота после модального
интервала;
- нижняя граница
модального интервала;
- размер модального
интервала.
Медиана и мода в отличие от средней арифметической не погашают индивидуальных различий в значениях варьирующего признака, и потому являются очень важными характеристиками статистической совокупности. Соотношение этих трех показателей позволяет, достаточно исчерпывающим образом, охарактеризовать распределение признака в совокупности.