
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ –
ВЫСШАЯ ШКОЛА ЭКОНОМИКИ
САНКТ-ПЕТЕРБУРГСКИЙ ФИЛИАЛ
О.В. Панневиц, А.С. Рыбакин
Математический анализ
(примеры и задачи)
Учебно-методическое пособие
Санкт-Петербург
2010 г
Панневиц О.В., Рыбакин А.С.
Математический анализ (примеры и задачи). Учебно-методическое пособие. – Издательство «», 2010. – 101 с.
Пособие соответствует программе дисциплины «Математический анализ» экономических специальностей. Весь материал разбит на практические занятия по отдельным темам. При этом каждое занятие состоит из четырех пунктов:
1 – повторение основных определений, теорем и рабочих формул по теме занятия;
2 – примеры с решениями различных типов задач и примеров;
3 – набор задач и примеров, которые рекомендуется решить (как правило, самостоятельно в аудитории);
4 – набор задач и примеров для самостоятельного решения (домашнее задание).
Такая структура позволяет наиболее эффективно использовать время занятия как студентам, так и преподавателю.
Кроме того, студент может самостоятельно отработать указанную тему (при необходимости).
Для студентов и слушателей программ высшего профессионального образования.
Рекомендовано к печати Учебно-методическим советом СПб филиала ГУ-ВШЭ в качестве учебного пособия.
Оглавление
Практическое занятие №1. Функции…………………………………………………………………….4
Практическое занятие №2.Множества. Операции над множествами………………………………..12
Практическое занятие №3.Предел функции…………………………………………………………...22
Практическое занятие №4.Предел функции (продолжение)………………………………………….25
Практическое занятие №5.Непрерывность функции. Классификация точек разрыва……………...27
Практическое занятие №6.Производные……………………………………………………………....30
Практическое занятие №7.Дифференцирование функций……………………………………………33
Практическое занятие №8.Правило Лопиталя. Касательная и нормаль к плоской кривой………...37
Практическое занятие №9.Монотонность и экстремумы функций…………………………………..40
Практическое занятие №10.Выпуклость и вогнутость кривой. Точки перегиба. Асимптоты кривой. Построение кривой по ее уравнению в явном виде…………………………………………………...43
Практическое занятие №11.Непосредственное интегрирование…………………………………….47
Практическое занятие №12.Метод замены переменной (подстановки)……………………………..48
Практическое занятие №13.Интегрирование по частям………………………………………………50
Практическое занятие №14.Интегрирование рациональных функций………………………………52
Практическое занятие №15.Интегрирование тригонометрических функций, рациональных относительно синуса и косинуса………………………………………………………………………..57
Практическое занятие №16.Определенный интеграл…………………………………………………61
Практическое занятие №17.Определенный интеграл (продолжение)………………………………..64
Практическое занятие №18.Несобственные интегралы……………………………………………….67
Практическое занятие №19.Положительные ряды…………………………………………………….68
Практическое занятие №20.Знакочередующиеся ряды. Знакопеременные ряды (общий случай)…72
Практическое занятие №21.Степенные ряды…………………………………………………………..74
Практическое занятие №22.Ряды Тейлора и Маклорена………………………………………………77
Практическое занятие №23.Ряды Фурье………………………………………………………………..81
Практическое занятие №24.Ряды Фурье (продолжение)………………………………………………86
Практическое занятие №25.Функции нескольких переменных…………………………………….…89
Практическое занятие №26.Функции нескольких переменных (продолжение)……………………..92
Практическое занятие №27.Скалярное поле……………………………………………………………95
Практическое занятие №28.Градиент скалярного поля…………………………………………….….99
Практическое занятие №29.Экстремумы функции нескольких переменных…………………….…101
Практическое занятие №30.Двойной интеграл………………………………………………………..103
Литература……………………………………………………………………………………………….106
Практическое занятие №1.
Функции.
Контрольные вопросы.
1. Дайте определение числовой функции.
2. Что называют областью определения функции и множеством значений?
3. Какие способы задания функции вы знаете?
4. Дайте определение четной, нечетной функции и функции общего вида.
5. Перечислите основные элементарные функции.
Примеры с решениями:
Найти область определения функций:
 ;
;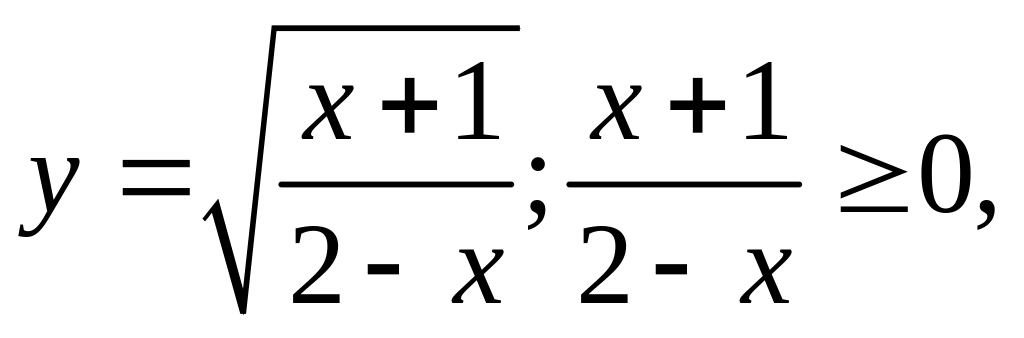


 -
+ -
-
+ -
-1 2
![]() ;
;
 ;
;
Найти множество Y, на которое данная функция отображает множество X:
 - функция,
возрастающая на всей области определения
- функция,
возрастающая на всей области определения
![]() .
.
 - функция убывает
до
- функция убывает
до
 ,
затем возрастает, поэтому считаем
значение в трех точках
,
затем возрастает, поэтому считаем
значение в трех точках
![]()
 - функция,
возрастающая на всей области определения
- функция,
возрастающая на всей области определения
![]() ;
;
 - функция, убывающая
на всей области определения
- функция, убывающая
на всей области определения
![]()
 - функция убывает
на заданной области
- функция убывает
на заданной области
![]()
Определить, является функция четной, нечетной или функцией общего вида:
 - четная;
- четная; - общего вида;
- общего вида; - нечетная.
- нечетная.
4) Построить графики следующих элементарных функций:

 - линейная функция
- линейная функция

-3

-3

 - квадратичная
функция, графиком является парабола
- квадратичная
функция, графиком является парабола


 2
2
-1


 - дробно-линейная
функция, графиком является гипербола
- дробно-линейная
функция, графиком является гипербола


 -1
-1
-1/2

 - логарифмическая
функция
- логарифмическая
функция



-3

 - показательная
функция
- показательная
функция

-1
Примеры для практических занятий:
Найти область определения функции:
 ;
; ;
; ;
; .
.
Найти множество Y, на которое данная функция отображает множество X:


 ;
; .
.
Определить, является функция четной, нечетной или функцией общего вида:
Построить графики следующих функций:

 ;
; ;
; ;
;
Ответы:
1.
 2.
2.
 3.
3.
 4.
4.

1.
 2.
2.
 3.
3.
 4.
4.

1. Четная; 2. Нечетная; 3. Четная; 4. Общего вида.
1

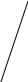 .
.
4
-2
2
 .
.

-3
3

 .
.

 3
3
1 2


4
 .
.
2

 3
3
5 .
.


-2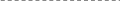
Примеры для самостоятельного решения:
Найти область определения функции:
Найти множество Y, на которое данная функция отображает множество X:
Определить, является функция четной, нечетной или функцией общего вида:
Построить графики следующих функций:
Ответы:
1. 2.
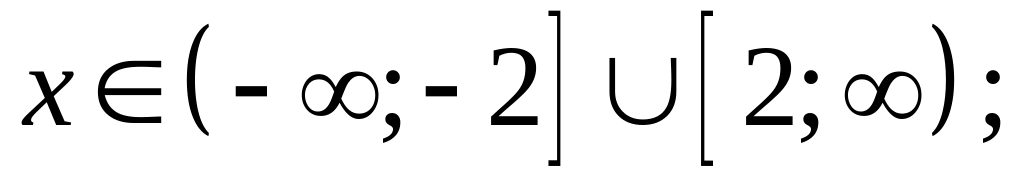 3.
3.
 4.
4.
 5.
5.

1.
 2.
2.
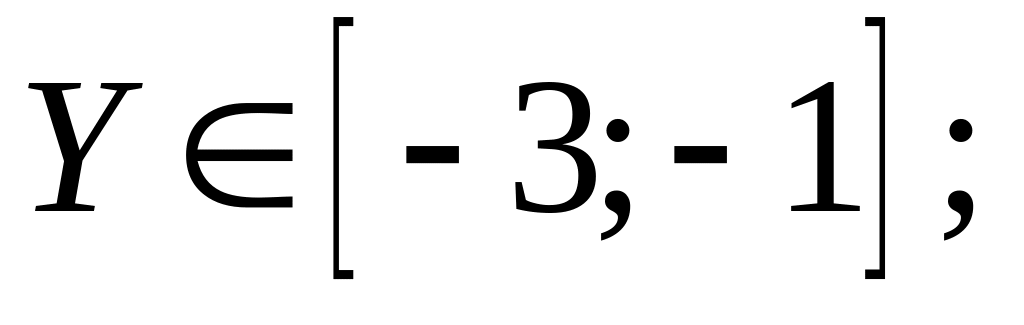 3.
3.
 4.
4.

1. Четная; 2. Нечетная; 3. Четная; 4. Функция общего вида.
1
 .
.

2

2.


 2
2

-3
3.


-2
4 .

-4

5.

 4
4
Практическое занятие №2.
Множества. Операции над множествами.
Контрольные вопросы.
Что понимают под множеством?
Дайте определение подмножества.
Перечислите основные способы задания множеств.
Какое множество называют счетным?
Перечислите основные операции над множествами.
Примеры с решениями:
Заданы два множества
 и
и
 .
.
Найти
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Заданы два множества
 и
и
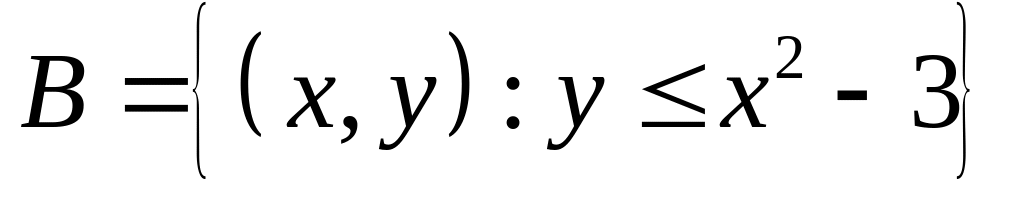
И зобразить
на плоскости
зобразить
на плоскости
![]()
![]()





![]()

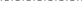

 2
2
 -2
-2
 -3
-3











Заданы два множества
 и
и

Изобразить на
плоскости
![]() .
.







 2
2


1








Заданы три множества
 ,
,
 и
и
![]() .
Изобразить на плоскости
.
Изобразить на плоскости
![]() .
.


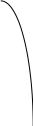



 4
4

1
-2 2
-1
![]()
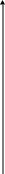




![]()


-2

 -3
-3







Заданы три множества
 ,
,
 и
и
![]() .Изобразить
на плоскости
.Изобразить
на плоскости
![]() .
.

![]()



1






![]()

 1
1

2

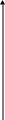





Заданы три множества
 ,
,
 и
и
![]() .
Изобразить на плоскости
.
Изобразить на плоскости
![]() .
.



![]()
 5
5


1 2 3
 -1
-1
-1
-1
![]()




1
 -1
-1




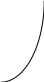
Заданы три множества
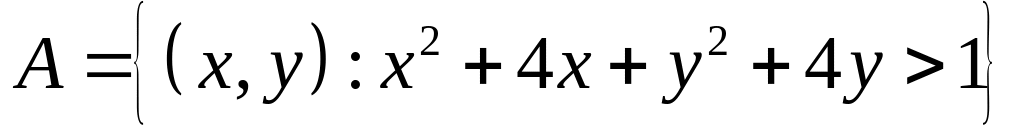 ,
,
 и
и
![]() .Изобразить
на плоскости
.Изобразить
на плоскости
![]() .
.
![]()

 -2
-2
-2

![]()


1
-1 1

-1
![]()






Примеры для практических занятий:
 ,
, ;
;

Изобразить на плоскости:
Ответы:
8)
![]()
9 )





 2
2

1 0)




11)





1 2)




1 3)




1





 4)
4)
Примеры для самостоятельного решения:
Изобразить на плоскости:
Ответы:
1 5)
5)



-2
1

 6)
6)


17)








18)







1


 9)
9)



20)









Практическое занятие №3.
Предел функции.
Контрольные вопросы.
Что называют пределом функции?
Что называют односторонним пределом?
Перечислите типы неопределенностей.
Примеры с решениями:
1. Неопределенность
типа
![]() решаем разбиением на множители
решаем разбиением на множители
 ;
;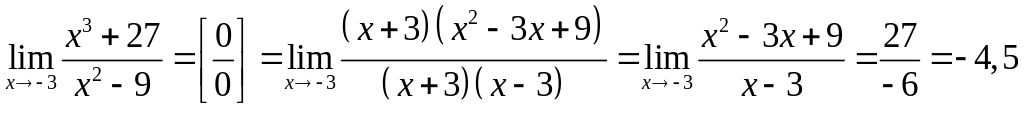 ;
; ;
; ;
;
или домножением на сопряженное
 ;
; ;
;

 ;
;
2. При следующем
типе неопределенности
![]() возможны два способа решения.
возможны два способа решения.
Первый способ (выносим за скобку наиболее быстро растущую степень):
 ;
;
Второй способ (оставляем наибольшую степень):
 ;
;
3. При неопределенности
типа
![]() приводим к общему знаменателю
приводим к общему знаменателю
 ;
; ;
;
или домножаем на сопряженное
 ;
; .
.
Примеры для практических занятий:
14)
![]() ;
15)
;
15)
![]() ;
16)
;
16)
![]() ;
17)
;
17)
![]() ;
18)
;
18)
![]() ;
;
19)
 ;
20)
;
20)
![]() ;
21)
;
21)
 ;
22)
;
22)
![]() ;
;
23)
![]() ;
24)
;
24)
![]() ;
25)
;
25)
![]() ;
26)
;
26)
![]() ;
;
27)
 ;
28)
;
28)
 ;
29)
;
29)
![]() ;
30)
;
30)
![]() ;
;
31)
 ;
32)
;
32)
![]() ;
33)
;
33)
 ;
;
34)
![]() ;
35)
;
35)
![]() .
.
Ответы:
0; 15) 0,7; 16)
 ;
17)
;
17)
 ;
18)
;
18)
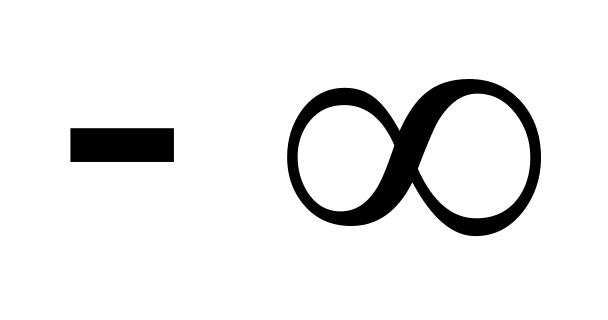 ;
19) 6; 20) 0; 21)
;
19) 6; 20) 0; 21)
 ;
22)
;
22)
 ;
23)
;
23)
 ;
24)
;
24)
 ;
;
25)
![]() ;
26) 0; 27) –2; 28) 1,5; 29) 0; 30)
;
31) 0,4; 32) 0; 33) 0,25; 34) 2; 35)
.
;
26) 0; 27) –2; 28) 1,5; 29) 0; 30)
;
31) 0,4; 32) 0; 33) 0,25; 34) 2; 35)
.
Примеры для самостоятельного решения:
36)
![]() 37)
37)
![]() 38)
38)
![]() 39)
39)
![]() 40)
40)
![]()
41)
![]() 42)
42)
![]() 43)
43)
![]() 44)
44)
![]() 45)
45)

46)
 47)
47)
![]() 48)
48)
![]() 49)
49)
![]()
50)
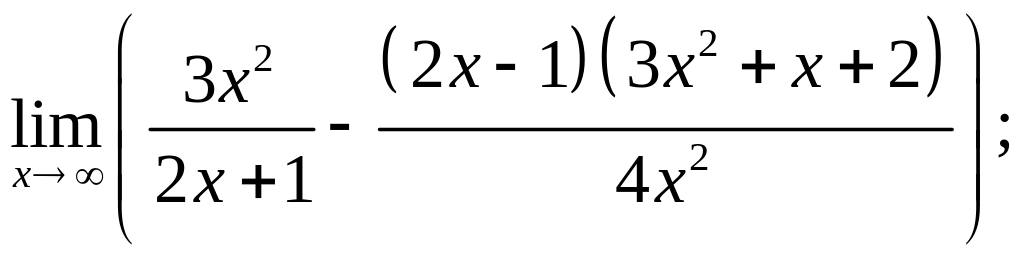 51)
51)
![]() 52)
52)
![]() 53)
53)
![]()
Ответы:
36) 2; 37) 0; 38) 2/3; 39)
6/7; 40) –5/3; 41) 1/6; 42) ½; 43) –2; 44)
![]() 45)
45)
![]() 46) 2/5; 47)
46) 2/5; 47)
![]()
48) ½; 49) –1/2; 50) –1/2; 51) –2,5; 52) 0; 53) 2.
Практическое занятие №4.
Предел функции (продолжение).
Контрольные вопросы.
Первый и второй замечательные пределы.
Что такое бесконечно малое?
Таблица эквивалентных.
Примеры с решениями:
В этих пределах необходимо применять таблицу эквивалентных:
 ;
; ;
; ;
; ;
; ;
; ;
;
При следующем типе неопределенности возможны два способа решения.
Первый способ (применение второго замечательно предела):
 ;
;
Второй способ
(логарифмирование -
![]() ):
):
 ;
; ;
; ;
;
Примеры для практических занятий:
 ;
12)
;
12)
 ;
13)
;
13)
 ;
14)
;
14)
 ;
;
 ;
16)
;
16)
 ;
17)
;
17)
 ;
18)
;
18)
 ;
;
19)
 ;
20)
;
20)
![]() ;
21)
;
21)
![]() ;
22)
;
22)
 ;
;
23)
 ;
24)
;
24)
 ;
25)
;
25)
![]() ;
26)
;
26)
![]() ;
;
27)
![]() ;
28)
;
28)
![]() .
.
Ответы:
11)![]() ;
12)
;
12)
![]() ;
13) 3; 14) 0,25; 15) 3; 16) 18; 17) 2,5; 18) 3; 19) –2; 20)
3; 21)
;
13) 3; 14) 0,25; 15) 3; 16) 18; 17) 2,5; 18) 3; 19) –2; 20)
3; 21)
![]() ;
;
0; 23)
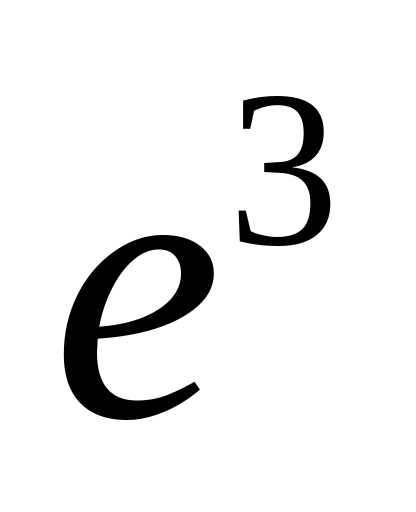 ;
24)
;
25) 1; 26)
;
27) 1; 28)
;
24)
;
25) 1; 26)
;
27) 1; 28)
 .
.
Примеры для самостоятельного решения:
29)
 30)
30)
 31)
31)
 32)
32)
![]()
33)
![]() 34)
34)
![]() 35)
35)
 36)
36)

37)
 38)
38)
 39)
39)
![]() 40)
40)

41)
 42)
42)
 43)
43)
 44)
44)
![]() 45)
45)
![]()
46)
![]() 47)
47)
![]() 48)
48)
![]()
Ответы:
29) 1/2; 30) 5/4; 31) ½; 32)
–1; 33)
;
34) –3/5; 35) -
;
36) 2/3; 37) 1/12; 38)
![]() ; 39)
; 39)
![]() ;
;
40)
![]() ;
41)
;
41)
![]() ;
42)
;
42)
![]() ;
43) 1; 44)
;
43) 1; 44)
![]() ;
45)
;
45)
![]() ;
46)
;
46)
![]() ;
47) 1; 48)
;
47) 1; 48)
![]()
Практическое занятие №5.
Непрерывность функции. Классификация точек разрыва.
Контрольные вопросы.
Какую функцию называют непрерывной?
Какую точку называют точкой устранимого разрыва?
Дайте определение точек разрыва первого и второго рода.
Примеры с решениями:
При каком значении параметра а, функция будет непрерывной:
чтобы функция была непрерывной, необходимо совпадение значений в точке x=1.
![]() или
или
![]() ,
тогда
,
тогда
![]()
![]() - любое число;
- любое число;
теперь два неизвестных параметра у функции, но и две точки 0 и 2 для расчета параметров
![]() или
или
![]() ,
то есть В=0
,
то есть В=0
![]() или
или
![]() ,
т.е. 4А=1, А=1/4;
,
т.е. 4А=1, А=1/4;
Найти точки разрыва и исследовать их характер:
 - функция не
определена в точках
и
- функция не
определена в точках
и .
.
Вычислим односторонние пределы:
![]() -
оба предела бесконечны, следовательно,
в точке 0 разрыв второго рода;
-
оба предела бесконечны, следовательно,
в точке 0 разрыв второго рода;
![]() - оба предела
бесконечны, следовательно, в точке 1
разрыв второго рода.
- оба предела
бесконечны, следовательно, в точке 1
разрыв второго рода.
точка ;
![]() - пределы существуют,
но не равны, следовательно, функция
имеет в точке 0 разрыв первого рода.
- пределы существуют,
но не равны, следовательно, функция
имеет в точке 0 разрыв первого рода.
точка ;
![]() - пределы существуют,
но не равны, следовательно, функция
имеет в точке 0 разрыв первого рода.
- пределы существуют,
но не равны, следовательно, функция
имеет в точке 0 разрыв первого рода.
4.

на
![]() - функция непрерывна, на
- функция непрерывна, на
![]() -
функция разрывна в точке
-
функция разрывна в точке
![]() .
.
![]() - разрыв второго
рода;
- разрыв второго
рода;
 - разрыв второго
рода;
- разрыв второго
рода;
![]() -разрыв
второго рода.
-разрыв
второго рода.
Примеры для практических занятий:
4.

5.
5.

Ответы:
4. а=3; 5. А=В=1.
5. X=3 – разрыв первого рода; 6. X=2 – разрыв первого рода; 7. X=0 – разрыв второго рода ;
8. x=0
– разрыв первого рода; 9.
![]() -
разрыв первого рода.
-
разрыв первого рода.
Примеры для самостоятельного решения:
1) 6.

7.
2)10.
![]()
11.![]()
12.

13.
![]()
Ответы:
6. А=1/2,В=-1; 7. А=1/2,В=0,С=1/4,D=-1/2.
10. X=4 – разрыв первого рода; 11. X=3 – разрыв второго рода; 12. X=0 и x=2 – разрыв первого рода; 13. X=0 – разрыв первого рода.
Практическое занятие №6.
Производные.
Контрольные вопросы:
Сформулируйте определение производной. Укажите ее геометрический смысл.
Что характеризует производная в процессе изменения функции?
Какую функцию называют сложной?
Что такое промежуточный и основной аргументы?
Как находится производная сложной функции?
Примеры с решениями:
Найти производные функции:
 ;
; ;
; ;
; ;
;
Найти производные сложной функции:
 -
это сложная функция, которую можно
представить в виде «цепочки» простых
функций:
-
это сложная функция, которую можно
представить в виде «цепочки» простых
функций:
![]() ,
тогда
,
тогда
![]() ,
,
![]()
 ;
; ;
; ;
; ;
;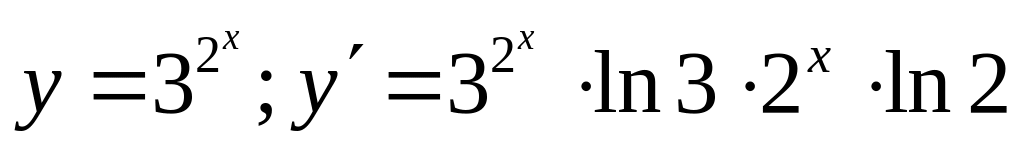 ;
; ;
; ;
;
Примеры для практических занятий:
 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
.
Ответы:
15) ;
16)
;
16)
![]() ;
17)
;
17)
![]() ;
;
18)
![]() ;
19)
;
19)
![]() ;
20)
;
20)
 ;
;
 ;
22)
;
22)
 ;
23)
;
23)
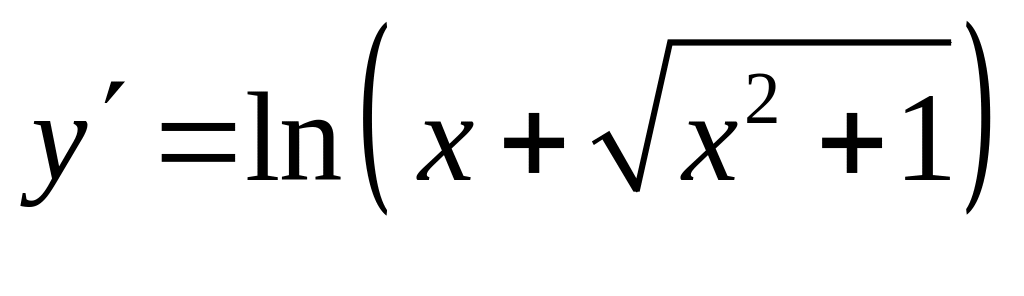 ;
24)
;
24)
 .
.
Примеры для самостоятельного решения:
 26)
26)
 27)
27)

28)
![]() 29)
29)
![]() 30)
30)
![]()
31)
 32)
32)
![]()
Ответы:
25)![]() 26)
26)
![]() 27)
27)
![]() 28)
28)
![]() 29)
29)
![]()
30)
![]() 31)
31)
![]() 32)
32)
![]()
Практическое занятие №7.
Дифференцирование функций.
Контрольные вопросы.
Какой способ задания функции называется параметрическим?
Как найти производную от функции, заданной параметрически?
В чем состоит правило логарифмического дифференцирования?
Дайте определение дифференциала функции и укажите его геометрический смысл.
Дайте определение производных и дифференциалов высших порядков.
Примеры с решениями:
Найти производную
![]() функций, заданных параметрически:
функций, заданных параметрически:
1.

Находим

Тогда
![]()
2.
 при t=1.
при t=1.
Находим

Тогда

3.
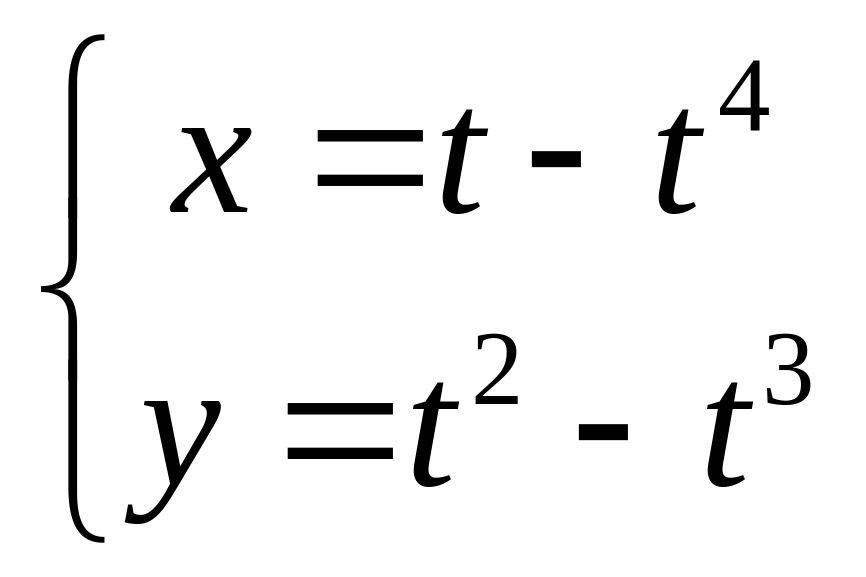 в точке М(0,0).
в точке М(0,0).
Сначала определяем значение t в точке М(0,0):

откуда следует, что производная в этой точке должна иметь два значения (кривая пересекается сама с собой).
Находим
![]()
Для данной точки
имеем
![]()
Продифференцировать данные функции, используя правило логарифмического дифференцирования:
Находим

для нахождения
производной
![]() обозначим
обозначим
![]()
Окончательно

Найти дифференциалы функций:
![]()
7.
![]()

Найти производные и дифференциалы трех первых порядков функции

Находим

Следовательно,
![]()
Примеры для практических занятий:
Найти производную функций, заданных параметрически:
9.

10.
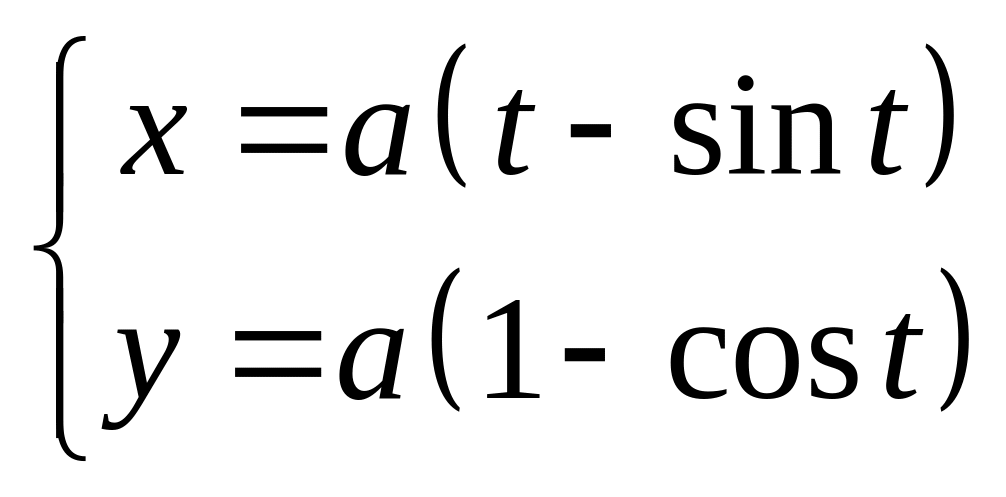 при
при
![]()
11.
![]() в точке
в точке

Продифференцировать функцию, используя правило логарифмического дифференцирования:
12.
![]()
13.

14.
![]()
15.
![]()
Найти дифференциалы функций:
16.
![]()
17.
![]()
Найти дифференциалы третьего порядка функций:
18.
![]()
19.
![]()
Ответы:
 10.
10.
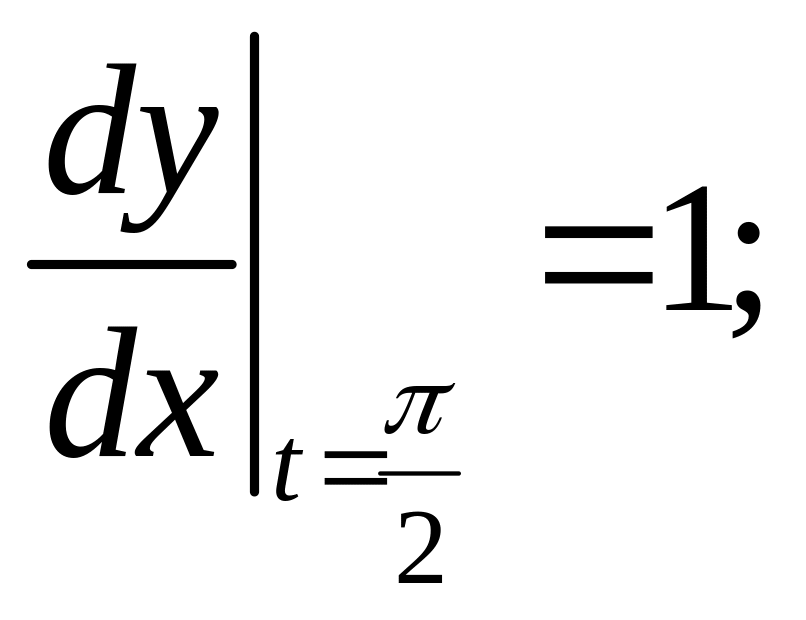 11.
11.
 12.
12.

13.
 14.
14.
![]()
15.
![]()
16.
![]() 17.
17.
![]() 18.
18.
![]() 19.
19.
![]()
Примеры для самостоятельного решения:
Найти производную функций, заданных параметрически:
20.

21.
![]() в точке
в точке

22.

Продифференцировать функции, используя правило логарифмического дифференцирования:
23.
![]()
24.
![]()
25.
![]()
Найти дифференциалы функций:
26.
![]()
27.
![]()
28.
![]()
Найти дифференциалы второго порядка функций:
29.
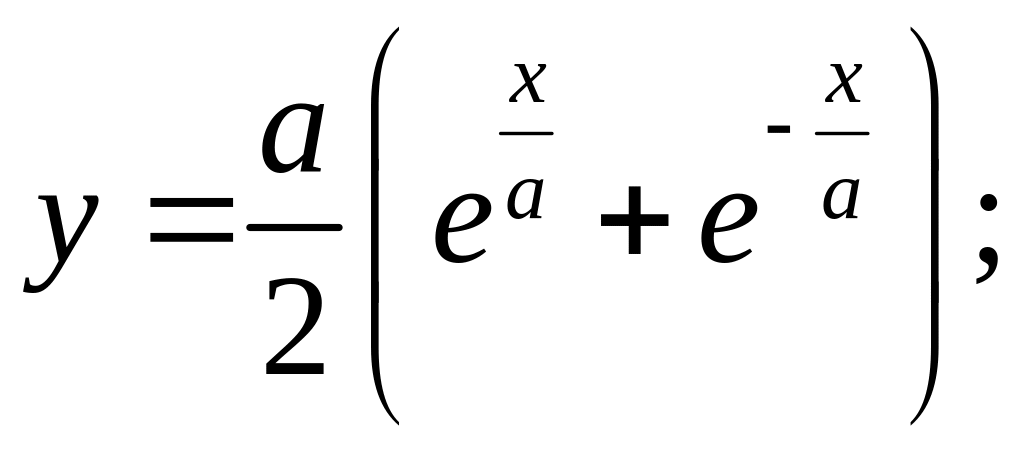
30.
![]()
Ответы:
20.
![]() 21.
21.
![]() 22.
22.
![]()
23.
 24.
24.
![]()
25.
![]() 26.
26.
![]() 27.
27.

28.
![]() 29.
29.
 30.
30.
![]()
Практическое занятие №8.
Правило Лопиталя. Касательная и нормаль к плоской кривой.
Контрольные вопросы.
Сформулируйте правило Лопиталя для раскрытия неопределенности вида

Можно ли применять правило Лопиталя к раскрытию неопределенностей вида
![]() Если можно, то как?
Если можно, то как?
Дайте определение касательной и нормали к плоской кривой и запишите их уравнения.
Примеры с решениями:
Найти указанные пределы по правилу Лопиталя:

Обозначим
![]()

Тогда
![]()
Составить уравнения касательной и нормали к гиперболе
 в точке с абсциссой
в точке с абсциссой

Решение:
Находим

Определяем угловой
коэффициент касательной

Уравнение касательной:
![]()
Уравнение нормали:
![]()
Примеры для практических занятий:
Вычислить указанные пределы по правилу Лопиталя:
 8.
8.
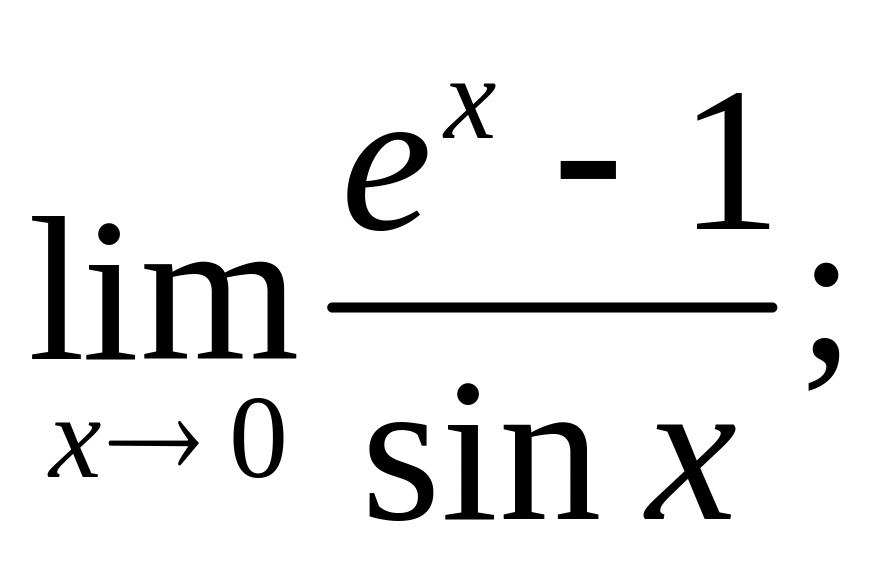 9.
9.
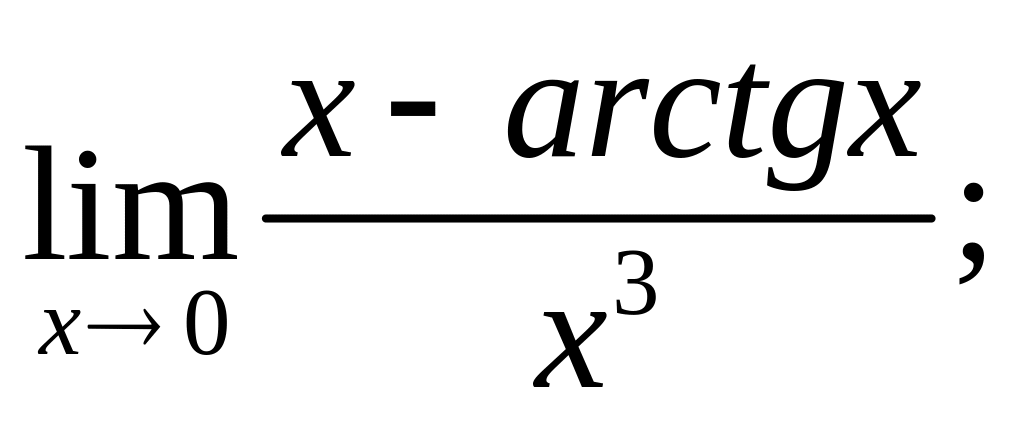 10.
10.
 11.
11.

12.
![]() 13.
13.
![]() 14.
14.
![]() 15.
15.
![]() 16.
16.
![]()
17.
![]() 18.
18.
 19.
19.
![]() 20.
20.
![]() 21.
21.
![]()
22.
![]() 23.
23.
![]() 24.
24.
![]()
Составить уравнения касательной и нормали к кривым в указанных точках.
25.
![]() в точке А(-2,5);
в точке А(-2,5);
26.
![]() в точках пересечения с прямой y=1.
в точках пересечения с прямой y=1.
Ответы:
 8. 1; 9.
8. 1; 9.
 10. –2; 11.
10. –2; 11.
 12. 1; 13.
12. 1; 13.
 14.
14.
 15.
15.
 16. –1; 17. 0; 18. 1;
16. –1; 17. 0; 18. 1;
19. е; 20.
![]() 21. –2; 22.
21. –2; 22.
![]() 23.
23.
![]() 24.
24.
![]() 25.
25.
![]() 26.
26.
![]()
Примеры для самостоятельного решения:
Вычислить указанные пределы по правилу Лопиталя:
27.
![]() 28.
28.
![]() 29.
29.
![]() 30.
30.
![]()
31.
![]() 32.
32.
![]() 33.
33.
![]() 34.
34.
![]()
35.
![]() 36.
36.
![]() 37.
37.
![]() 38.
38.
![]()
39.
![]() 40.
40.
![]()
Написать уравнения
касательной и нормали к графику функций
![]() в заданной точке:
в заданной точке:
41.
![]()
42.
![]()
43. На линии
 найти точку М, в которой касательная
параллельна прямой
найти точку М, в которой касательная
параллельна прямой
![]()
Ответы:
27. 0; 28.
![]() 29.
29.
![]() 30.
31. 1; 32. 1; 33. 0; 34.
30.
31. 1; 32. 1; 33. 0; 34.
![]() 35.
35.
![]() 36.
36.
![]() 37. 1; 38.
37. 1; 38.
![]()
39.
40. 2; 41.
![]() 42.
42.
![]() 43.
43.
![]() при
при
![]()
Практическое занятие №9.
Монотонность и экстремумы функций.
Контрольные вопросы.
1. Сформулируйте необходимое и достаточное условия монотонности функции на промежутке.
2. Дайте определение экстремума функции.
3.Сформулируйте необходимое условие экстремума. Дайте его геометрическую иллюстрацию.
Сформулируйте достаточное условие экстремума функции с помощью первой производной.
Сформулируйте достаточное условие экстремума функции с помощью второй производной.
Критические точки какого типа можно исследовать на экстремум с помощью второй производной?
Как находятся наибольшее и наименьшее значения функции, непрерывной в замкнутом промежутке?
Примеры с решениями:
Найти промежутки монотонности и экстремумы функции

Решение: Эта
функция определена только при
![]()
Находим точки, «подозрительные» на экстремум:

но экстремума в
точках
![]() быть не может, так как они являются
концами области определения, а экстремум
возможен только во внутренних точках
области определения функции.
быть не может, так как они являются
концами области определения, а экстремум
возможен только во внутренних точках
области определения функции.
Находим промежутки монотонности и экстремумы:
X |
-1,1 |
-1 |
0 |
1 |
1,1 |
|
- |
0 |
+ |
0 |
- |
|
|
|
|
|
|
Функция убывает
при
![]()
Функция возрастает
при
![]()
![]()
Замечание 1. Так
как
![]() и
и
![]() являются стационарными, то исследование
на экстремум можно провести с помощью
второй производной.
являются стационарными, то исследование
на экстремум можно провести с помощью
второй производной.
Находим

Замечание 2. Так
как функция непрерывна на замкнутом
промежутке
![]() ,
то можно найти наименьшее и наибольшее
значения функции в этом промежутке. Для
этого вычисляем ее значения в точках,
подозрительных на экстремум
,
то можно найти наименьшее и наибольшее
значения функции в этом промежутке. Для
этого вычисляем ее значения в точках,
подозрительных на экстремум
![]() и
и
![]() ,
а также на концах промежутка
,
а также на концах промежутка
![]() и
и
![]() и находим
и находим
![]()
Примеры для практических занятий:
Найти промежутки монотонности и экстремумы функций:
 3.
3.
 4.
4.
 5.
5.

Найти наибольшее М и наименьшее m значения функций на замкнутом промежутке:
 7.
7.
 8.
8.
 9.
9.

Ответы:
2. возрастает при
![]() убывает при
убывает при
![]()
возрастает при
 убывает при
убывает при
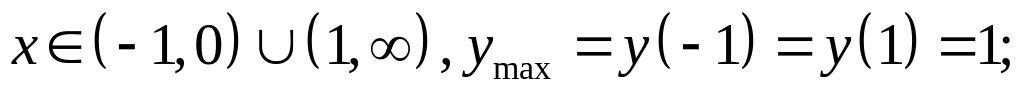
возрастает при
 убывает при
убывает при

возрастает при
 убывает при
убывает при

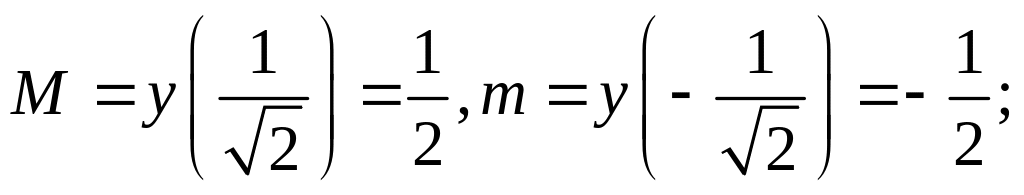



Примеры для самостоятельного решения:
Найти промежутки монотонности и экстремумы функций:
 11.
11.
 12.
12.
 13.
13.
 14.
14.
 15.
15.

Найти наибольшее М и наименьшее m значения функции на замкнутом промежутке:
16.
![]()
17.
![]()
18.
![]()
Ответы:
10.убывает при![]() возрастает при
возрастает при
![]()
убывает при возрастает при

убывает при
 возрастает при
возрастает при

убывает при
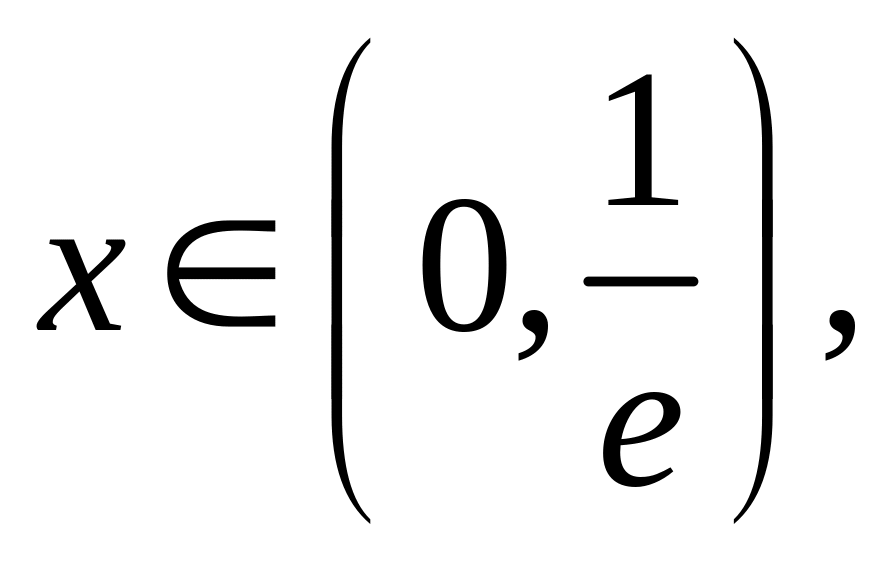 возрастает при
возрастает при

убывает при
 возрастает при
возрастает при
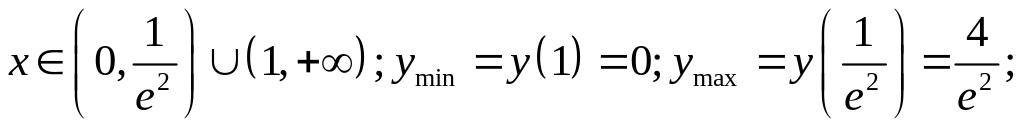
убывает при
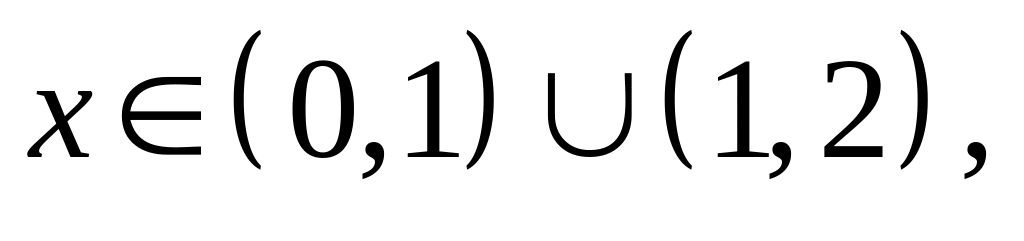 возрастает при
возрастает при




Практическое занятие №10.
Выпуклость и вогнутость кривой. Точки перегиба. Асимптоты кривой. Построение кривой по ее уравнению в явном виде.
Контрольные вопросы.
Что такое «выпуклость» и «вогнутость» кривой?
Что такое точка перегиба кривой?
Что является необходимым, а что достаточным условием существования перегиба в данной точке?
Дайте определение вертикальной и наклонной асимптоты кривой.
Как определяются параметры наклонной асимптоты кривой?
Изложите общую схему исследования функции

Примеры с решениями:
Определить точки перегиба и характер вогнутости кривой

Решение:
![]()
Находим

![]() - критические точки
на перегиб.
- критические точки
на перегиб.
![]()
x |
-2 |
|
-1 |
0 |
1 |
|
2 |
|
- |
0 |
+ |
0 |
- |
0 |
+ |
|
|
|
|
0 |
|
|
|
|
|
Точка Перегиба |
|
точка перегиба |
|
точка перегиба |
|
Ответ:
 - точки перегиба;
- точки перегиба;
при
![]() - вогнутость вниз,
- вогнутость вниз,
при
![]() - вогнутость вверх.
- вогнутость вверх.
Определить асимптоты кривой

Решение:
![]() -
вертикальная асимптота, так как
-
вертикальная асимптота, так как
![]()
Находим наклонную асимптоту:
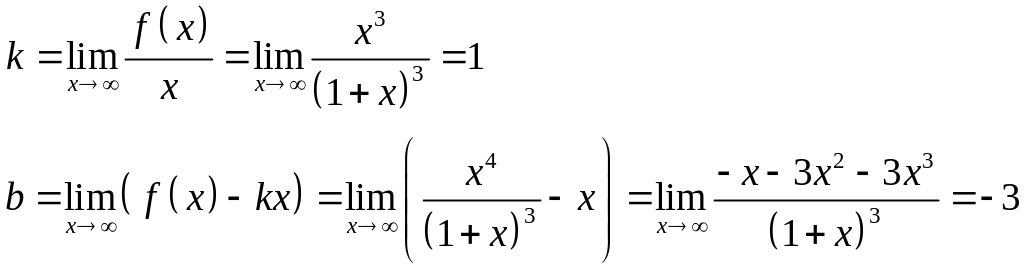
![]() - наклонная
асимптота.
- наклонная
асимптота.
Провести полное исследование функции
 и построить эскиз графика.
и построить эскиз графика.
Решение:

![]() - критические точки
на экстремум.
- критические точки
на экстремум.
![]()
x |
-4 |
-3 |
-2 |
-1 |
-1/2 |
0 |
1 |
|
+ |
0 |
- |
точка |
+ |
0 |
+ |
|
|
|
|
разрыва |
|
Экстремума нет |
|
![]() - критическая точка
на перегиб
- критическая точка
на перегиб
![]()
X |
-1/2 |
0 |
1 |
|
- |
0 |
+ |
Y |
|
0 |
|
О(0,0) – точка перегиба.
Определяем асимптоты кривой:

![]() - наклонная
асимптота.
- наклонная
асимптота.
- вертикальная
асимптота, так как
![]() .
.
Строим эскиз графика кривой:
 y
y




-1 2 x
-1


Примеры для практических занятий:
Определить точки перегиба и характер вогнутости (выпуклости) кривых:
 5.
5.
 6.
6.

Определить асимптоты кривых:
 8.
8.
 9.
9.

Провести полное исследование и построить эскизы графиков функций:
 11.
11.
 12.
12.

Ответы:
4.![]() - кривая выпукла,
- кривая выпукла,
![]() -
кривая вогнута, точек перегиба нет;
-
кривая вогнута, точек перегиба нет;
 - промежутки
вогнутости,
- промежутки
вогнутости,
![]() - промежутки
выпуклости,
- промежутки
выпуклости,
![]() - точки перегиба;
- точки перегиба;
 - промежуток
выпуклости,
- промежуток
выпуклости,
 - промежуток вогнутости,
- промежуток вогнутости,
 - точка перегиба;
- точка перегиба;

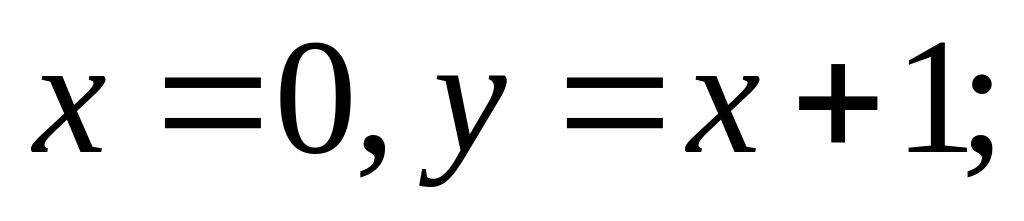
 - точка перегиба;
- точка перегиба;
 - асимптоты;
- асимптоты; - точка перегиба;
- точка перегиба;
 - асимптоты;
- асимптоты; - точка перегиба;
- точка перегиба;
 - асимптоты.
- асимптоты.
Примеры для самостоятельного решения:
Провести полное исследование функций и построить эскизы графиков:
 14.
14.
 15.
15.
 16.
16.

Ответы:
 - точки перегиба,
- точки перегиба,
![]() - асимптота.
- асимптота.
14.
![]() - абсциссы точек перегиба,
- абсциссы точек перегиба,
![]() - асимптоты.
- асимптоты.
15.
![]() - точка перегиба,
- точка перегиба,
![]() - асимптоты.
- асимптоты.
16.
![]() - абсцисса точки перегиба,
- абсцисса точки перегиба,
![]() -
асимптоты.
-
асимптоты.
Практическое занятие №11.
Непосредственное интегрирование.
Контрольные вопросы.
В чем состоит задача интегрального исчисления?
Какая функция называется первообразной для данной функции f(x)? Указать ее основные свойства?
Дайте определение неопределенного интеграла для данной функции f(x).
Перечислите основные свойства неопределенного интеграла.
В чем состоит метод непосредственного интегрирования?
В чем состоит обобщение таблицы интегралов?
Укажите основные преобразования дифференциала (подведение под знак дифференциала).
Примеры с решениями:
Найти интегралы:
1)![]() =
=
 ;
;
2)![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
 ;
;
6)

7) ![]() ;
;
8) ![]() ;
;
9) ![]() ;
;
10) ![]() .
.
Примеры для практических занятий:
Найти интегралы:
11) ![]() ;
12)
;
12)![]() ;
13)
;
13) ![]() ;
14)
;
14) ![]() ;
15)
;
15) ![]() ;
;
16) ![]() ;
17)
;
17)
![]() ; 18)
; 18) ![]() ;
19)
;
19) ![]() ;
;
20) ![]() ;
21)
;
21) ![]() ;
22)
;
22) ![]() ;
23)
;
23) ![]() ;
24)
;
24) ![]() ;
25)
;
25) ![]() .
.
Ответы:
11)![]() ; 12)
; 12)![]() ; 13) 2
; 13) 2![]() ;
14)
;
14) ![]() ;15)
ln(
;15)
ln(![]() ;
;
16)![]() ;
17) ln
;
17) ln![]() ;
18)
;
18) ![]() ;
19)
;
19) ![]() ;
;
20) -2![]() ;
21) arcsin
;
21) arcsin![]() ;
22) -
;
22) -![]() +
+![]() ;
23)
;
23) ![]() ;
;
24) -![]() ;
25)
;
25) ![]() .
.
Примеры для самостоятельного решения:
Найти интегралы:
26)![]() ;
27)
;
27)![]() ;
28)
;
28)![]() ;
29)
;
29)![]() ;
30)
;
30)![]() ;
31)
;
31)![]() ;
;
32)![]() ;
33)
;
33)![]() ;
34)
;
34)![]() ;
35)
;
35)![]() ;
36)
;
36)![]() dx;
37)
dx;
37)![]() ;
;
38)![]() ;
39)
;
39)![]() ;
40)
;
40)![]() .
.
Ответы:
26) ![]() ;
27) -
;
27) -![]() ;
28)
;
28) ![]() ;
29) -
;
29) - ![]() ;
30) -2
;
30) -2![]() ;
;
31) -![]() ;
32)
;
32) ![]() ;
33) -
;
33) -![]() ;
34) 3
;
34) 3![]() ;
35)
;
35) ![]() ;
;
36)
![]() ;
37) -
;
37) -![]() ;
38)
;
38)![]() ;
39)
;
39)![]() ;
40)
;
40)![]() .
.
Практическое занятие №12.
Метод замены переменной (подстановки).
Контрольные вопросы:
1. В чем состоит смысл интегрирования подстановкой?
Каким условиям должна удовлетворять функция
 ,
используемая в качестве подстановки?
,
используемая в качестве подстановки?Указать наиболее употребительные подстановки.
Примеры с решениями:
1.
![]() =
= ![]() =
=
=
=![]() =
=![]() +
+![]() +c
=
+c
= ![]() +
+ ![]() + c;
+ c;
2.

3.
dx = ![]() =
= ![]() = 2
= 2![]() + c = 2
+ c = 2![]() + c;
+ c;
 dx
=
dx
=  =
=

![]()
5.

![]()
![]() + с.
+ с.
Примеры для практических занятий:
Используя подходящую подстановку, найти следующие интегралы:
6. ![]() ;
7.
;
7. ![]() ;
8.
;
8.![]() ;
9.
;
9.
![]() ; 10.
; 10.![]() ;
;
11.![]() ;
12.
;
12.![]() ;
13.
;
13.![]() ;
14.
;
14.![]() ;
15.
;
15.![]() ;
;
16.![]() ;
17.
;
17.![]() ;
18.
;
18.![]() ;
19.
;
19.![]() ;
20.
;
20.![]() .
.
Ответы:
6. – ![]() (x =
(x = ![]() );
7. 2arctg
);
7. 2arctg![]() (
(![]() ;
;
8.
![]() (t =
(t = ![]() ;
9.
;
9. ![]() (t = lnx);
(t = lnx);
10. 2ln(![]() (t
=
;
(t
=
;
11. ![]() ;
;
12. ![]() );
);
13.![]() ;
;
14. 2![]() ;
;
15. ![]() ;
;
16.
![]() 17.
17. ![]() +c
(x=2tgt);
+c
(x=2tgt);
18.![]() ;
;
19. 2![]() ;
;
20.![]() .
.
Примеры для самостоятельного решения:
Найти интегралы:
21.![]() ;
22.
;
22.![]() ;
23.
;
23.![]() ;
24.
;
24.![]() ;
;
25.![]() ;
26.
;
26. ![]() ;
27.
;
27. ![]() ;
28.
;
28. ![]() ;
29.
;
29. ![]() ;
;
30.
![]() ; 31.
; 31. ![]() ;
32.
;
32. ![]() ;
33.
;
33. ![]() ;
;
34. ![]() ;
35.
;
35. ![]() .
.
Ответы:
21.
 ; 22.
; 22. ![]() ;
;
23. ln(![]() ;
24.
;
24. ![]() +c;
25.
+c;
25. ![]() )+c;
)+c;
26. ![]() ;
27.
;
27. ![]() +c;
+c;
28. 2arcsin![]() ;
29.
;
29. ![]() ;
30.
;
30.

31.
![]() 32.
32.
![]() ;
;
33.
![]() 34.
34.![]() + c; 35.
+ c; 35. ![]() .
.
Практическое занятие №13.
Интегрирование по частям.
Контрольные вопросы.
1. Записать и прочесть формулу интегрирования по частям.
2. Когда целесообразно применять формулу интегрирования по частям?
3. Указать план интегрирования по указанной формуле.
4. Перечислить основные типы интегралов, вычисляемых с помощью формулы интегрирования по частям.
5. Указать, что обозначается за U и dV в указанных выше типах интегралов.
Примеры с решениями:
Найти интегралы:
1)
![]()
2)
=
 ;
;
4)

Примеры для практических занятий:
Найти интегралы:
5) ![]() 6)
6)
![]() 7)
7)
![]() 8)
8)
![]()
9)
![]() 10)
10)
![]() 11)
11)![]() ;
12)
;
12) ![]()
13)
![]() ;
14)
;
14)![]() ;
15)
;
15)![]() ;
16)
;
16)
![]()
Ответы:
5)
![]() 6)
6)![]()
7)
![]() 8)
8)
![]()
9)
![]() 10)
10)
![]()
11)
![]() 12)
12)
![]()
13)
![]() 14)
14)
![]()
15)![]() 16)
16)
![]()
















 Y
Y




 y
y


 y
y