Задание 92
Найти указанные пределы, не пользуясь правилом Лопиталя.
127. а)
;
б)
;
в)
;
г)
.
Решение
а) Подстановка предельного значения
аргумента приводит к неопределенности
.
Разделим числитель и знаменатель на
старшую степень аргумента, т.е. наx4.
Получим
,
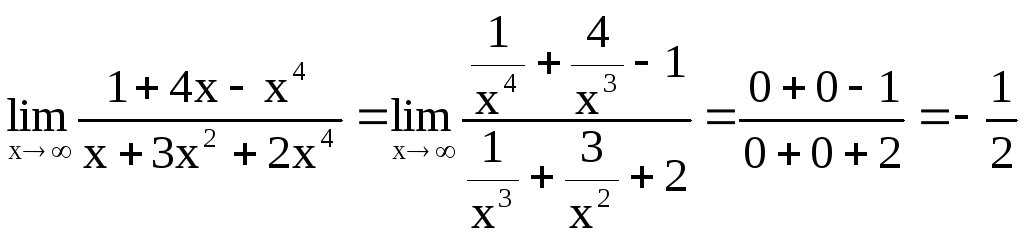так как при
,
,
,
и
–
бесконечно малые функции.
б) Непосредственная
подстановка аргумента х = – 4 приводит
к неопределенности вида
.
Избавимся от иррациональности в
числителе, домножив числитель и
знаменатель на
,
а знаменатель разложим на множители:
х2+ 2х – 8 = 0;
D = 4 + 32 = 36;
x1= (–2 – 6) / 2 = –4, x2= (–2 + 6) / 2 = 2.
х2+ 2х – 8 = (x + 4)(x – 2)
(
)(
)
= х + 12 – 4+х = 2 х + 8=2 (x+4).
Тогда:
=
.
в) Непосредственная
подстановка аргумента х = –1 приводит
к неопределенности вида
.
Заменяя 1 –cos3x– 1 = 2sin2
,
получим:
=
= 4,5
Здесь использован
первый замечательный предел
г) При х → +имеем неопределенность вида· (–), которую преобразуем, используя свойство логарифмической функции:
(2х + 3) · [ln(x+ 2) –lnx] =
(2х + 3) ·ln
=ln
=ln
.
Тогда
=
[имеем неопределенность вида 1,
раскроем ее с помощью 2-го замечательного
предела
]=
=
=
4.
Задание 102
Заданы функция у = f(x)
=
и два значения аргумента х1= 2 и
х2= 4. Требуется: 1) установить,
является ли данная функция непрерывной
или разрывной для каждого из данных
значений аргумента; 2) в случае разрыва
функции найти ее пределы при приближении
к точке разрыва слева и справа; 3) сделать
схематический чертеж.
Решение
1) Так f(x) является элементарной функцией, то она непрерывна во всех точках, в которых определена. Следовательно, в точке х1= 2 функция непрерывна, а в точке х2= 4 она не является непрерывной (деление на ноль неопределенно). Значит, х2= 4 – точка разрыва функции.
2) Вычислим односторонние пределы в точке х2= 4:
Один из пределов оказался бесконечным, поэтому х2= 4 – точка разрыва 2-го рода.
3) Учитывая, что
,
строим схематический график функции.
y= 1
Задание 112
Задана функция y=f(x) =
различными аналитическими выражениями
для различных областей изменения
независимой переменной. Найти точки
разрыва функции, если они существуют.
Сделать чертеж.
Решение
Функция x–3 непрерывна
на (–; 0), функцияx+1 непрерывна на [0; 4], а
– непрерывна на (4; +),
значитf(x)
непрерывна на интервалах (–;
0)
[0;
4]
(4;
+).
Исследуем поведение функции в точках х1= 0 и х2= 4. Находим правые и левые пределы функции в этих точках.
;f(0) = 1.
Так как односторонние пределы конечны, но не равны между собой, то функция терпит разрыв 1-го рода, т. е. х1= 0 – точка разрыва 1-го рода.
Рассмотрим точку х2= 4:
f(4) = 5.
Так как односторонние пределы функции в точке х2= 4 равны между собой и равны значению функции в этой точке, то функцияf(x) в точкеx2= 4 непрерывна.
Сделаем чертеж:
