Задание 62

Привести к каноническому виду уравнение линии второго порядка, используя теорию квадратичных форм.

4х²+ 2ху + 3у²= 24.

Решение

Левая часть уравнения 4х²+ 2ху + 3у²= 24 представляет собой квадратичную форму с матрицей.

Решаем характеристическое уравнение

т.е..

(4 – λ)(3 – λ) – 6 = 0;

12 – 7λ + λ²– 6 = 0;

λ²– 7λ + 6 = 0;

D= 49 – 24 = 25;

λ₁= (7 – 5) / 2 = 1, λ₂= (7 + 5) / 2 = 6.

λ₁= 1, λ₂= 6 – характеристические числа.

Находим собственные векторы из системы уравнений .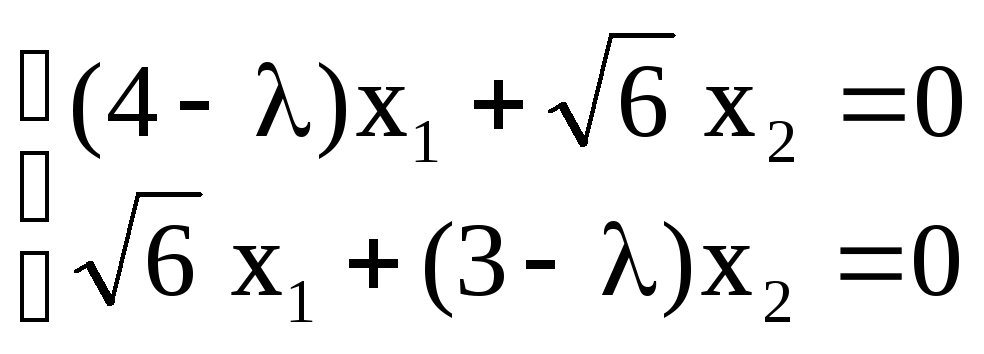

Полагая λ = λ₁= 1, получаем систему уравнений для первого вектора: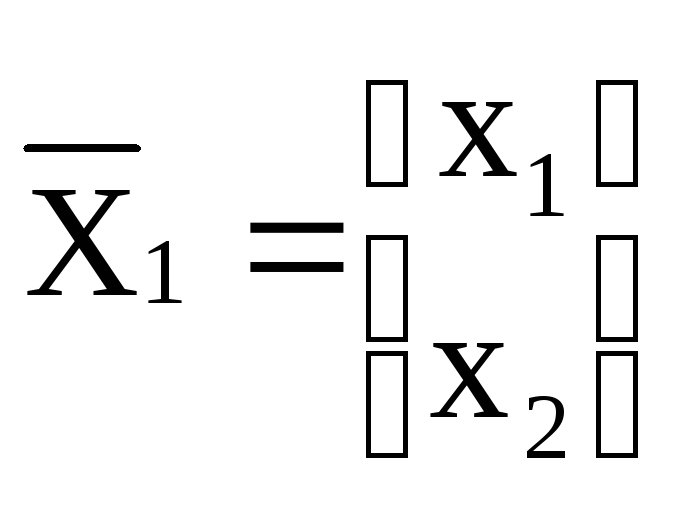

х₁= –х₂.

Пусть х₂=, тогда х₁= –и– собственный вектор, соответствующий λ₁=1.

Полагая λ = λ₂= 6, получаем систему уравнений для второго вектора:

х₂=х₁.

Пусть х₁=, тогда х₂=и– собственный вектор, соответствующий λ₂= 6.

Нормируем собственные векторы , получаем,. Составляем матрицу перехода от старого базиса к новому, в которой координаты нормированных собственных векторов записаны по столбцам. Выполняя преобразование

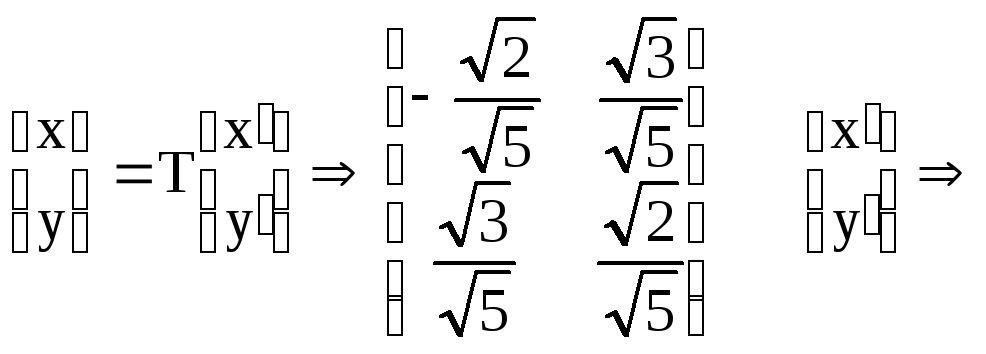
или

Найденные для х и у выражения подставим в исходное уравнение кривой:

4 · (–х′ +у′)²+ 2·(–х′ +у′)(х′ +у′) + 3 ·(х′ +у′)²– 24 = 0;

2х′²– 2х′у′ + 3у′² ) +–х′²–2 х′у′ +3 х′у′ +у′²)+(3х′²+х′у′+ + 2у′²)– 24 = 0;

х′² –х′у′ +у′² –х′²+х′у′ +у′²+х′²+х′у′ +у′²–24 = 0;

х′²+ 6у′²– 24 = 0;

– каноническое уравнение эллипса.

Задание 72

Построить график функции у = –3sin(2x+ 3) преобразованием графика функцииy=sin x.

Решение

Строим график функции y=sin x, затем строим график функцииy=sin 2xсжатиемy=sin xв 2 раза к оси Оу. Графикy=sin(2x+ 3) =sin2(x+ ) получается параллельным переносом графикаy=sin2xв отрицательном направлении оси Ох на. Растяжением в 3 раза вдоль оси Оу и отображением относительно оси Ох графикаy=sin(2x+ 3) получаем график функции у = – 3sin(2x+ 3).

Изобразим соответствующие графики:

Задание 82

Дана функция r=на отрезке 0φ2π. Требуется: 1) построить график функции в полярной системе координат по точкам, даваязначения через промежуток/8, начиная от=0; 2) найти уравнение полученной линии в прямоугольной декартовой системе координат, начало которой совпадает с полюсом, а положительная полуось абсцисс – с полярной осью, и по уравнению определить, какая это будет линия.

Решение

1) Составим таблицу:

	φ	cos φ	r=
1	0	1	1,2
2	π/8	0.924	1,24
3	π /4	0,707	1,36
4	3π/8	0,383	1,59
5	π/2	0	2
6	5π/8	-0.383	2,69
7	3π/4	-0,707	3,78
8	7π/8	-0,924	5,21
9	π	-1	6
10	9π/8	-0,924	5,21
11	5π/4	-0,707	3,78
12	11π/8	-0,383	2,69
13	3π/2	0	2
14	13π/8	0,383	1,59
15	7π/4	0,707	1,36
16	15π/8	0,924	1,24
17	2π	1	1,2

Проведем из начала координат лучи под углами 0, к полярной оси и отложим на них соответствующие значенияr. Соединим эти точки плавной линией и получим изображение кривой.

Сделаем чертеж:

Найдем уравнение этой кривой в декартовых координатах. Для этого подставим в исходное уравнение r=,cosφ=.

Получим: =.

Преобразуем это соотношение: =;

3+ 2x= 6;= 6 – 2x.

Возведем обе части равенства в квадрат:

9(х²+ у²) = (6 – 2x)²; 9х²+9у²= 36 – 24x+ 4x²;

5х²+24x+9у² –36=0.

Выделим полный квадрат по переменной x:

5(х²+)+9у² –36=0;

5(х²+9у² –36=0;

5(x+)²– +9у² –36=0;

5(x+)²+9у² =;

Разделим обе части на :

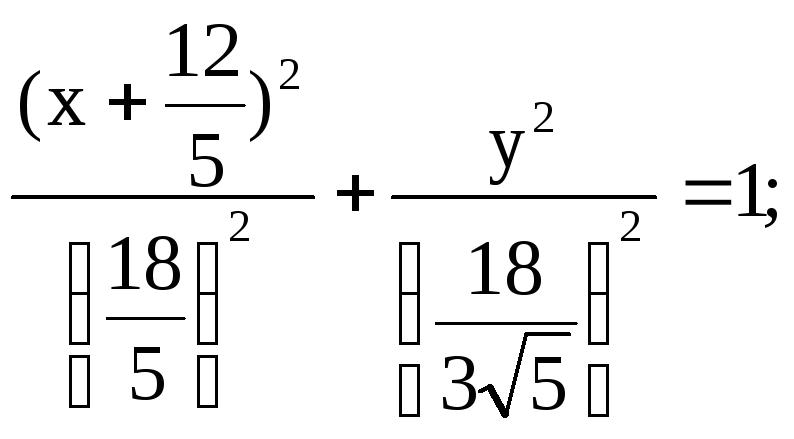
Получим уравнение эллипса с полуосями a=b=, центр которого сдвинут влево по оси Ох на.