
- •Вычисление двойного интеграла.
- •Замена переменных в двойном интеграле.
- •Геометрические приложения двойных интегралов.
- •Тройной интеграл.
- •Замена переменных в тройном интеграле.
- •Приложения тройного интеграла.
- •Криволинейные интегралы I рода.
- •Криволинейный интеграл II рода.
- •Формула Грина.
- •Нахождение функции по её полному дифференциалу.
Криволинейный интеграл II рода.
Криволинейный
интеграл по координатам (или криволинейный
интеграл II
рода) от выражения
![]() по дуге кривой L
имеет вид:
по дуге кривой L
имеет вид:
![]() .
.
Пример 8.
Вычислить
криволинейный интеграл
![]() ,
где L
– дуга параболы
,
где L
– дуга параболы
![]() от точки
от точки
![]() до точки
до точки
![]() .
.

Формула Грина.
Если D
– некоторая замкнутая область на
плоскости
,
ограниченная контуром L,
и на ней заданы функции
![]() и
и
![]() ,
непрерывные на D
вместе со своими частными производными
,
непрерывные на D
вместе со своими частными производными
![]() и
и
![]() ,
то имеет место формула Грина
,
то имеет место формула Грина
![]() .
.
Пример 9.
Вычислить с помощью
формулы Грина криволинейный интеграл
![]() ,
где
,
где
![]() - окружность
- окружность
![]() .
.
![]() ,
,
![]()
![]() ,
,
![]() .
.
Следовательно,
![]() ,
где D
– круг
.
Перейдём к полярным координатам
,
где D
– круг
.
Перейдём к полярным координатам
![]() ,
,
![]() ,
,
![]() ,
уравнение окружности:
,
уравнение окружности:
![]()
![]()
Нахождение функции по её полному дифференциалу.
Область G на плоскости называется односвязной, если для любого замкнутого контура, лежащего в этой области, ограниченная им часть плоскости целиком принадлежит области G.
Для того, чтобы
криволинейный интеграл
![]() не зависел от линии интегрирования
не зависел от линии интегрирования
![]() ,
необходимо и достаточно, чтобы во всех
точках односвязной области D
соблюдалось равенство
,
необходимо и достаточно, чтобы во всех
точках односвязной области D
соблюдалось равенство
![]() . (11)
. (11)
Выполнение условия
(11) в области D
приводит к следующему условию: выражение
является полным дифференциалом некоторой
функции
![]() ,
,
![]() .
Функция
.
Функция
![]() может быть найдена по формуле
может быть найдена по формуле
 , (12)
, (12)
где
![]() - любая фиксированная точка области D,
- любая фиксированная точка области D,
![]() - переменная точка.
- переменная точка.
Пример 10.
Найти функцию ,
если
![]() .
.
Нетрудно убедиться,
что условие (11) выполняется. Действительно,
![]()
![]()
![]()
![]()
Для вычисления функции воспользуемся формулой (12):

Таким образом,
![]()
Индивидуальные задания
Изменить порядок интегрирования:
1.1 |
|
1.2 |
|
1.3 |
|
1.4 |
|
1.5 |
|
1.6 |
|
1.7 |
|
1.8 |
|
1.9 |
|
1.10 |
|
1.11 |
|
1.12 |
|
1.13 |
|
1.14 |
|
1.15 |
|
1.16 |
|
1.17 |
|
1.18 |
|
1.19 |
|
1.20 |
|
1.21 |
|
1.22 |
|
1.23 |
|
1.24 |
|
1.25 |
|
1.26 |
|
1.27 |
|
1.28 |
|
1.29 |
|
1.30 |
|
Вычислить двойной интеграл по области D, ограниченной заданными линиями:
Перейдя к полярной системе координат, вычислить двойной интеграл:

 - первый лепесток кривой
- первый лепесток кривой
 ;
;

 - один лепесток кривой
- один лепесток кривой
 ;
;
















































Вычислить площади плоских фигур, ограниченных данными линиями:
 ,
,
 ,
,
 ,
,
 ;
; ,
,
 ;
; ,
,
 ;
;первый лепесток кривой
 ;
; ,
,
 ;
; ,
,
 ,
,
,
,
 ;
; ,
,
 ;
; ,
,
 ;
; ,
,
 ;
; ;
; ,
,
 ;
; ,
,
 ;
; ,
,
 ;
; ,
,
 ,
,
,
,
 ;
; ,
,
 ;
; ,
,
 ;
;, , ,
 ;
; ,
,
,
,
 ;
; ,
,
 ,
,
 ;
; ,
,
 ;
; ,
,
 ,
,
 ;
; ,
,
 ,
,
,
,
 ;
; ,
,
 ;
; ,
,
 ;
; ,
,
,
;
,
,
,
; ,
,
 ;
; ,
,
 ;
; ,
,
 ;
; ,
,
 ,
вне параболы;
,
вне параболы; ,
,
 ,
,
 .
.
Вычислить тройной интеграл по области
 ,
ограниченной указанными поверхностями:
,
ограниченной указанными поверхностями:
 ,
,  ;
; ,
,  ;
; ,
,  ;
; ,
,  ;
; ,
,  ;
; ,
,  ;
; ,
,  ;
; ,
,  ;
;,
 ;
;
 ,
,  ;
; ,
,  ;
; ,
,  ;
; ,
,  ;
; ,
;
,
; ,
,  ;
; ,
,  ;
; ,
,  ;
; ,
,  ;
;,
 ;
; ,
,  ;
;,
 ;
; ,
,  ;
; ,
,  ;
;,
 ;
;,
 ;
; ,
,  ;
; ,
,  ;
; ,
,  ;
; ,
;
,
; ,
, 
Вычислить объём тела, ограниченного поверхностями:
 ,
,
 ,
,
 ;
; ,
,
 ,
,
 ,
,
 ,
,
 ;
; ,
,
 ,
;
,
; ,
,
,
,
 ;
; ,
,
 ,
;
,
; ,
,
 ,
,
 ,
;
,
; ,
,
,
,
,
,
 ,
,
 ;
; ,
,
 ,
,
 ;
; ,
,
 ,
;
,
; ,
,
 ,
;
,
;, , ,
 ;
; ,
,
,
,
 ,
;
,
; ,
,
,
,
;
,
,
,
,
; ,
,
 ,
;
,
;,
 ,
,
;
,
,
; ,
,
 ,
;
,
;, , ,
 ,
,
 ;
; ,
,
 ,
,
;
,
,
; ,
,
,
,
 ;
; ,
,
 ;
; ,
,
 ,
,
;
,
,
;,
 ,
,
,
,
 ;
; ,
,
,
,
;
,
,
,
,
; ,
,
;
,
,
;, , ;
 ,
,
 ,
,
 ,
;
,
; ,
,
 ,
,
,
;
,
,
,
; ,
,
 ,
,
,
;
,
,
,
;, ,
 ;
;, , , , .
Вычислить криволинейный интеграл первого рода:
 ,
- контур треугольника с вершинами
,
- контур треугольника с вершинами
 ,
,
 ,
,
 ;
; ,
, 
 ,
, 
 ,
, 
 ,
- замкнутый контур, ограниченный линиями
,
,
,
,
- замкнутый контур, ограниченный линиями
,
,
,
 ;
; ,
- отрезок прямой от точки
до
,
- отрезок прямой от точки
до
 ;
; ,
, 
, - дуга линии от точки
 до
до
 ;
;, - отрезок прямой от точки
 до
до
 ;
; ,
- дуга
,
- дуга
 ,
,
;
,
,
; ,
- отрезок прямой от точки
,
- отрезок прямой от точки
 до
до
 ;
;,
 ;
; ,
- контур параллелограмма с вершинами
,
- контур параллелограмма с вершинами
 ,
,
 ,
,
 ,
,
 ;
; ,
- отрезок прямой от точки
,
- отрезок прямой от точки
 до
до
 ;
; ,
- первый виток винтовой линии
,
- первый виток винтовой линии
 ,
,
 ,
,
 ;
; ,
- отрезок прямой от точки
,
- отрезок прямой от точки
 до
до
 ;
; ,
- отрезок прямой от точки
,
- отрезок прямой от точки
 до
до
 ;
; ,
, 
 ,
- контур треугольника с вершинами
,
- контур треугольника с вершинами
 ,
,
 ,
,
 ;
;, - отрезок прямой
 от
точки
от
точки
 до
до
 ;
; ,
- отрезок прямой от точки
,
- отрезок прямой от точки
 до
до
 ;
; ,
, 
 ,
- отрезок прямой от точки
,
- отрезок прямой от точки
 до
до
 ;
; ,
- дуга линии
,
- дуга линии
 от точки
до точки
от точки
до точки
 ;
; ,
- контур треугольника с вершинами
,
- контур треугольника с вершинами
 ,
,
 ,
,
 ;
; ,
, 
 ,
, 
 ,
- контур треугольника с вершинами
,
- контур треугольника с вершинами
 ,
,
 ,
,
 ;
;, - контур треугольника с вершинами
 ,
,
 ,
,
 ;
; ,
- коническая винтовая линия
,
- коническая винтовая линия

Вычислить криволинейный интеграл второго рода:
 ,
, 
 ,
,
 ;
;
 ;
;




 - контур треугольника с вершинами
,
- контур треугольника с вершинами
,
 ,
,
 ;
; ,
- ломаная ОАВ, где
,
,
- ломаная ОАВ, где
,
 ,
,
 ;
; ,
- отрезок прямой от точки
,
- отрезок прямой от точки
 до
до
 ;
; ,
,
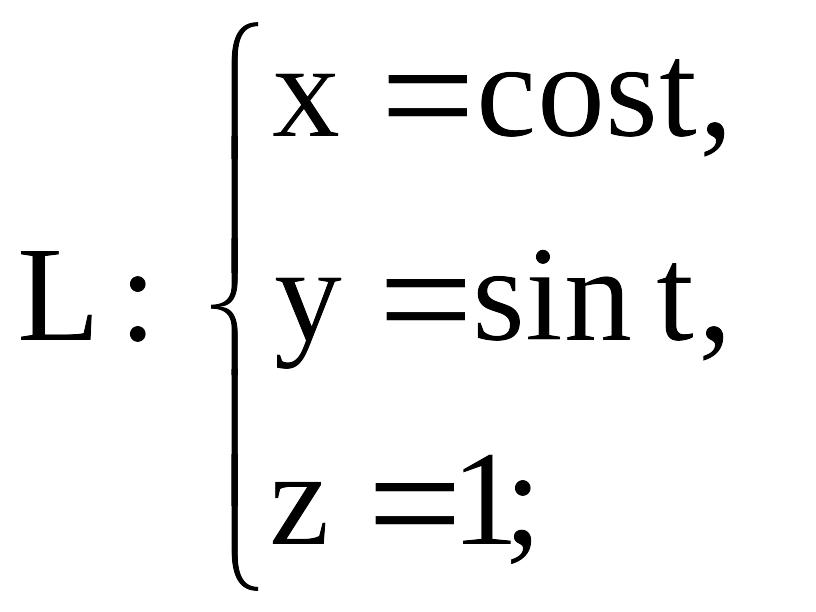


 - контур треугольника с вершинами
,
,
- контур треугольника с вершинами
,
,
 ;
; - ломаная ОАВ, где
,
- ломаная ОАВ, где
,
 ,
,
 ;
;

 - дуга линии
- дуга линии
 от точки
до точки
от точки
до точки
 ;
; - дуга линии
- дуга линии
 от точки
от точки
 до точки
до точки
 ;
;
 - отрезок прямой
- отрезок прямой
 от точки
до
;
от точки
до
;

 - дуга линии
- дуга линии
 от точки
от точки
 до точки
до точки
 ;
;






 - контур треугольника с вершинами
- контур треугольника с вершинами
 ,
,
 ,
,
 ;
;

- контур треугольника с вершинами
 ,
,
 ,
,
 ;
;

- дуга линии от точки до ;
 - дуга линии
- дуга линии
 от точки
до
.
от точки
до
.
Вычислить криволинейный интеграл с помощью формулы Грина:
 - контур, образованный линиями
- контур, образованный линиями
 ,
;
,
; - контур, образованный линиями
,
,
- контур, образованный линиями
,
,
 ;
;
 ;
; - контур треугольника с вершинами
,
,
;
- контур треугольника с вершинами
,
,
; ;
; - контур, образованный линиями
,
- контур, образованный линиями
,
 ,
;
,
;- контур, образованный линиями , ;
 - контур, образованный линиями
,
,
;
- контур, образованный линиями
,
,
; - контур треугольника с вершинами
,
- контур треугольника с вершинами
,
 ,
,
 ;
; ;
; - контур, образованный линиями
- контур, образованный линиями
 ,
,
;
,
,
; - контур треугольника с вершинами
,
,
- контур треугольника с вершинами
,
,
 ;
; - контур, ограничивающий область
- контур, ограничивающий область
 ,
,
 ;
;

 - контур треугольника с вершинами
,
- контур треугольника с вершинами
,
 ,
,
 ;
;

 - контур, образованный линиями
- контур, образованный линиями
 ,
,
;
,
,
;

 - контур, ограничивающий область
- контур, ограничивающий область
 ,
,
 ;
; - контур, образованный линиями
- контур, образованный линиями
 ,
,
 ;
; - контур, ограничивающий область
- контур, ограничивающий область
 ,
,
 ;
; - контур треугольника с вершинами
,
,
- контур треугольника с вершинами
,
,
 ;
; - контур треугольника с вершинами
- контур треугольника с вершинами
 ,
,
 ,
,
 ;
;
 - контур, образованный линиями
- контур, образованный линиями
 ,
,
 ;
; - контур, образованный линиями
,
- контур, образованный линиями
,
 ;
;- контур, образованный линиями
 ,
,
 ;
; - контур, образованный линиями
,
;
- контур, образованный линиями
,
;

- контур, образованный линиями
 ,
,
 .
.
Найти функцию по её полному дифференциалу:






















