X f*(X)

Рис3.1

3. Построим гистограмму равновероятностным способом.

Для построения гистограммы составим интервальный статистический ряд, учитывая что частота попадания СВ X в в каждый j-ый интервал должна быть одинаковая

Интервальный статистический ряд

j	Aj	Bj	hj	vj	pj*	fj*
1	0.01	0.1	0.09	10	0,1	1.1111
2	0.1	0.28	0.18	10	0,1	0.5556
3	0.28	0.43	0.15	10	0,1	0.6667
4	0.43	0.57	0.145	10	0,1	0.6897
5	0.57	0.69	0.11	10	0,1	0.9091
6	0.69	0.88	0.195	10	0,1	0.5128
7	0.88	1.19	0.315	10	0,1	0.3175
8	1.19	1.46	0.27	10	0,1	0.3704
9	1.46	2.09	0.625	10	0,1	0.16
10	2.09	3.33	1.240	10	0,1	0.0806

X f*(X)

Рис 4.1

3. Вычислим точечные оценки математического ожидания и дисперсии:

3. Вычислим интервальные оценки математического ожидания и дисперсии (γ = 0,95):

7. По виду графика эмпирической функции распределения 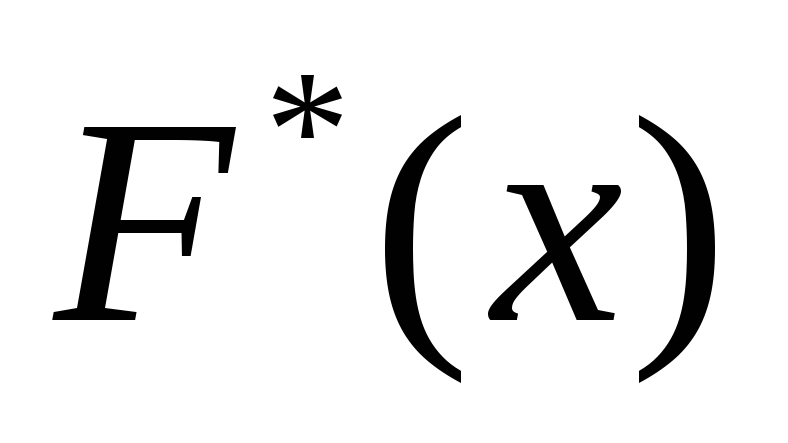и гистограмм выдвигаем двухальтернативную гипотезу о законе распределения случайной величины X:

H₀ – величина X распределена по экспоненциальному закону:

H₁ – величина X не распределена по экспоненциальному закону

Таким образом получаем полностью определенную гипотетическую функцию распределения:

Проверим гипотезу о экспоненциальном законе по критерию Пирсона . Вычислим значение критерияна основе равноинтервального статистического ряда:

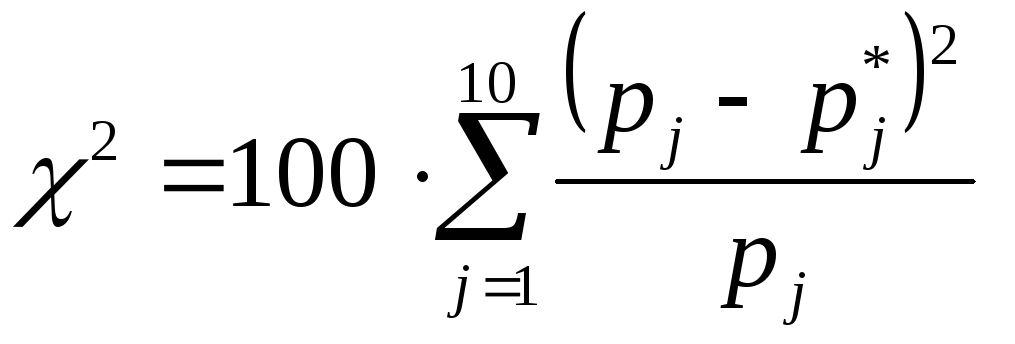
Теоретические вероятности попадания в интервалы вычислим по формуле:

Результаты расчётов

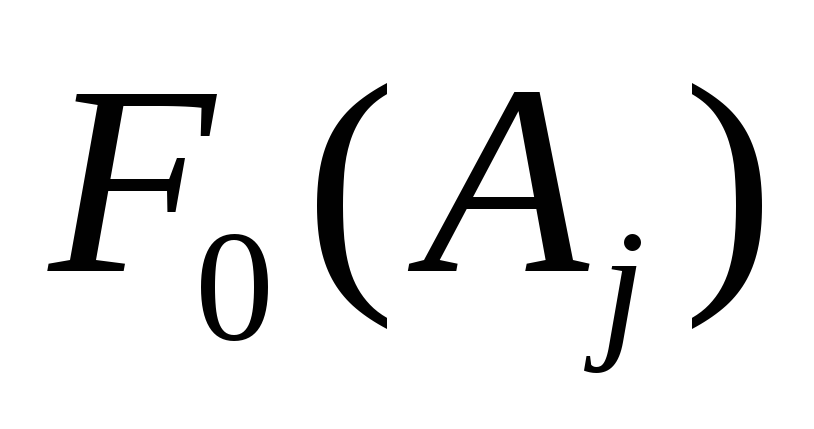
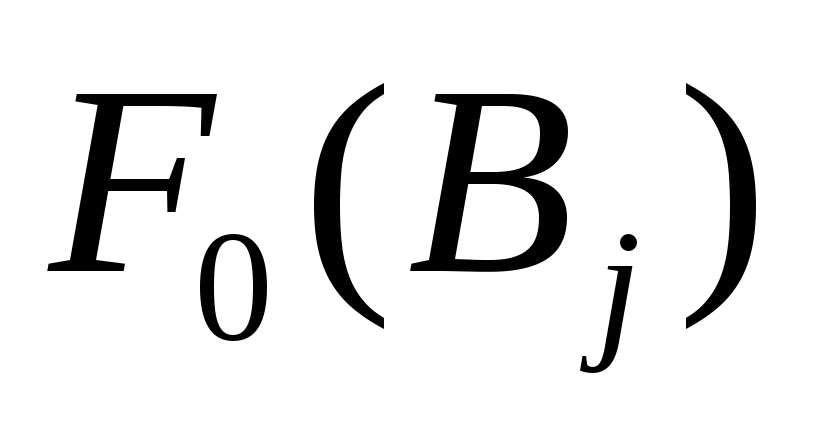
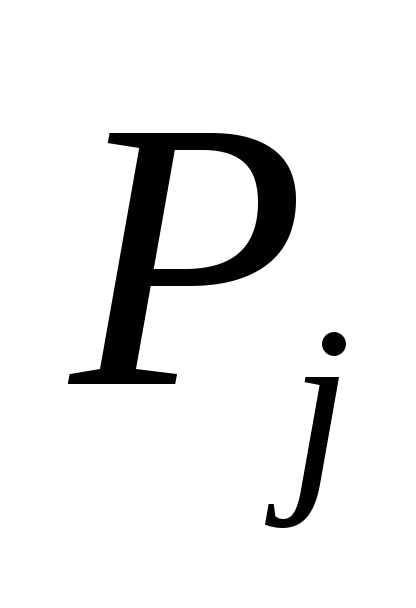
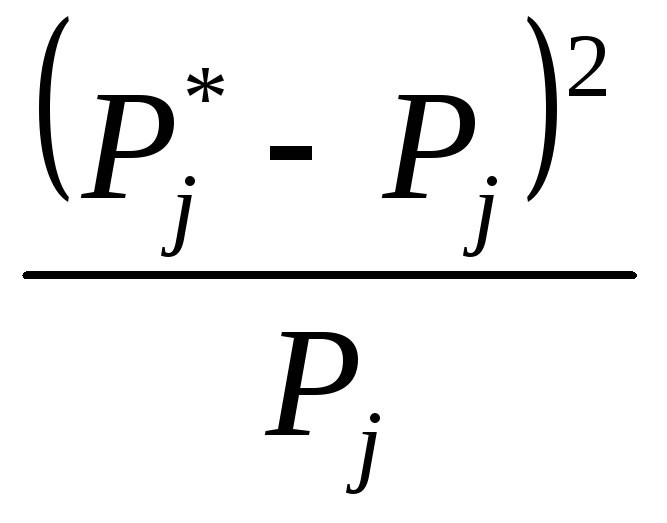
1	0	0,34	0,0000	0,3095	0,3095	0,25	0,01143
2	0,34	0,67	0,3095	0,5180	0,2085	0,24	0,00475
3	0,67	1,01	0,5180	0,6635	0,1455	0,17	0,00411
4	1,01	1,34	0,6635	0,7651	0,1016	0,1	0,00003
5	1,34	1,67	0,7651	0,8361	0,0709	0,08	0,00116
6	1,67	2,00	0,8361	0,8856	0,0495	0,05	0,00000
7	2,00	2,33	0,8856	0,9201	0,0346	0,05	0,00690
8	2,33	2,67	0,9201	0,9442	0,0241	0,02	0,00070
9	2,67	3,00	0,9442	0,9611	0,0168	0,02	0,00059
10	3,00	100	0,9611	1,0000	0,0389	0,02	0,00920
Сумма:					1	1	0,0389

Проверим правильность вычислений :

Вычислим критерий Пирсона:

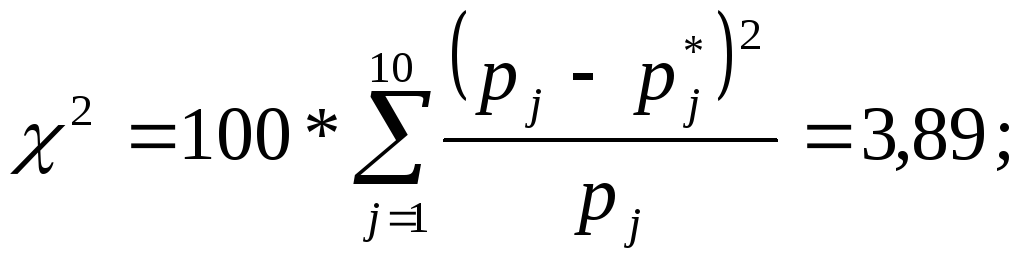
Определим число степеней свободы:

Выбираем критическое значения критерия Пирсона из таблицы для степени свободы и заданного уровня значимости :

Так как условие выполняется, то гипотеза H₀ об экспоненциальном законе распределения принимается (нет оснований ее отклонить).

8) Проверим гипотезу при помощи критерия Колмогорова. Для этого построим график гипотетической функции распределения в одной системе координат с эмпирической функцией(рисунок 2.1).

В качестве опорных точек используем 10 значений из таблицы расчетов в пункт 7. По графику определим максимальное по модулю отклонение между функциямии:

Вычислим значение критерия Колмогорова:

Из таблицы Колмогорова по заданному уровню значимости выбираем критическое значение критерия:

Так как условие выполняется, гипотеза H­₀ о экспоненциальном законе распределения принимается (нет оснований ее отклонить).