КР(1)

1. Подбрасываются две игральные кости. Определить вероятность того, что сумма выпавших чисел равна восьми.

Решение: Равновозможными элементарными исходами здесь являются пары (x, y), где x и y принимают значения: 1,2,3,4,5,6. Таким образом, общее число элементарных исходов равно n = 6 * б = 36.

Событию А благоприятствуют пары (2;4), (3;5), (4;4), (5;3), (4;2), число которых равно m = 5.

Следовательно, Р(А) = m/n = 5/36.

Ответ: 5/36.

2.Отказ любого из элементов приводит к прерыванию сигнала в той ветви цепи, где находится данный элемент. Вероятности отказа элементов 1, 2, 3, 4, 5 соответственно равны p1=0,1; p2=0,2; p3=0,3; p4=0,4; p5=0,5. Найти вероятность того, что сигнал пройдет со входа на выход.

Решение:

3.7. Один из трех стрелков вызывается на линию огня и производит выстрел. Цель поражена. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3 , для второго - 0,5 , для третьего - 0,8. Найти вероятность того, что выстрел произведен вторым стрелком.

Решение: Возможны три гипотезы:

- на линию огня вызван первый стрелок,

- на линию огня вызван второй стрелок,

- на линию огня вызван третий стрелок.

Так как вызов на линию огня любого стрелка равновозможен, то

В результате опыта наблюдалось событие В - после произведенного выстрела мишень поражена. Условные вероятности этого события при сделанных гипотезах равны:

По формуле Байеса вероятность гипотезы после опыта:

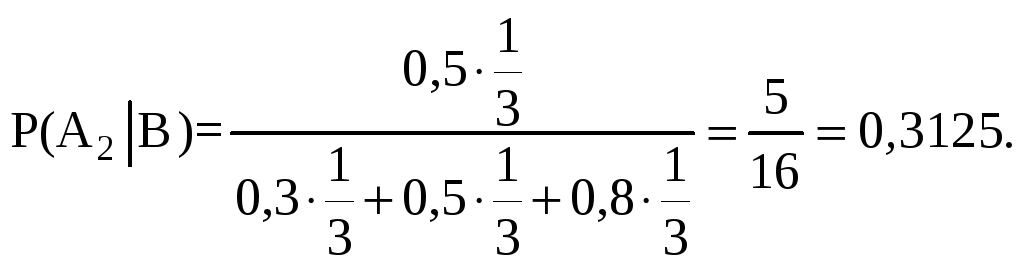
Ответ: 0,3125.

4.10. Вероятность появления события А в каждом из 15 независимых опытов равна 0,3. Определить вероятность появления события А семь или восемь раз.

Решение

Локальная приближенная формула Лапласа. При больших n имеет место приближенное равенство

,

где , .

; j(1,4) » 0,2468;

Р₁₅ (7) » ;

; j(1,97) » 0,0608;

Р₁₅ (8) » ;

Ответ: Р₁₅ (7) »0,138; Р₁₅ (8) »0,034.

5.12

В задачах 5.1-5.30 дискретная случайная величина Х может принимать одно из пяти фиксированных значений x1, x2, x3, x4, x5 с вероятностями p1, p2, p3, p4, p5 соответственно (конкретные значения приведены в табл. 1.1). Вычислить математическое ожидание и дисперсию величины Х. Рассчитать и построить график функции распределения.

x	-1	0	1	2	3
p	0,6	0,1	0,1	0,1	0,1

Решение: находим математическое ожидание и

Теперь определяем дисперсию

Соответствующий данному ряду многоугольник распределения:

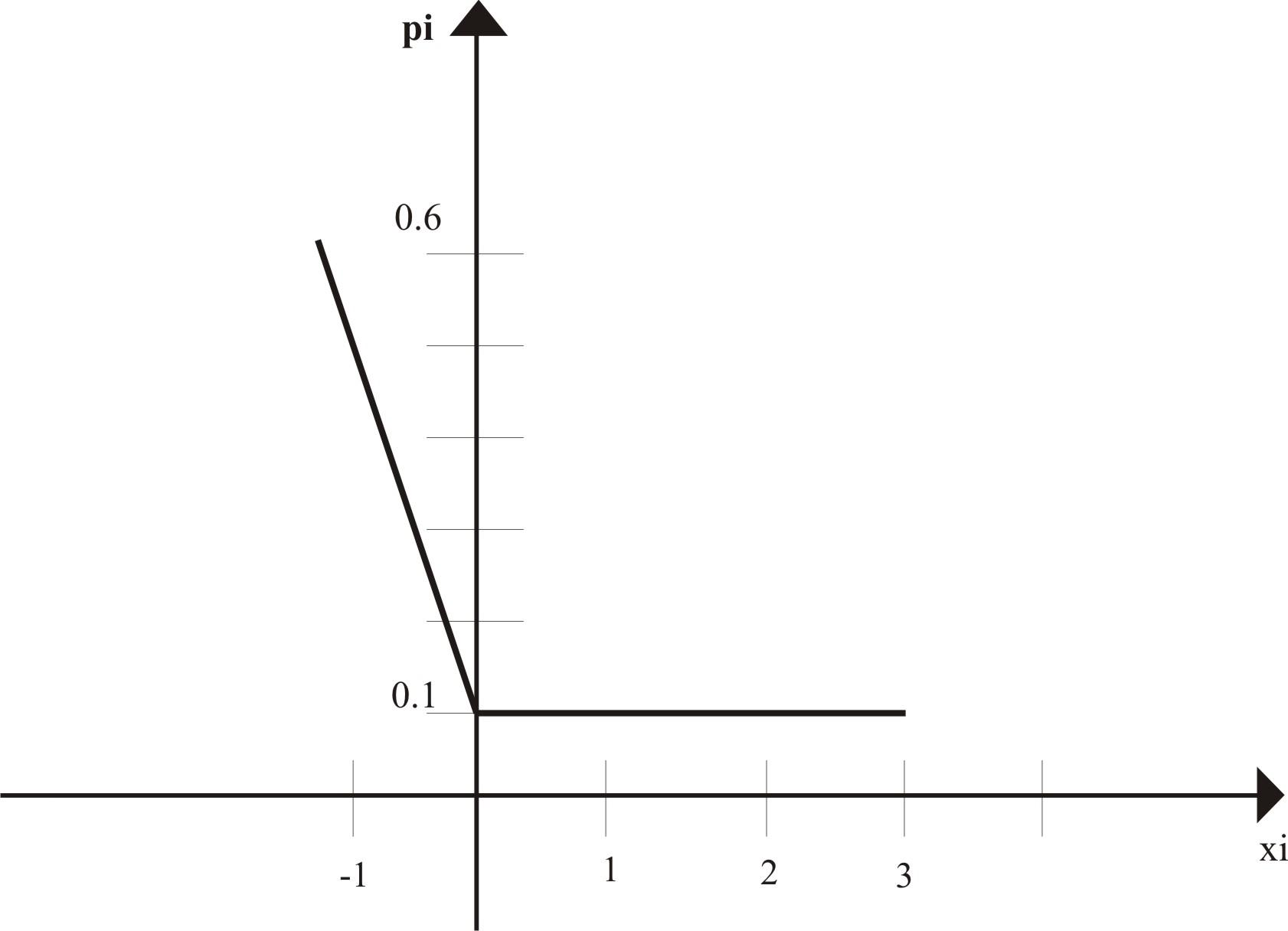
Чтобы построить функцию распределения разобьем ось на интервалы

На каждом из этих интервалов функция распределения будет постоянной:

График этой функции:

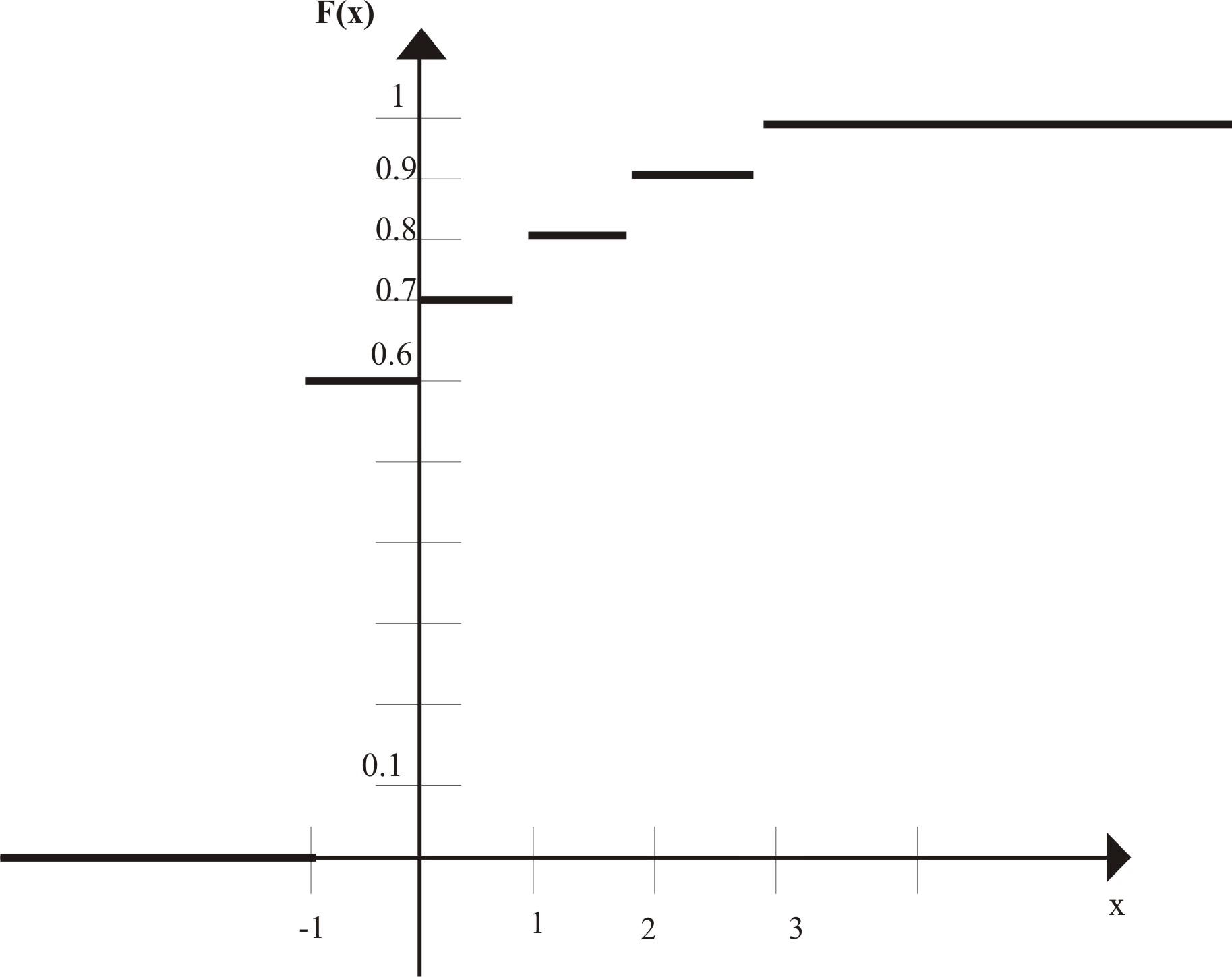
6.12

Случайная величина Х задана плотностью вероятности

Определить константу С, математическое ожидание, дисперсию, функцию распределения величины Х, а также вероятность ее попадания в интервал.

Решение: чтобы найти С, нужно воспользоваться свойством функции распределения:

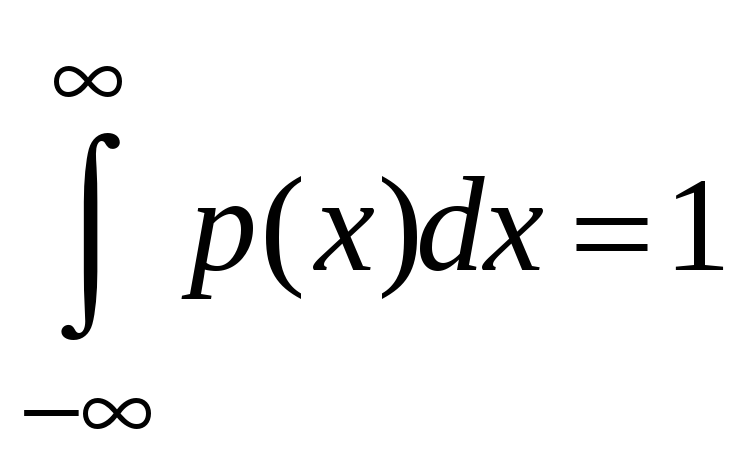
Находим

Математическое ожидание находим по формуле

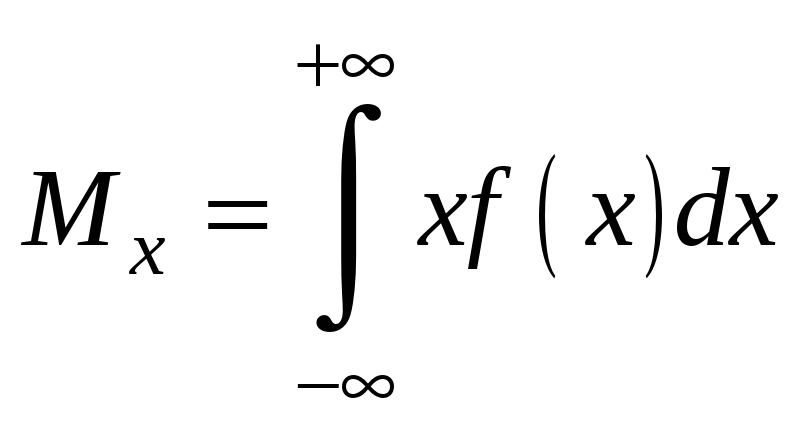
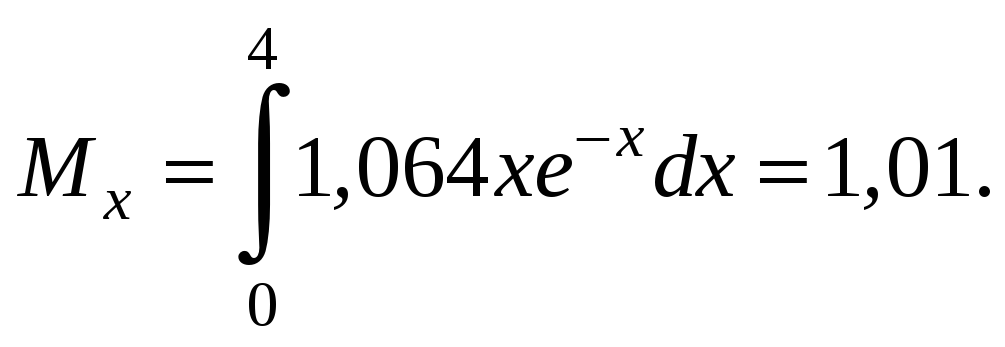
Дисперсию находим по формуле 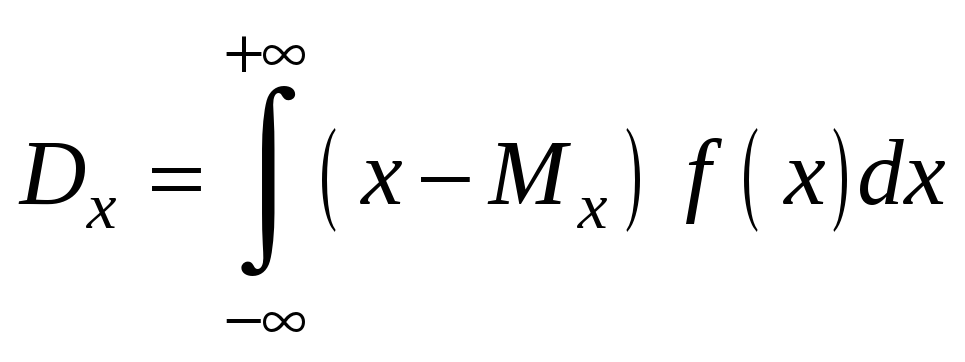равна

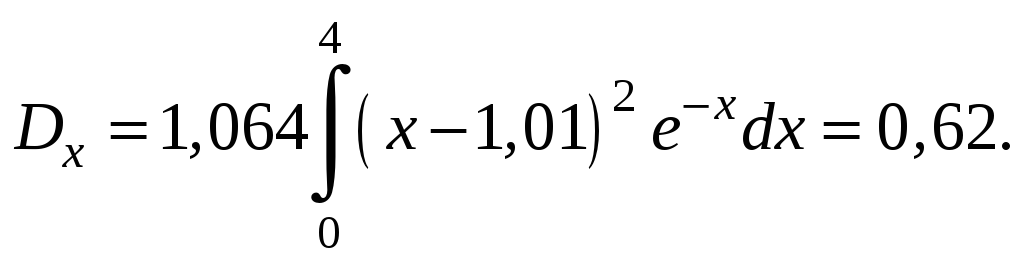
Так как плотность вероятности задана различными формулами на разных интервалах, то и функция распределения будем искать для каждого интервала отдельно:

для x<0

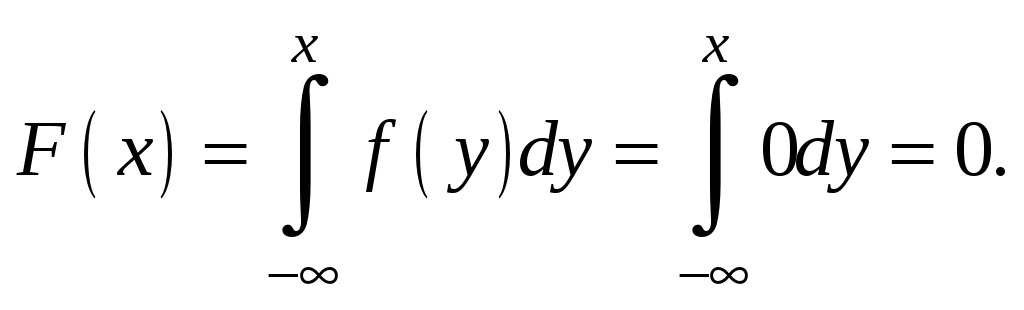
для

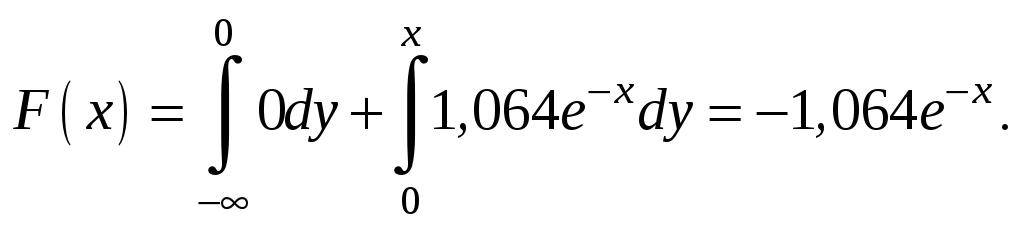
для х>4

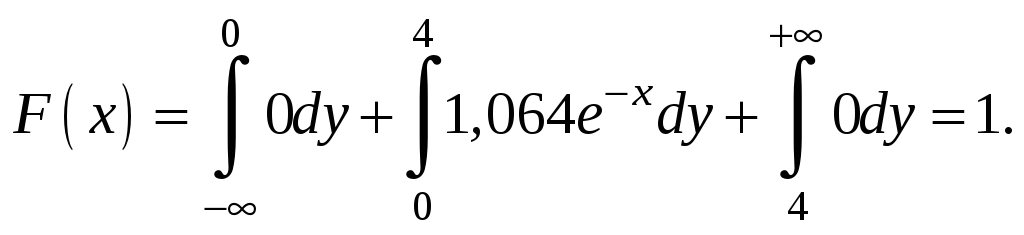
Окончательно имеем:

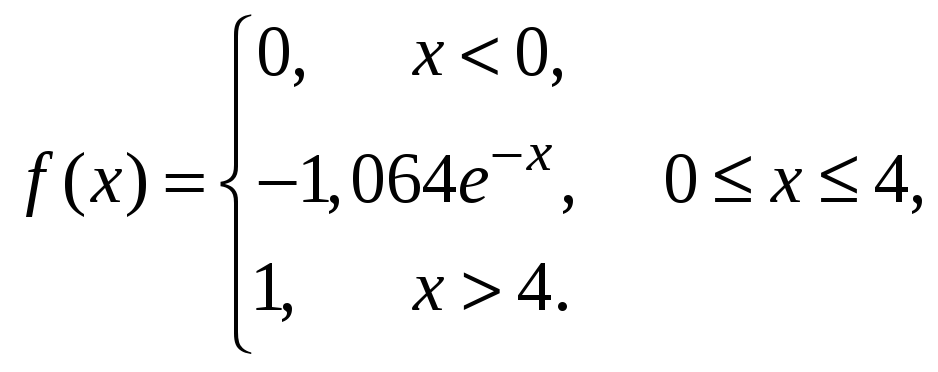
Вероятность

7.20

Случайная величина Х распределена равномерно на интервале [-1,2]. Построить график случайной величины и определить плотность вероятности g(y), .

Для равномерного распределения знаем f(x)=1/(b-a) = 1/3.

Так как Х равномерно распределена в интервале [-1,2], то ее плотность вероятности равно

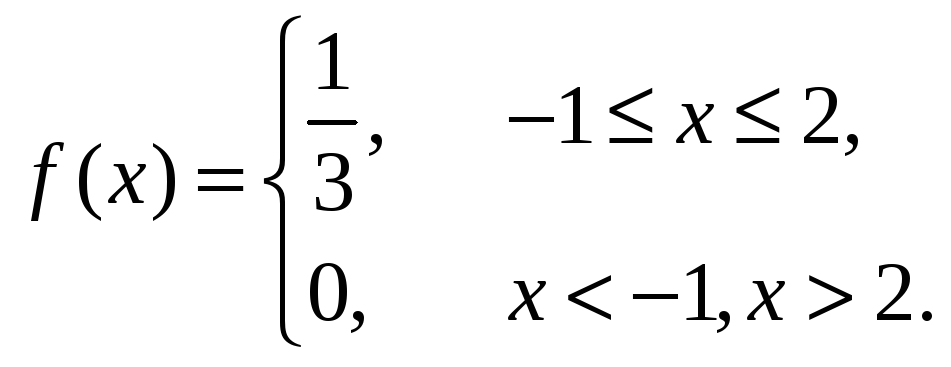
Построим график величины для х в интервале [-1,2] и в зависимости от числа k обратных функций выделим следующие интервалы Y:

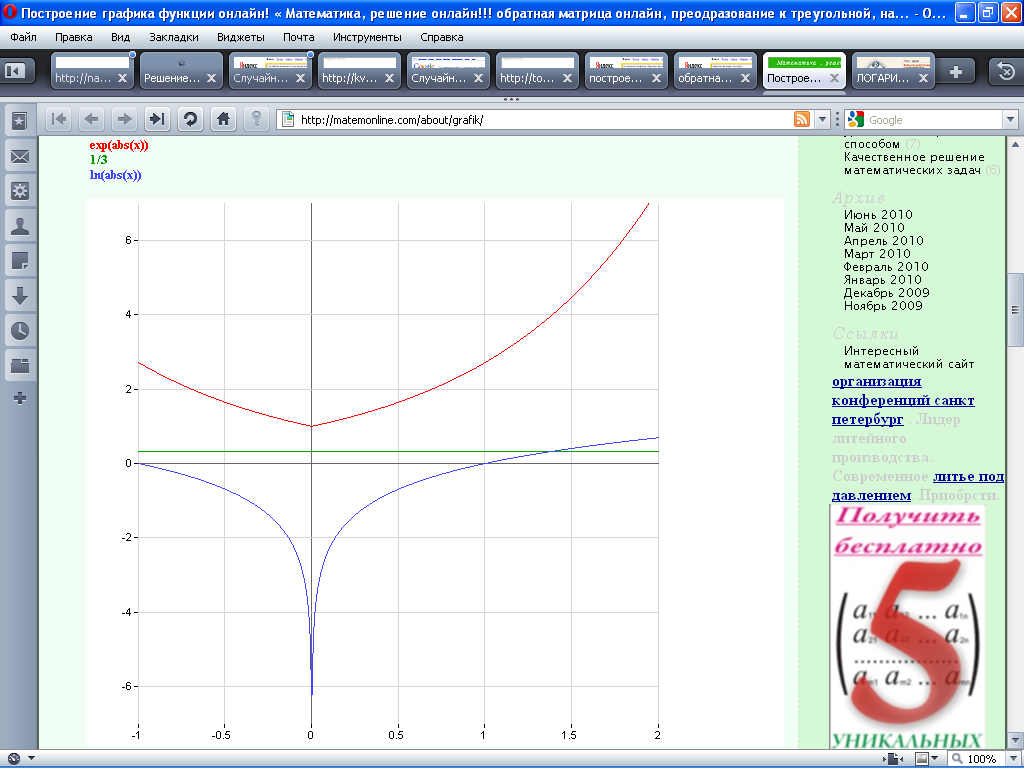
, Y=1/3,

Так как на интервалах и обратная функция не существует, то для этих интервалов g(y)=0.

В интервале две обратные функции

В интервале одна обратная функция , следовательно

Таким образом, плотность вероятности величины Y равна

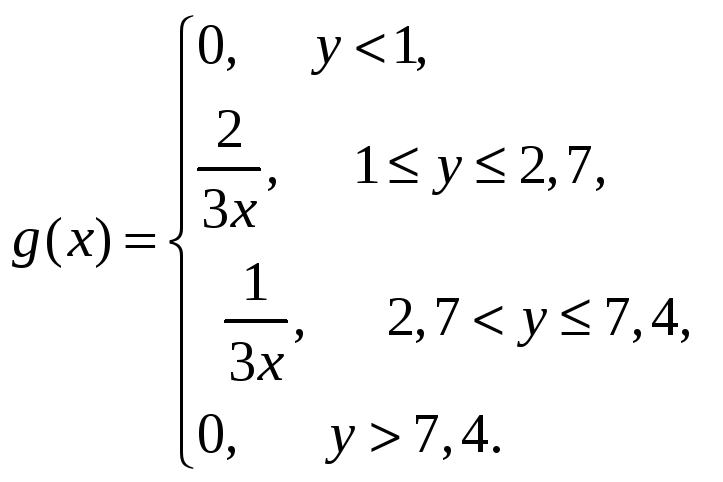
8.17

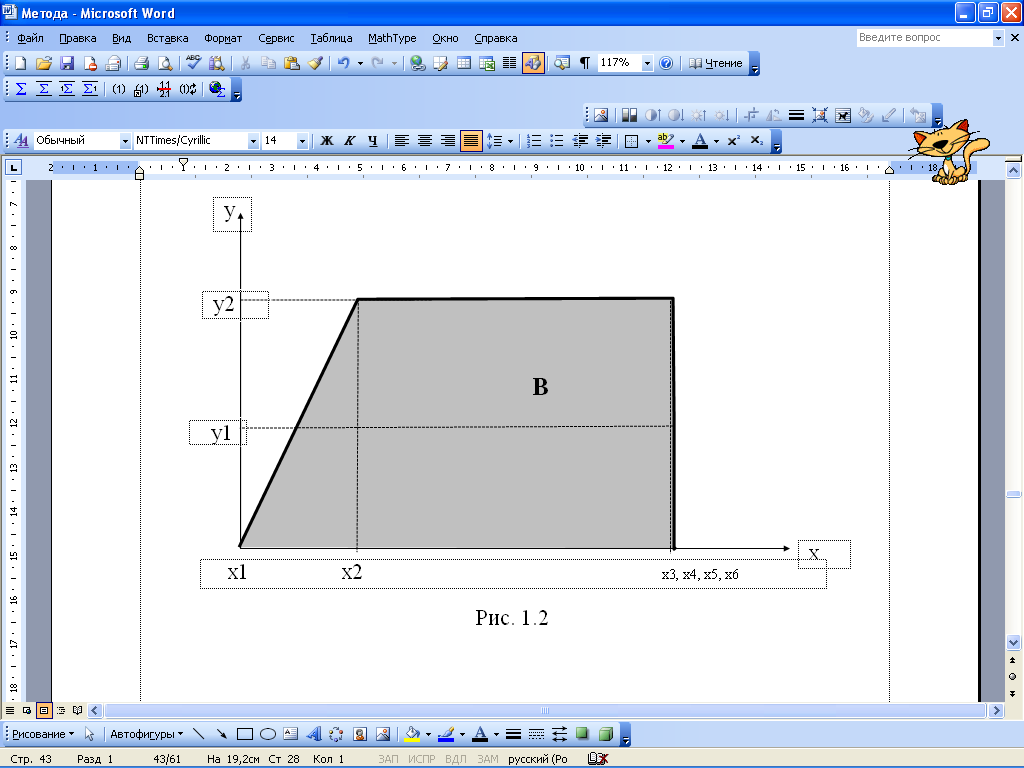
Двумерный случайный вектор (Х, У) равномерно распределен внутри выделенной жирными прямыми линиями на рис. 1.2 области B. Двумерная плотность вероятности f(x,y) одинакова для любой точки этой области B:

Вычислить коэффициент корреляции между величинами X и Y.

x1	x2	x3	x4	x5	x6	y1	y2
0	0	4	4	4	4	1	2

Решение: область В ограниченна прямыми: y=2,x=4,y=2x.

Запишем в аналитической форме совместную плотность вероятности:

Определим c, используя условие нормировки:

Найдем математическое ожидание и дисперсию величины X

,

.

Найдем математическое ожидание и дисперсию величины Y

Определим корреляционный момент K_xy

Коэффициент корреляции величин X и Y

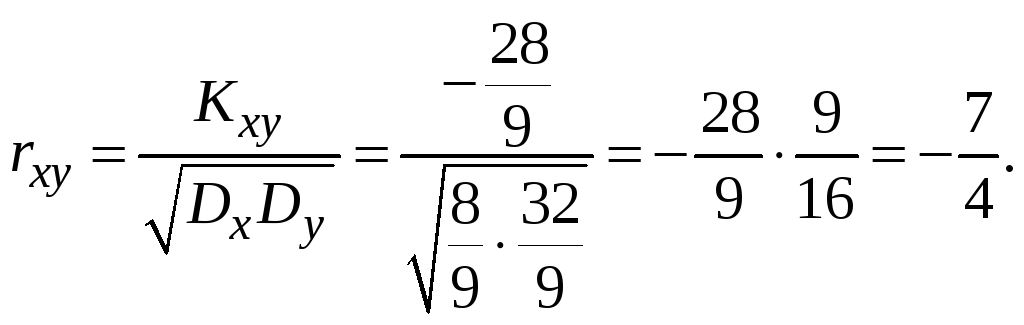
1. Одномерная выборка:

2.76 0.20 1.42 3.11 3.38 1.57 0.68 2.10 0.30 0.46 1.80 0.96 1.13 1.20 0.46 1.86 0.59 0.46 1.94 3.80 1.96 0.87 1.40

0.46 1.04 0.05 0.09 2.40 1.16 0.06 1.98 0.09 1.48 0.77 0.82 0.14 0.92 0.75 1.73 0.50 1.27 0.69 0.91 0.05 0.07 0.42

1.59 1.76 1.63 0.94 0.82 1.07 1.80 0.64 0.29 0.89 1.15 0.16 0.40 0.56 0.43 3.14 0.12 0.31 0.50 0.19 0.07 0.43 0.17

0.17 0.61 0.15 2.87 0.50 1.86 1.69 0.63 1.82 2.27 0.14 4.17 0.14 0.43 5.65 3.76 2.32 0.80 0.08 3.96 0.05 1.58 2.52

0.01 0.28 1.86 0.08 0.76 2.01 0.13 0.10

Вариационный ряд выборки:

1. 0.05 0.05 0.05 0.06 0.07 0.07 0.08 0.08 0.09 0.09 0.10 0.12 0.13 0.14 0.14 0.14 0.15

0.16 0.17 0.17 0.19 0.20 0.29 0.30 0.31 0.40 0.42 0.43 0.43 0.43 0.46 0.46 0.46 0.46 0.47 0.50 0.50 0.50 0.56 0.59 0.61 0.63 0.64 0.68 0.69 0.75 0.76 0.77 0.80 0.82 0.82 0.87 0.89 0.91 0.92 0.94 0.96 1.04 1.07 1.13 1.15 1.16 1.20 1.27 1.40 1.42 1.48 1.57 1.58 1.59 1.63 1.69 1.73 1.76 1.80 1.80 1.82 1.86 1.86 1.86 1.94 1.96 1.98 2.01 2.10 2.27 2.32 2.40 2.52 2.76 2.87 3.11 3.14 3.38 3.76 3.80 3.96 4.17 5.65

Построим интервальный статистический ряд:

Определим длину интервала:

Определим границы интервалов разбиения

; ;

Построим интервальный статистический ряд:

Сi, Сi+1		(-0,36;0,38)		[0,38;1,12)		[1,12;1,86)		[1,86;2,6)		[2,6;3,34)		[3,34;4,08)		[4,08;4,82)		[4,82;5,56)	[5,56;6,3)
		0,01		0,75		1,49		2,23		2,97		3,71		4,45		5,19	5,93
		26		34		18		12		4		4		1		0	1
	0,26		0,34		0,18		0,12		0,04		0,04		0,01		0		0,01

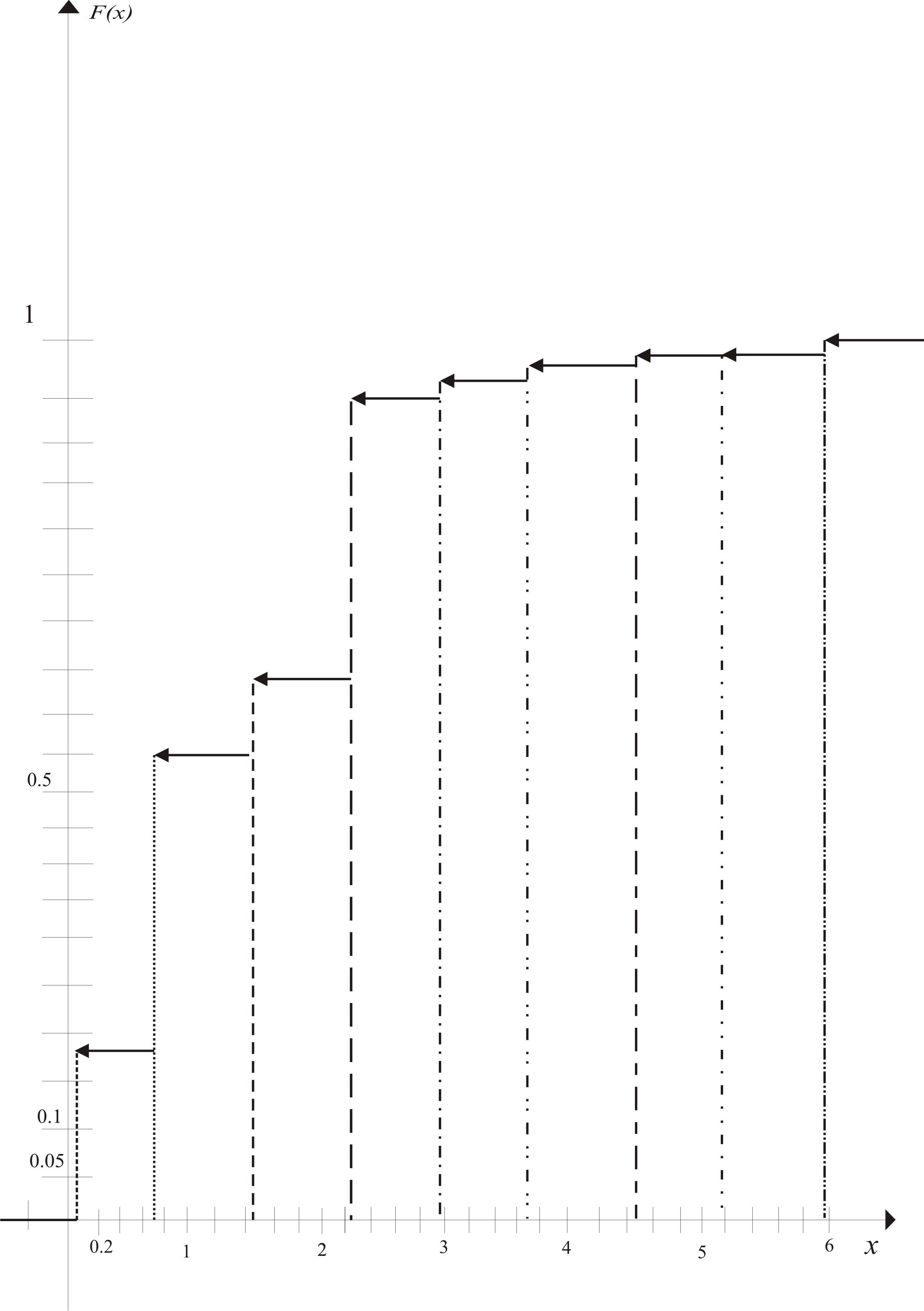
Для построения эмпирической функции распределения воспользуемся соотношением:

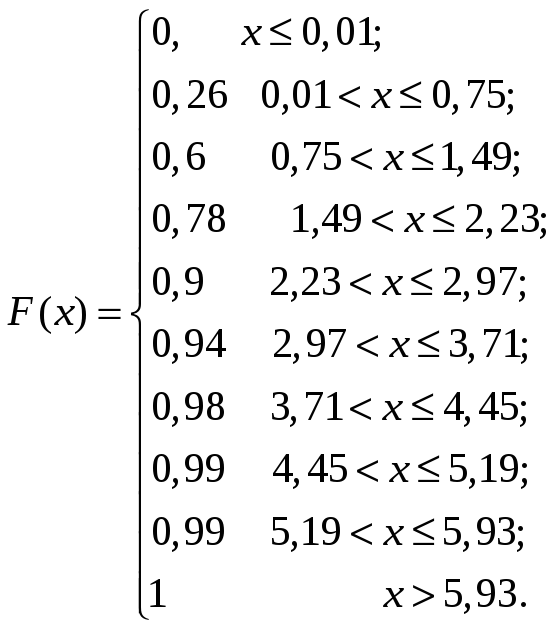
Объем выборки равен 100. Количество интервалов определяем по формуле:

Для интервального метода построения интервального статистического ряда вероятностей величины:

1	0,01	0,574	0,564	40	0,71
2	0,574	1,138	0,564	25	0,44
3	1,138	1,702	0,564	8	0,14
4	1,702	2,266	0,564	13	0,23
5	2,266	2,83	0,564	5	0,09
6	2,83	3,394	0,564	4	0,07
7	3,394	3,958	0,564	2	0,035
8	3,958	4,522	0,564	2	0,035
9	4,522	5,086	0,564	0	0
10	5,086	5,65	0,564	1	0,018

Равноинтервальная гистограмма

Для равновероятностного метода построения интервального статистического ряда вероятностей величины рассчитываем:

1	0,01	0,09	0,08	10	0,1	1,25
2	0,09	0,17	0,08	10	0,1	1,25
3	0,17	0,43	0,26	10	0,1	0,385
4	0,43	0,575	0,145	10	0,1	0,67
5	0,575	0,81	0,235	10	0,1	0,425
6	0,81	1,1	0,29	10	0,1	0,345
7	1,1	1,585	0,485	10	0,1	0,206
8	1,585	1,86	0,275	10	0,1	0,36
9	1,86	2,64	0,78	10	0,1	0,13
10	2,64	5,65	3,01	10	0,1	0,03

Равновероятностная гистограмма

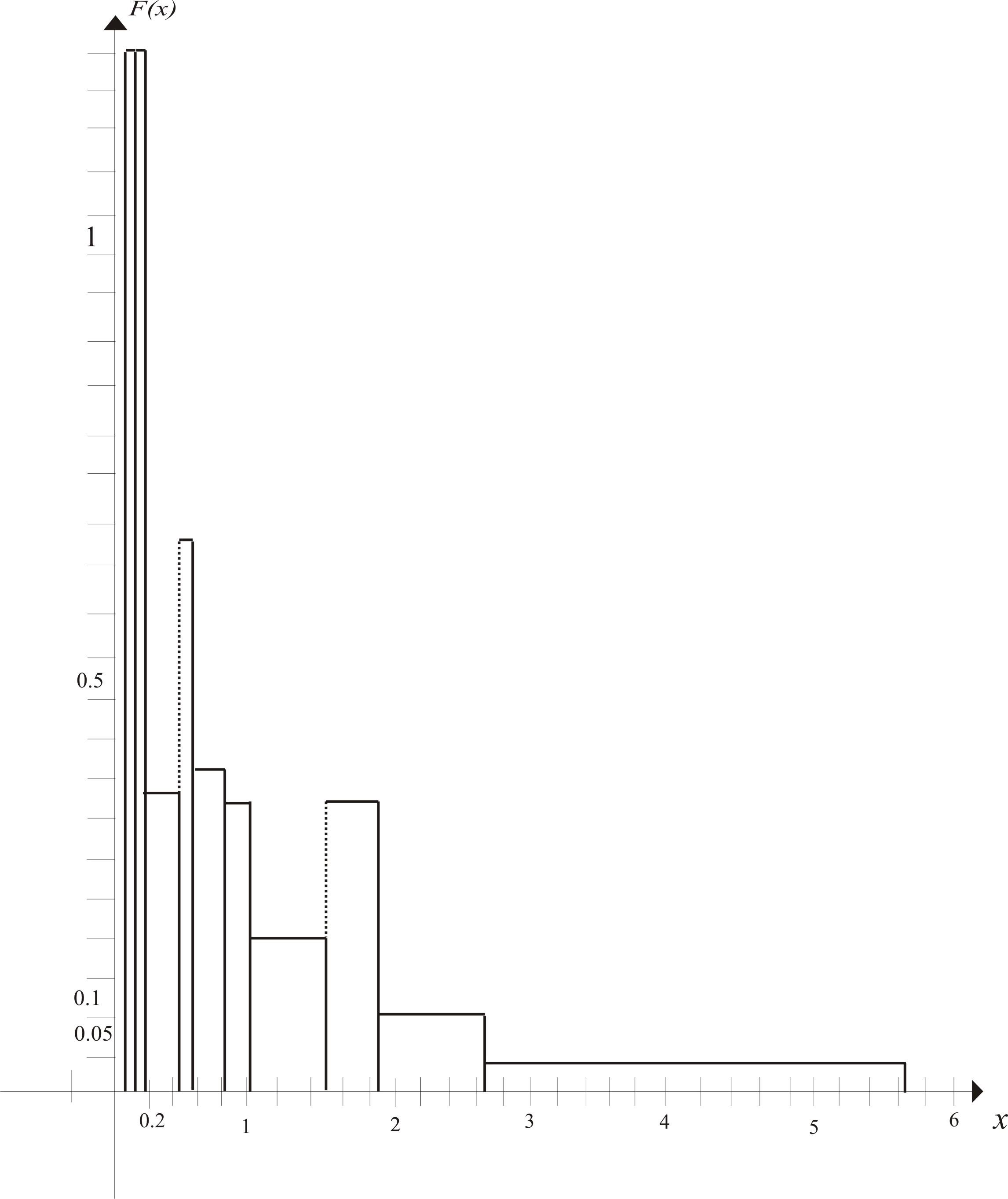
По виду гистограмм выдвигаем гипотезу о том, что случайная величина Х распределена по нормальному закону:

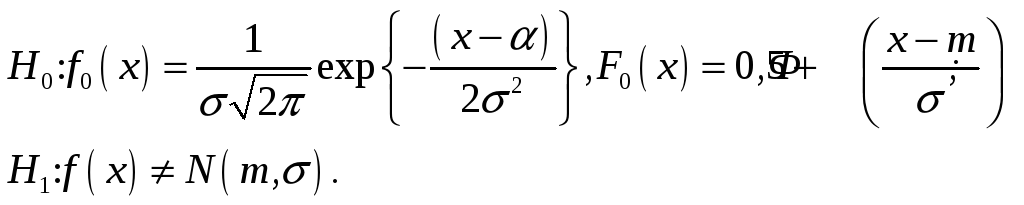
Используя метод моментов, определим оценки неизвестных параметров и гипотетического (нормального) закона распределения:

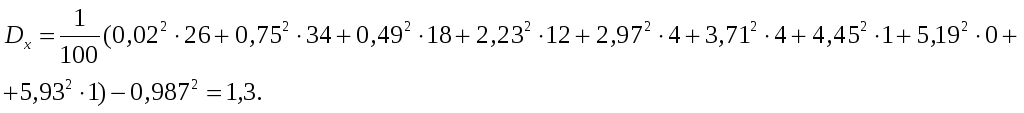
Значение критерия вычисляем по формуле:

При проверке гипотезы используем равновесную гистограмму. В этом случае:

Теоретически вероятность рассчитывается:

,,,,,,,

Тогда

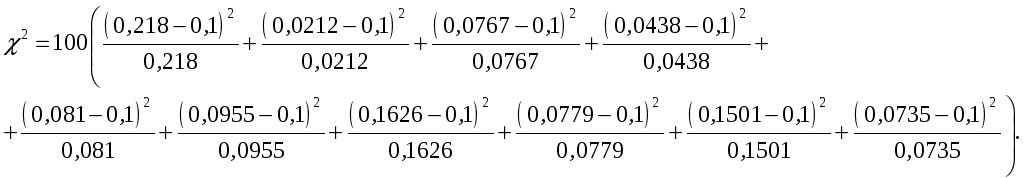
После этого из таблицы распределения выбираем критическое значение

Так как , то гипотеза не принимается.

Используя критерий Колмогорова, проверим гипотезу о том, что случайная величина распределена по нормальному закону (необходимые нам параметры: , )

Ясно, что максимальное отклонение эмпирической функции распределения от непрерывной функции распределения достигается в точках скачков функции

Будем считать, что в точками скачков функции являются - середины интервалов интервального вариационного ряда (j = 1,2,….,8).

Тогда

Так как по предположению случайная величина распределена нормально с параметрами 0,987 и 1,14 , то где - функция Лапласа.

1	0,38	0,26	-0,2019	0,2981	0,038
2	1,12	0,6	0,116	0,616	0,016
3	1,86	0,78	0,276	0,776	0,004
4	2,6	0,9	1,415	0,921	0,021
5	3,34	0,94	2,064	0,9803	0,04
6	4,08	0,98	2,713	0,9966	0,0166
7	4,82	0,99	3,362	0,99952	0,00952
8	5,56	0,99	4,011	0,999968	0,009968