Билет 17. Дб- и сдб-деревья.

ДБ-дерево.

Максимальное количество ключей на странице – 2, ссылки могут быть не только вертикальными, но и горизонтальными. Реализация:

struct DBTree {

Tdata data;

struct DBTree *left;

struct DBTree *right;

bool h;

}

Схемы включения в ДБ-дерево:

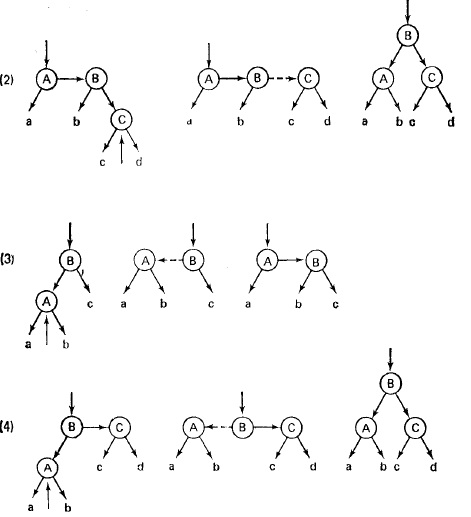
СДБ-дерево.

Возможность делать ссылки в обе стороны.

Свойства:

• Каждая вершина имеет 1 ключ и не более 2 ссылок на поддеревья.

• Ссылки могут быть вертикальными и горизонтальными. Нет ни одного пути поиска с 2 подряд идущими ссылками. Все листья находятся на одном уровне.

Реализация:

struct SDBTree {

Tdata data;

struct DBTree *left;

struct DBTree *right;

bool hr;

bool hl;

}

Операция вставки:

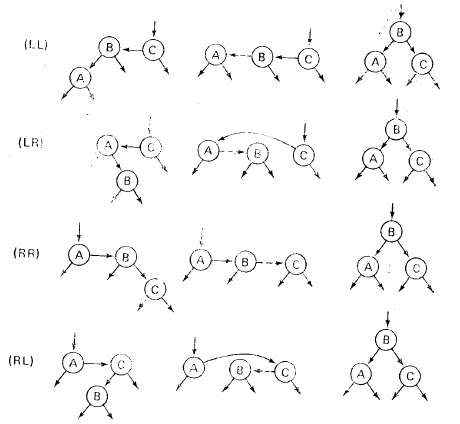
Билет 18. Характеристики сбалансированных деревьев.

• Дерево поиска

+ Простота операций вставки, удаления, поиска

- Несбалансированное

• Идеально сбалансированное дерево

+Идеально сбалансированно, О(log₂n)

- Нет операций вставки и удаления

• АВЛ-сбалансированное дерево

+ Операции поиска, вставки и удаления проводятся за О(log n)

- Необходима балансировка после каждой операции

• Красно-черные деревья (=СДБ)

Аналог АВЛ с некоторыми изменениями

• Б-дерево

+ Возможность создания больших деревьев

• ДБ-дерево

- Хуже, чем СДБ

• Дерево оптимального поиска

+ Оптимальный поиск при различных вероятностях ключей

- Нет операций вставки и удаления, сложность построения О(n²)

• Splay-дерево

+ Сбалансированно

Время О(log n)

Билет 19. Дерево оптимального поиска.

Бывают случаи, когда информация о вероятности появления ключа известна. В таких случаях для сокращения времени необходимо использование таких деревьев, в которых самые часто встречающие вершины находились бы ближе к корню дерева. Предположим, что в дереве поиска вероятность обращения к ключу i равна . Мы хотим организовать дерево поиска так, чтобы полное число шагов поиска – для достаточно большого числа попыток – было минимальным. Для этого изменим определение длины пути, приписывая каждому узлу некоторый вес и считая, что корень находится на уровне 1, а не 0, поскольку с ним связано первое сравнение на пути поиска. Узлы, к которым обращений много, становятся тяжелыми, а те, которые посещаются реже – легкими. Тогда взвешенная длина путей (внутренних) равна сумме всех путей из корня до каждого узла, взвешенных с вероятностью обращения к этому узлу: .

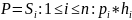Обнаружение того факта, что некий ключ k не является ключом в дереве поиска, можно рассматривать как обращение к так называемому дополнительному узлу, вставленному между ближайшими меньшим и большим ключами. Если вероятность q_i появления такого ключа известна, то можно изменить формулу для взвешенного пути, включая туда и безуспешные поиски: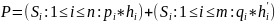 . В этом случае взвешенную длину пути называют ценой дерева поиска. Дерево поиска с минимальной ценой среди всех деревьев с заданным набором ключей и соответствующими вероятностями, называется оптимальным деревом.

Пусть a_i – количество поисков ключа k_i, а b_i – количество поисков ключа k_i < x < k_i+1

Средний взвешенный путь: , где n – число вершин, m – число псевдо вершин.