2.3 Принцип суперпозиции.

Принцип суперпозиции, принцип наложения (принцип линейности), 1) допущение, согласно которому если составляющие сложного процесса воздействия взаимно не влияют друг на друга, то результирующий эффект будет представлять собой сумму эффектов, вызываемых каждым воздействием в отдельности. Принцип суперпозиции строго применим к системам, поведение которых описывается линейными соотношениями (так называемые линейные системы).

Классическое электромагнитное поле в вакууме удовлетворяет принципу суперпозиции: сумма любого числа физически реализуемых полей есть тоже физически реализуемое электромагнитное поле. В силу принципа суперпозиции электромагнитное поле, созданное совокупностью электрических зарядов и токов, равно сумме полей, создаваемых этими зарядами и токами по отдельности.

В классической физике принцип суперпозиции - приближённый принцип, вытекающий из линейности уравнений движения соответствующих систем (что обычно является хорошим приближением для описания реальных систем), например, уравнений Максвелла для электромагнитного поля. Таким образом, он вытекает из более глубоких динамических принципов и поэтому не является фундаментальным. Он и не универсален. Так, макроскопическое электромагнитное поле в веществе, строго говоря, не подчиняется принципу суперпозиции в силу зависимости (иногда существенной) диэлектрической и магнитной проницаемостей от внешнего поля (например, в ферромагнетике) и т. д.

2.4 Преобразование полей Е и B.

Преобразование Лоренца (буст вдоль оси x¹) электромагнитного поля.

E`<sub>1</sub> = E<sub>1</sub>; E`₂ = (E₂ B₃); E`₃ = (E₃ + B₂);

B`<sub>1</sub> = B<sub>1</sub>; B`₂ = (B₂ + ₃); B`₃ = (B₃ ₂)

*2.5 Понятие о 4-тензоре напряженности электромагнитного поля F^.

F_ = _A__A_,

F_= (E, B) = ;

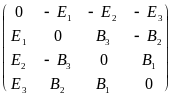F^_= (E, B) = ;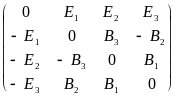

F^_ ;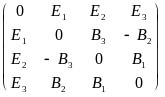

F_^_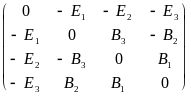

2.6 Плотность энергии и плотность потока энергии электромагнитного поля.

Объемная плотность энергии электромагнитного поля в линейной изотропной среде равна сумме объемных плотностей энергии электрического и магнитного полей

w_em = ED/2 + HB/2. [Дж/м³]

Величина вектора плотности потока энергии (вектор Пойнтинга) определяется соотношение

S = wv = EH.

Вектор плотности потока энергии S направлен в сторону распространения энергии, а его модуль равен энергии, переносимой за единицу времени, через единичную площадку, перпендикулярную направлению распространения. S измеряется в Дж/(см²)=Вт/м².

В общем случае

S = wu.

где u - скорость переноса энергии или групповая скорость.

3 Скалярный и 3-векторный потенциал A.

Потенциалы электромагнитного поля, величины, характеризующие электромагнитное поле.

3.1 Определение скалярного и 3-векторного потенциалов электромагнитного поля. Калибровки.

Скалярный потенциал электрического поля - энергетическая характеристика электрического поля - скалярная величина, равная отношению потенциальной энергии заряда в поле к величине этого заряда. В СИ потенциал электрического поля измеряется в вольтах.

В электростатике векторное электрическое поле можно характеризовать одной скалярной функцией — электростатическим потенциалом.

В общем случае для описания произвольного электромагнитного поля вместо двух векторов — магнитной индукции В и напряжённостью электрического поля E можно ввести две другие. величины: векторный потенциал А (r, t) и скалярный потенциал (r, t) (где r — радиус-вектор, t — время), при этом В и Е однозначно выражаются через А и 

В = А,

E =  A/t.

Уравнения для потенциалов поля имеют более простую форму, чем исходные уравнения Максвелла, и поэтому введение потенциалов электромагнитного поля упрощает задачу нахождения переменных электромагнитных полей. Существенное упрощение уравнений для потенциалов возможно благодаря тому, что потенциалы определяются неоднозначно. Если вместо А и  выбрать новые потенциалы

А' = А + ,

´=  t

где  — произвольная функция координат и времени, то векторы В и Е не изменятся. Инвариантность электромагнитного поля по отношению к преобразованиям потенциалов носит название калибровочной или градиентной инвариантности. Калибровочная инвариантность позволяет наложить на потенциалы электромагнитного поля. дополнительное условие. Обычно таким дополнительным условием является условие Лоренца:

A +c^-1t,

где  и — диэлектрическая и магнитная проницаемости среды. При использовании лоренцевой калибровки уравнения для потенциалов электромагнитного поля в однородной среде ( = const,  = const), получаемые из уравнений Максвелла, приобретают одинаковую форму:

( v^2²/t²) = /₀.

(  v^2²/t²)A = ₀j.

здесь  — оператор Лапласа,  и j — плотности заряда и тока, a v = с/()^1/2 — скорость распространения электромагнитного поля в среде. 

Уравнения для потенциалов электромагнитного поля позволяют определить потенциалы А и  по известному распределению зарядов и токов, а следовательно, характеристики электромагнитного поля В и Е.

3.2 Скалярный потенциал неподвижного точечного заряда.

(r) = kq/r. [В]

k = 1/₀ ≈ 910⁹ м/Ф.

3.3 Векторный потенциал плотности тока.

(r) = ₀j/4r. [Тлм = Вс/м]

при калибровке = 0.

3.4 Принцип суперпозиции.

*3.5 Понятие о 4-векторном потенциале. Преобразование 4-векторного потенциала.

A^= (A⁰, A¹, A², A³) = (A)_c=1 = (/cA)_c1

A_= (A₀, A₁, A₂, A₃) = (A⁰, A¹, A², A³) =

= (A)_c=1 = (/cA)_c1.

Преобразование Лоренца (буст вдоль оси x¹).

^_

4 Полевые уравнения классической электродинамики (полевые уравнения Максвелла).

Уравнения Максвелла, фундаментальные уравнения классической макроскопической электродинамики, описывающие электромагнитные явления в произвольной среде.

Сформулированы Дж. К. Максвеллом (1860-е) на основе обобщения эмпирических законов электрических и магнитных явлений.

Опираясь на эти законы и развивая идею М. Фарадея о том, что взаимодействия между электрически заряженными телами осуществляются посредством электромагнитного поля, Максвелл создал теорию электромагнитных процессов, математически выражаемую уравнениями Максвелла.

Современная форма уравнений Максвелла дана Генрихом Герцем () и Оливером Хевисайдом ().

Уравнения Максвелла связывают величины, характеризующие электромагнитное поле, с его источниками, то есть с распределением в пространстве электрических зарядов и токов.

В пустоте электромагнитное поле характеризуется двумя векторными величинами, зависящими от пространственных координат и времени: напряжённостью электрического поля Е и магнитной индукцией В.

Эти величины определяют силы, действующие со стороны поля на заряды и токи, распределение которых в пространстве задаётся плотностью заряда  (зарядом в единице объёма) и плотностью тока j (зарядом, переносимым в единицу времени через единичную площадку, перпендикулярную направлению движения зарядов). Для описания электромагнитных процессов в материальной среде (в веществе), кроме векторов Е и В, вводятся вспомогательные векторные величины, зависящие от состояния и свойств среды: электрическая индукция D и напряжённость магнитного поля Н.

Уравнения Максвелла позволяют определить основные характеристики поля (Е, В, D и Н) в каждой точке пространства в любой момент времени, если известны источники поля j и  как функции координат и времени.

Уравнения Максвелла могут быть записаны в интегральной или в дифференциальной форме.

Уравнения Максвелла в интегральной форме определяют по заданным зарядам и токам не сами векторы поля Е, В, D, Н в отдельных точках пространства, а некоторые интегральные величины, зависящие от распределения этих характеристик поля: циркуляцию векторов Е и Н вдоль произвольных замкнутых контуров и потоки векторов D и B через произвольные замкнутые поверхности.

Порядок нумерации уравнений Максвелла, вообще говоря, произволен.

Чаще всего первым уравнением системы уравнений Максвелла называют уравнение, которое

является обобщением на переменные поля эмпирического закона Ампера о возбуждении магнитного поля электрическими токами.

Максвелл высказал гипотезу, что магнитное поле порождается не только токами, текущими в проводниках (токи проводимости), но и переменными электрическими полями в диэлектриках или вакууме. Величина, пропорциональная скорости изменения электрического поля во времени, была названа Максвеллом током смещения. Ток смещения возбуждает магнитное поле по тому же закону, что и ток проводимости (позднее это было подтверждено экспериментально, А. А. Эйхенвальд, 1908). Полный ток, равный сумме тока проводимости и тока смещения, всегда является замкнутым.

  Первое уравнение Максвелла имеет вид:

.

то есть циркуляция вектора напряжённости магнитного поля вдоль замкнутого контура L (сумма скалярных произведений вектора Н в данной точке контура на бесконечно малый ориентированный отрезок dl контура) определяется полным током через произвольную поверхность S, ограниченную данным контуром. Здесь j_n — проекция плотности тока проводимости j на нормаль к бесконечно малой площадке ds, являющейся частью поверхности S, D_n/t — проекция плотности тока смещения на ту же нормаль.

Второе уравнение Максвелла является математической формулировкой закона электромагнитной индукции Фарадея-Максвелла и записывается в виде:

то есть циркуляция вектора напряжённости электрического поля вдоль замкнутого контура L (эдс индукции) определяется скоростью изменения потока вектора магнитной индукции через поверхность S, ограниченную данным контуром. Здесь B_n — проекция на нормаль к площадке ds вектора магнитной индукции В; знак минус соответствует правилу Ленца для направления индукционного тока.

  Третье уравнение Максвелла выражает опытные данные об отсутствии магнитных зарядов, аналогичных электрическим (магнитное поле порождается только токами):

,

то есть поток вектора магнитной индукции через произвольную замкнутую поверхность S равен нулю.

  Четвёртое уравнение (обычно называемое теоремой Гаусса) представляет собой обобщение закона взаимодействия неподвижных электрических зарядов - закона Кулона:

,

то есть поток вектора электрической индукции через произвольную замкнутую поверхность S определяется электрическим зарядом, находящимся внутри этой поверхности (в объёме V, ограниченном данной поверхностью).

Если считать, что векторы электромагнитного поля (Е, В, D, Н) являются непрерывными функциями координат, то, рассматривая циркуляцию векторов Н и Е по бесконечно малым контурам и потоки векторов B и D через поверхности, ограничивающие бесконечно малые объёмы, можно от интегральных соотношений перейти к системе дифференциальных уравнений, справедливых в каждой точке пространства, то есть получить дифференциальную форму уравнений Максвелла (обычно более удобную для решения различных задач):

H = j + Dt.

E = B/t.

B = 0.

D = .

Здесь  = rot и  = div — дифференциальные операторы ротор (вихрь) и дивергенция (расходимость), действующие на векторы Н, Е, B и D. 

Уравнения Максвелла в интегральной форме или дифференциальной не образуют полной замкнутой системы, позволяющей рассчитывать электромагнитные процессы при наличии материальной среды. Необходимо их дополнить соотношениями, связывающими векторы Е, Н,D,В и j, которые не являются независимыми. Связь между этими векторами определяется свойствами среды и её состоянием, причём D и j выражаются через Е, а B — через Н:

D = D(E), B = B(Н), j = j(E).

  Эти три уравнения называются уравнениями состояния, или материальными уравнениями; они описывают электромагнитные свойства среды и для каждой конкретной среды имеют определённую форму. В вакууме D  ₀Е и B  ₀Н. Совокупность уравнений поля (полевых уравнений) и уравнений состояния (материальных уравнений) образуют полную систему уравнений.

Макроскопические уравнения Максвелла описывают среду феноменологически, не рассматривая сложного механизма взаимодействия электромагнитного поля с заряженными частицами среды. Уравнения Максвелла могут быть получены из уравнений Лоренца-Максвелла

для микроскопических полей и определённых представлений о строении вещества путём усреднения микрополей по малым пространственно-временным интервалам. Таким способом получаются как полевые уравнения, так и конкретная форма уравнений состояния, причём вид уравнений поля не зависит от свойств среды.

Уравнения состояния в общем случае очень сложны, так как векторы D, B и j в данной точке пространства в данный момент времени могут зависеть от полей Е и Н во всех точках среды во все предшествующие моменты времени. В некоторых средах векторы D и B могут быть отличными от нуля при Е и H равных нулю (сегнетоэлектрики и ферромагнетики). Однако для большинства изотропных сред, вплоть до весьма значительных полей, уравнения состояния имеют простую линейную форму:

D = ₀E,  B = ₀H,  j = E + j_cт.

  Здесь (r) — диэлектрическая проницаемость, а (r) — магнитная проницаемость среды, характеризующие соответственно её электрические и магнитные свойства (для вакуума  =  = 1); величину (r) называют удельной электропроводностью; j_cт — плотность сторонних токов, то есть токов, поддерживаемых любыми силами, кроме сил электрического поля (например, магнитным полем, диффузией и т. д.). В феноменологической теории Максвелла макроскопические характеристики электромагнитных свойств среды ,  и  должны быть найдены экспериментально. В микроскопической теории Лоренца — Максвелла они могут быть рассчитаны.

Проницаемости  и  фактически определяют тот вклад в электромагнитное поле, который вносят так называемые связанные заряды, входящие в состав электрически нейтральных атомов и молекул вещества. Экспериментальное определение , ,  позволяет рассчитывать электромагнитное поле в среде, не решая трудную вспомогательную задачу о распределении связанных зарядов и соответствующих им токов в веществе. Плотность заряда  и плотность тока j в уравнениях Максвелла — это плотности свободных зарядов и токов, причём вспомогательные векторы Н и D вводятся так, чтобы циркуляция вектора Н определялась только движением свободных зарядов, а поток вектора D — плотностью распределения этих зарядов в пространстве.

Если электромагнитное поле рассматривается в двух граничащих средах, то на поверхности их раздела векторы поля могут претерпевать разрывы (скачки). Из полевых уравнений следуют для границы сред граничные условия:

nH₂  nH₁ = j_пов,

nE₂  nE₁ = 0,

nD₂  nD₁ = ,

nB₂  nB₁ = 0.

Здесь j_пов и  — плотности поверхностных тока и заряда,  и  — соответственно векторное и скалярное произведения векторов, n — единичный вектор нормали к поверхности раздела в направлении от первой среды ко второй (12), а индексы относятся к разным сторонам границы раздела.

Полевые уравнения линейны, уравнения же состояния могут быть и нелинейными. Обычно нелинейные эффекты обнаруживаются в достаточно сильных полях. В линейных средах справедлив принцип суперпозиции: при наложении полей они не оказывают влияния друг на друга.

Из уравнений Максвелла вытекает ряд законов сохранения. В частности, из первого и четвёртого уравнений можно получить соотношение (так называемое уравнение непрерывности):

представляющее собой закон сохранения электрического заряда: полный ток, протекающий за единицу времени через любую замкнутую поверхность S, равен изменению заряда внутри объёма V, ограниченного этой поверхностью. Если ток через поверхность отсутствует, то заряд в объёме остаётся неизменным.

Из уравнений Максвелла следует, что электромагнитное поле обладает энергией и импульсом. Плотность энергии w_em (энергия единицы объёма поля) равна:

w_em = ED/2 + HB/2.

Электромагнитная энергия может перемещаться в пространстве. Плотность потока энергии определяется так называемым вектором Пойнтинга

S = EH = w_emcn.

Направление вектора Пойнтинга перпендикулярно как Е, так и Н и совпадает с направлением распространения электромагнитной энергии, а его величина равна энергии, переносимой в единицу времени через единицу поверхности, перпендикулярной к вектору S.

Если не происходит превращений электромагнитной энергии в другие формы, то, согласно уравнениям Максвелла изменение энергии в некотором объёме за единицу времени равно потоку электромагнитной энергии через поверхность, ограничивающую этот объём. Если внутри объёма за счёт электромагнитной энергии выделяется тепло, то закон сохранения энергии записывается в форме:

где Q — количество теплоты, выделяемой в единицу времени.

В дифференциальной форме закон сохранения энергии принимает вид

.

Плотность импульса электромагнитного поля g (импульс единицы объёма поля) связана с плотностью потока энергии соотношением: g =S/c

Электромагнитное поле всегда обладает энергией, а поток энергии и электромагнитный импульс отличны от нуля лишь в случае, когда одновременно существуют и электрическое и магнитное поля (причём эти поля не параллельны друг другу).

Уравнения Максвелла приводят к фундаментальному выводу о конечности скорости распространения электромагнитных взаимодействий (равной с = 310¹⁰ см/сек). Это означает, что при изменении плотности заряда или тока в некоторой точке пространства порождаемое ими электромагнитное поле в точке наблюдения изменяется не в тот же момент времени, а спустя время  = R/c, где R — расстояние от элемента тока или заряда до точки наблюдения. Вследствие конечной скорости распространения электромагнитных взаимодействий возможно существование электромагнитных волн, частным случаем которых (как впервые показал Максвелл) являются световые волны.

Электромагнитные явления протекают одинаково во всех инерциальных системах отсчёта. то есть удовлетворяют принципу относительности. В соответствии с этим уравнения Максвелла не меняют своей формы при переходе от одной инерциальной системы отсчёта к другой (релятивистски инвариантны). Форма уравнений Максвелла остаётся неизменной при переходе к новой инерциальной системе отсчёта, если пространственные координаты и время, векторы поля Е, Н, В, D, плотность тока j и плотность заряда  изменяются в соответствии с преобразованиями Лоренца. Релятивистски инвариантная форма уравнений Максвелла подчёркивает тот факт, что электрическое и магнитное поля образуют единое целое.