
ЛР №3
.doc
Министерство общего и профессионального образования РФ

Государственный Санкт-Петербургский электротехнический университет «ЛЭТИ» имени Ульянова (Ленина)
Кафедра ТОЭ
Отчет по лабораторной работе № 3
(Исследование свободных процессов в электрических цепях)
Выполнили: Антонов В.В.
Красовский Р.А.
Группа: 3322
Факультет: КТИ
Кафедра: АПУ
Проверил: Морозов Д.А.
Санкт – Петербург
2005
Протокол наблюдений к лабораторной работе № 3 (Исследование свободных процессов в электрических цепях)
Выполнили: Антонов В.В.
Красовский Р.А.
Группа: 3322
Проверил: Морозов Д.А.
Цель работы
Изучение связи между видом свободного процесса в электрической цепи и расположением собственных частот (корней характеристического уравнения) на комплексной плоскости; приближенная оценка собственных частот и добротности RLC – контура по осциллограммам.
Приборы и принадлежности
Осциллограф, омметр, вольтметр, заготовки схем, соединительные провода.
Ход эксперимента
Генератор импульсов, расположенный на лабораторной плате, подключить к генератору синусоидальных сигналов (ГС). Установить на выходе ГС напряжение U = 7 – 10 В, частоту fc = 2 кГц (аналогичной будет частота импульсов, возбуждающих свободные колебания в исследуемых цепях).
-
Исследование свободных процессов в цепи первого порядка.

Собрать схему, показанную на Рис. 1, (C = 0,02 мкФ, R = 5 кОм). Снять осциллограмму напряжения на конденсаторе, зафиксировав на ней полный период повторения сигналов Tc = 1/fc = 0,5 мс , который определяет масштаб времени при обработке осциллограмм.
-
Исследование свободных процессов в цепи второго порядка.

Собрать схему, показанную на Рис. 2, (C = 0,02 мкФ, L = 25 мГн). Снять, фиксируя период Tc, осциллограммы напряжения на резисторе при значениях R1 = 0.5 кОм (колебательный режим) и R1 = 3 кОм (апериодический режим). Изменяя величину R1, снять осциллограмму критического режима (граничного между колебательным и апериодическим режимами) и записать величину полученного сопротивления R1кр.
Обработка результатов эксперимента
Расчет собственных частот цепи первого порядка
В паузах между импульсами тока цепь
находится в свободном режиме (т.к.
источник возбуждения тока отключен).
Свободный процесс имеет вид:
паузах между импульсами тока цепь
находится в свободном режиме (т.к.
источник возбуждения тока отключен).
Свободный процесс имеет вид:
![]() (экспоненциальный процесс). В линейных
цепях свободный процесс описывается
линейными дифференциальными уравнениями
и его вид определяется корнями
характеристического полинома (т.е.
собственными частотами цепи). При
возбуждении цепи источником тока
собственные частоты можно теоретически
рассчитать как нули входной проводимости.
Для цепи, представленной на Рис.
1, произведем
машинный расчет ее собственных частот:
(экспоненциальный процесс). В линейных
цепях свободный процесс описывается
линейными дифференциальными уравнениями
и его вид определяется корнями
характеристического полинома (т.е.
собственными частотами цепи). При
возбуждении цепи источником тока
собственные частоты можно теоретически
рассчитать как нули входной проводимости.
Для цепи, представленной на Рис.
1, произведем
машинный расчет ее собственных частот:
Постоянная времени
![]() определяется как
определяется как
![]() .
С другой стороны, постоянная времени
.
С другой стороны, постоянная времени
![]() есть x-координата точки пересечения
касательной к осциллограмме в начальной
точке с осью абсцисс. На Рис.
3 изображена
данная касательная, x-координата которой
составляет
есть x-координата точки пересечения
касательной к осциллограмме в начальной
точке с осью абсцисс. На Рис.
3 изображена
данная касательная, x-координата которой
составляет
![]() ,
откуда по формуле, указанной выше,
получаем:
,
откуда по формуле, указанной выше,
получаем:
![]()
Расчет собственных частот цепи второго порядка
Собственные частоты цепи второго порядка, как в случае цепи первого порядка, есть корни ее характеристического полинома.
Р ассмотрим
сначала случай, представленный на Рис.
6. Цепь
второго порядка в колебательном режиме.
Аналитическое выражение для данного
режима цепи:
ассмотрим
сначала случай, представленный на Рис.
6. Цепь
второго порядка в колебательном режиме.
Аналитическое выражение для данного
режима цепи:
![]() .
Приведем машинный расчет данного случая:
.
Приведем машинный расчет данного случая:
Значение постоянной затухания можно рассчитать по осциллограмме на Рис. 6:

Т еперь
рассмотрим случай, представленный на
Рис. 4.
Цепь второго порядка в апериодическом
режиме. Аналитическое выражение,
описывающее данный режим цепи второго
порядка:
еперь
рассмотрим случай, представленный на
Рис. 4.
Цепь второго порядка в апериодическом
режиме. Аналитическое выражение,
описывающее данный режим цепи второго
порядка:
![]() .
Приведем машинный расчет данного
случая:
.
Приведем машинный расчет данного
случая:
Д алее:
случай,
представленный на Рис.
5. Цепь
второго порядка в критическом режиме.
Аналитическое выражение для данного
режима:
алее:
случай,
представленный на Рис.
5. Цепь
второго порядка в критическом режиме.
Аналитическое выражение для данного
режима:
![]() Приведем
машинный расчет данного случая:
Приведем
машинный расчет данного случая:
Отыскать собственные частоты для критического режима можно лишь приближенно, выделив, как показано пунктиром на Рис. 5, отдельные составляющие процесса. Далее расчет аналогичен соответствующей оценке частот собственных колебаний для цепи первого порядка (см. выше.). Итак, окончательно получаем:
![]()
Расчет добротности цепи второго порядка
Добротность для
последовательного RLC
– контура:
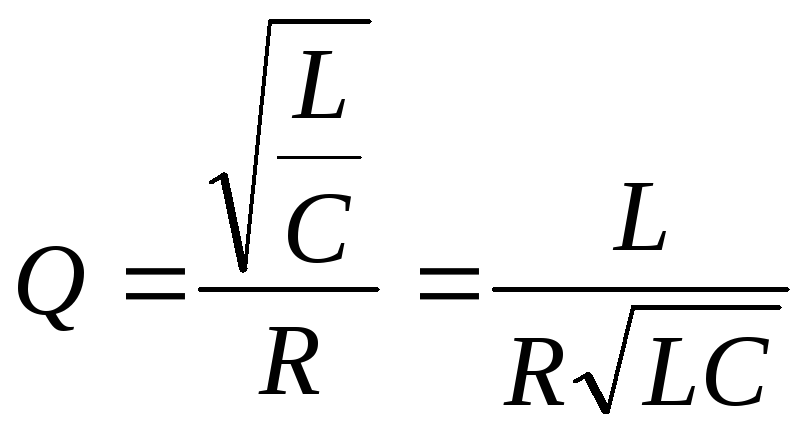 .
.

Численно получаем (R = 0.5 кОм):
![]() ,
значит, при данном сопротивлении в цепи
второго порядка должен быть колебательный
режим (что имеет место быть, судя по
форме полученной осциллограммы при
данном значении сопротивления).
,
значит, при данном сопротивлении в цепи
второго порядка должен быть колебательный
режим (что имеет место быть, судя по
форме полученной осциллограммы при
данном значении сопротивления).
Определим теперь
добротность по осциллограмме, изображенной
на Рис. 6:
![]() .
.
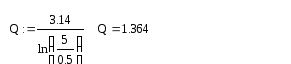
Численно получаем:
Заключение
-
При исследовании свободных процессов в цепях первого и второго порядка мы получили некоторые, порой, весьма значительные расхождения результатов теоретических расчетов с теми расчетами, которые были получены на основе данных проведенных экспериментов. Скорее всего, подобная ситуация возникла из-за большой погрешности при снятии показаний с осциллографа во время эксперимента; также свою отрицательную роль сыграли собственные погрешности используемых приборов, а также несовершенная конструкция других элементов цепи..
-
Мы убедились в том, что форма реакции цепи зависит от вида ее собственных частот: если собственные частоты вещественные — наблюдается апериодический режим, комплексно-сопряженные — колебательный режим, кратные — критический апериодический режим.
