Модуль 4

Практичне заняття 4

Симетричні многочлени.

Означення і елементарні властивості.

Основна теорема теорії симетричних многочленів

Література

1. Основна

1.1. Завало С. Т. та ін. Алгебра і теорія чисел, ч.2, К.: Вища школа, 1976.

2. Завало С. Т. та ін. Алгебра і теорія чисел. Практикум, ч.2, К.: Вища школа, 1986.

2. Додаткова

1. Окунєв Л. Я. Сборник задач по высшей алгебре, издательство «Просвещение». – М., 1964. – 184 с.

1.2. Винберг Э. Б. Алгебра многочленов. Учебное пособие для студентов заочников ІІІ – ІV курсов физико-математических факультетов педагогических институтов. – М., «Просвещение», 1980. – 176 с.

1.3. Курош А. С. Курс Высшей алгебры. М.: Наука, 1968. – 432 с..

1.4. Солодовников А.С., Родина М.А. Задачник-практикум по курсу высшей алгебры,М., «Просвещение», ч. IV, 1985;

Теоретичні матеріали

Симетричним многочленом над числовим полем прийнято називати такий многочлен від невідомих над , який не змінюється при будь-якій перестановці невідомих

Многочлени 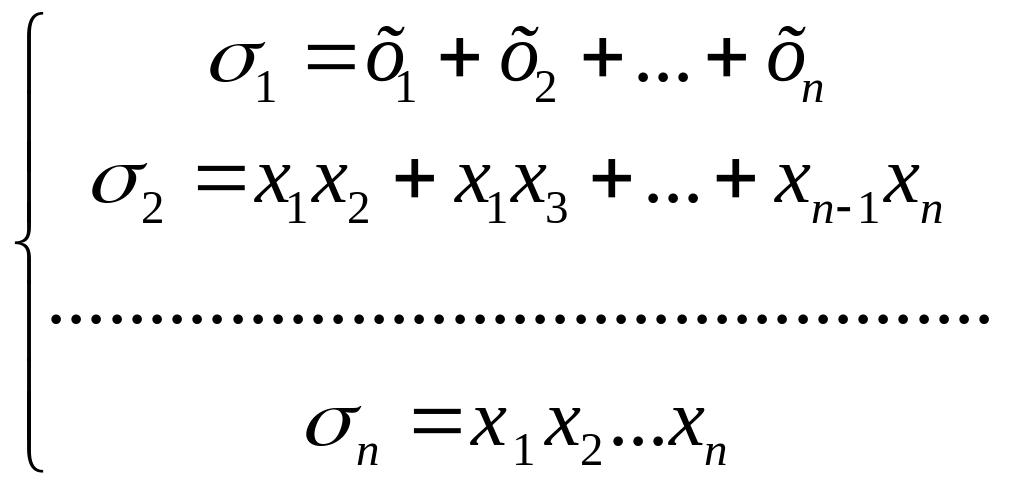називаються основними або елементарними симетричними многочленами від невідомих

Означення. Раціональний дріб від невідомих називається симетричним, якщо він залишається без зміни при будь-якій перестановці невідомих.

Так як за означенням симетричним многочленом над числовим полем прийнято називати такий многочлен від невідомих над , який не змінюється при будь-якій перестановці невідомих , то многочлен

є симетричним, легко переконатися, що він не змінюється при будь-якій перестановці невідомих:

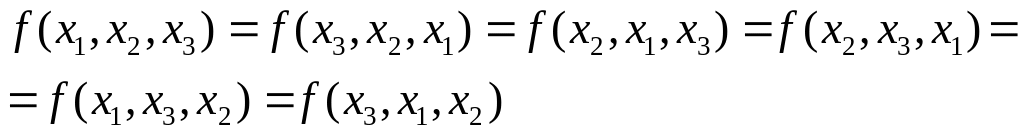
Візьмемо хоча б

Щоб отримати вираз треба у виразі (1) многочлена невідому замінити через , залишити без змін, а замінити на . Порівнюючи вирази (1) і (2) бачимо, що вони відрізняються один від одного лише порядком членів і порядком множників у кожному члені. Отже,

.

Вперше доводиться зіткнутися з симетричними многочленами при розв’язанні наступної задачі:

нехай дано рівняння -го степеня над полем

із старшим коефіцієнтом, який дорівнює 1. Виразити коефіцієнти рівняння через корені

Але ми уже знаємо, що коефіцієнти рівняння (3) повинні виражатися через корені по формулам Вієта, а саме:

Керуючись цими формулами, складемо тепер слідуючи многочлени від невідомих:

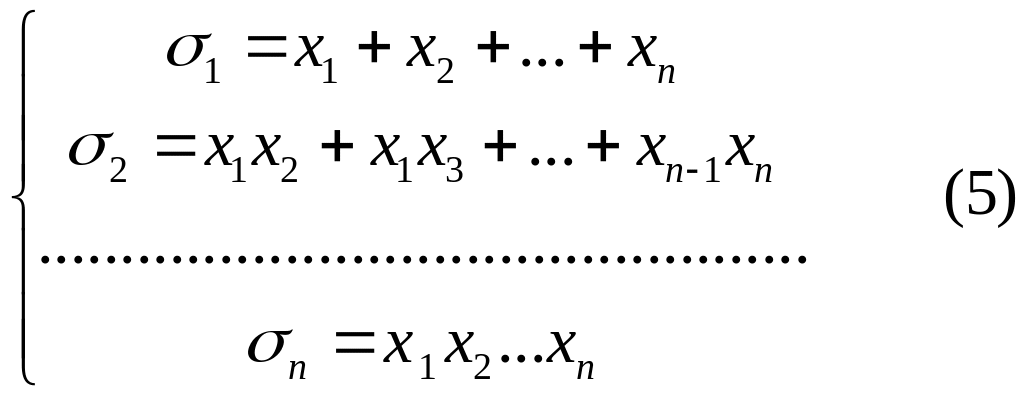
легко побачити, що многочлени (5) є симетричними. Справді, рівності (4), очевидно, не залежать від нумерації коренів Ми могли, наприклад, кореню приписати другий номер, хоча б 2, а кореню - номер, що дорівнює ; ця зміна нумерації не змінює рівність (4), так як при їх виведенні зовсім не важливо, який корінь потрібно позначити через , який – через і так далі.

Многочлени (5) називаються основними чи елементарними симетричними многочленами від невідомих

Із означення симетричного многочлена слідує, що якщо симетричний многочлен утримує член , то він утримує всі члени виду , які отримуються із даного будь-якими перестановками показників .

Не важко помітити, що сума, різниця і добуток двох симетричних многочленів над полем в свою чергу є симетричними многочленами над тим же полем .

Властивості довільних симетричних многочленів

1. Сума, різниця і добуток симетричних многочленів над деяким полем є знову симетричний многочлен над цим полем.

Наслідок. Множина всіх симетричних многочленів над полем утворює область цілісності з одиницею відносно дій додавання і множення.

2. Якщо симетричний многочлен містить деякий член (6), то він містить і член, утворений з (6) внаслідок будь-якої перестановки показників

Наслідок. Якщо (7) є вищий член симетричного многочлена, то