Модуль 3

Практичне заняття 4

Межі дійсних коренів. Число дійсних коренів.

Відокремлення дійсних коренів методом Штурма

Основні теоретичні відомості

Многочлени з дійсними коефіцієнтами будемо розглядати як дійсні неперервні функції дійсної змінної .

Розглянемо два способи знаходження границь коренів.

Перший спосіб. Неважко переконатися, що дійсні корені многочлена

потрібно шукати в інтервалі , де 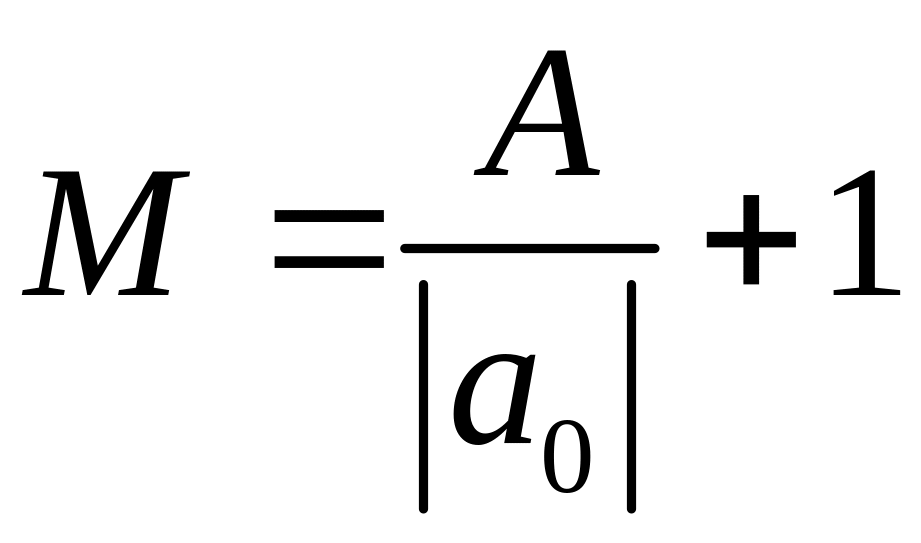, найбільша із абсолютних величин коефіцієнтів

Справді, величина є верхньою межею модулів комплексних коренів многочлена , а тому дійсні корені многочлена повинні лежати в інтервалі .

Другий спосіб (Спосіб Ньютона). Він має своєю основою наступне: якщо всі похідні многочлена го степеня додатні при , але , то існує таке число , що при буде додатній і сам многочлен разом із своїми похідними .

Легко бачити, що число , при якому многочлен і всі його похідні додатні, є верхнею межею додатних коренів многочлена.

Справді, при всі члени розкладу

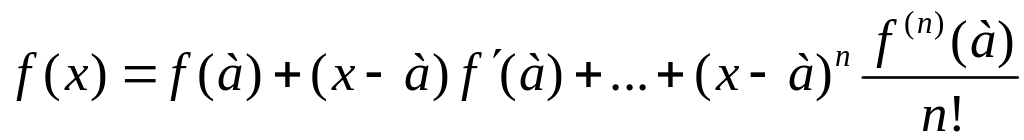
будуть, очевидно, додатні, в силу чого при . Тоді при многочлен не може перетворюватися в нуль і тому його дійсні корені повинні бути менші а.

Таким чином, ми приходимо до слідуючого способу визначення меж дійсних коренів многочлена .

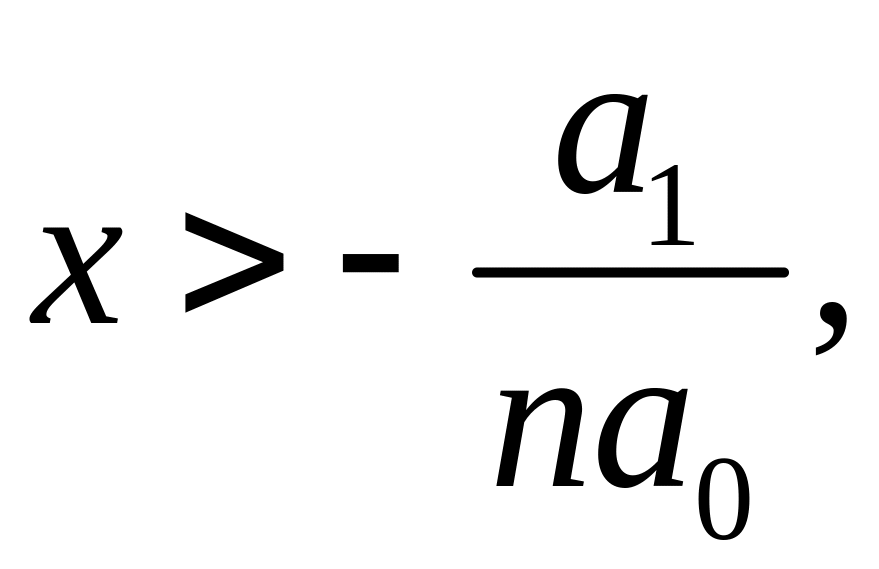Спосіб Ньютона. Старший коефіцієнт даного многочлена n-го степеня завжди можна зробити додатнім, потрібно тільки помножити на -1. Тому нехай Звертаємося до -ї похідної Якщо то Отже, можна підібрати таке додатне число щоб похідна при була додатною. При цьому -а похідна додатна при всіх значеннях , так як

Звідси можна підібрати таке , щоб при були додатними і . Оскільки і додатні при можна підібрати таке , щоб при були додатними і т. д. Вкінці ми доберемося до і знайдемо для нього верхню межу дійсних коренів.

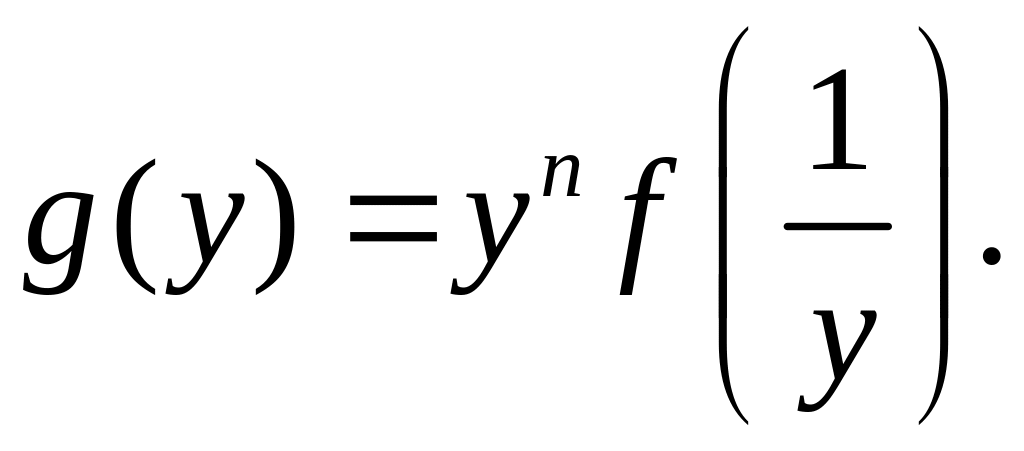Щоб знайти нижню границю дійних коренів , замінюємо через і розглядаємо многочлен Якщо верхня межа додатних коренів , то буде нижньою межею додатних коренів даного многочлена .

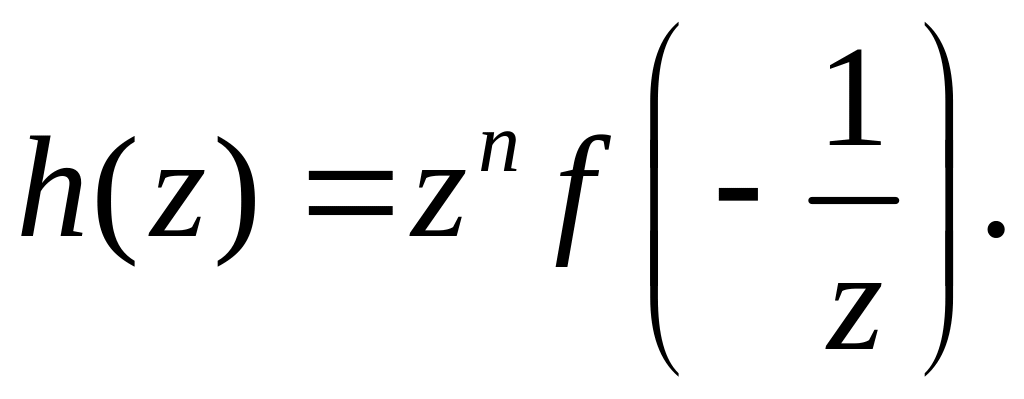Щоб знайти верхню межу від’ємних коренів , підставляємо і розглядаємо многочлен Якщо - верхня межа додатних коренів , то буде верхньою межею від’ємних коренів .

Щоб знайти нижню межу від’ємних коренів , підставляємо і розглядаємо многочлен Якщо верхня межа додатних коренів , то буде нижньою межею від’ємних коренів .

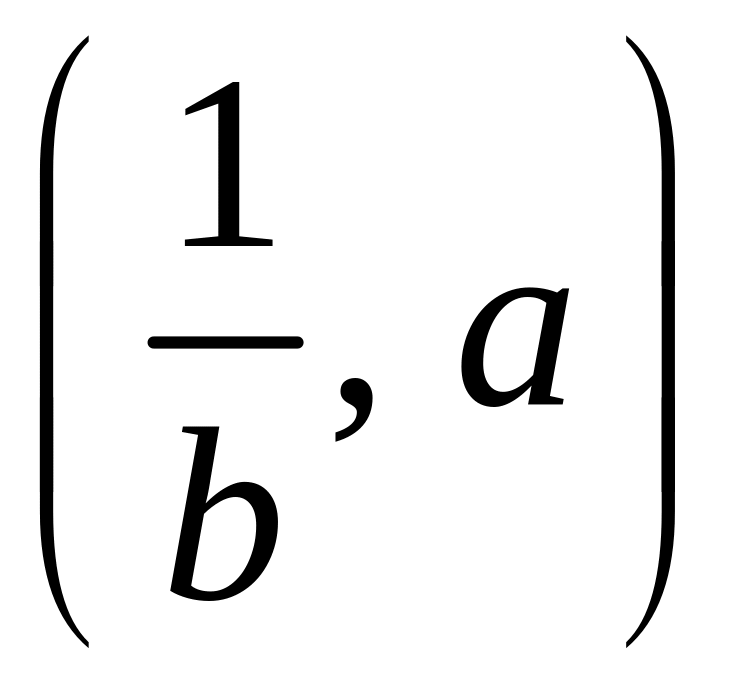Таким чином, всі додатні корені многочлена потрібно шукати в інтервалі , а всі від’ємні корені – в інтервалі

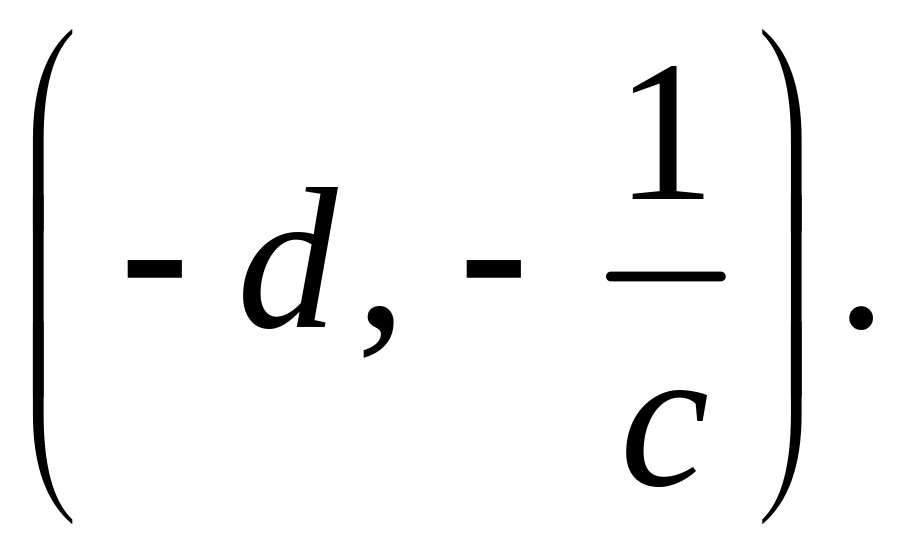
Число дійсних коренів

Число дійсних коренів з урахуванням кратності або дорівнює степеню рівняння, або на парне число менше. Будь-яке рівняння непарного степеня з дійсними коефіцієнтами має хоча б один дійсний корінь.

Обчислюючи значення многочлена в окремих точках, ми можемо знайти, що в деяких точках він приймає значення різних знаків. Оскільки многочлен – неперервна функція, звідси випливає, що в деякій точці інтервалу він повинен перетворюватися в нуль. (Звісно, це ще не означає, що в інтервалі знаходиться рівно один корінь многочлена ) .

Таким способом ми можемо оцінити знизу число дійсних коренів. Однак точне визначення цього числа потребує залучення інших методів.

Існують теореми, наприклад, теорема Штурма, які дозволяють точно визначити число дійсних коренів будь-якого многочлена з дійсними коефіцієнтами.