
- •19. Выражение тока, напряжения э.Д.С. Комплексными числами. Закон Ома в комплексной орме. Сопротивление и проводимость – в комплексной форме.
- •20. Законы Киргофа в комплексной форме. Выражение мощности в Комплекс форм
- •23. Колебательный контур. Энергетические процессы
- •24.Трехфазная система переменного тока, её определение. Принцип получения трех фазной э.Д.С.Волновые и Векторные Диаграмы.
- •25.Трехфазная система переменного тока, соедененая в в звезду.Фазы и ленейные напряжения , связь между нимиВолновые и вектроные диаграммы
- •26.Расчет Трех фазная система переменного тока при соедененая в звезду. . Нулевой провод
- •27. Трехфазная система переменного тока, соединенного в треугольник. Фазные и ленейные токи связь между ними Волновые и векторные диаграммы
15. Расчет разветвленных цепей переменного тока методом проводимости.
Определяем
полное сопротивление ветвей: z=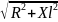
Определяем
активные проводимости в ветвях и цепи:
g=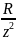 ;
;
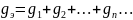
Определяем
реактивную проводимость ветвей и цепи:
bl=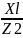 ;
bc=
;
bc=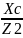 ;
;
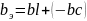
Определяем
полную проводимость: y=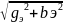
Любым возможным способом определяем входное напряжение и определяем входной ток
Iвх=Uвх*y.
Определяем мощности:
Активная:
P=U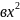 *g
*g
Реактивная:
Q=
U
*
Полная: S= U *y
16. Коэфициэнт мощности, его экономическое значение
1.Коэффициент мощности — безразмерная физическая величина, являющаяся энергетической характеристикой электрического тока. Коэффициент мощности характеризует приёмник электроэнергии переменного тока, а именно — степень линейности нагрузки. Равен отношению потребляемой электроприёмником активной мощности к полной мощности. Активная мощность расходуется на совершение работы. Полная мощность — геометрическая сумма активной и реактивной мощностей (в случае синусоидальных тока и напряжения). В общем случае полную мощность можно определить как произведение действующих (среднеквадратических) значений тока и напряжения в цепи. Полная мощность равна корню квадратному из суммы квадратов активной и неактивной мощностей. В качестве единицы измерения полной мощности принято использовать вольт-ампер (В∙А) вместо ватта (Вт).
В электроэнергетике для коэффициента мощности приняты обозначения cos φ (где φ — сдвиг фаз между силой тока и напряжением) либо λ. Когда для обозначения коэффициента мощности используется λ, его величину обычно выражают в процентах.
При наличии реактивной составляющей в нагрузке кроме значения коэффициента мощности иногда также указывают характер нагрузки: активно-ёмкостный или активно-индуктивный. В этом случае коэффициент мощности соответственно называют опережающим или отстающим.
2. Способы увеличения «косинуса фи». Вышеперечисленные последствия низкого cos с достаточной убедительностью говорят о том, что необходимо вести борьбу за высокий cos . К мерам увеличения соs относятся:1. Правильный выбор типа, мощности и скорости вновь устанавливаемых двигателей.2. Увеличение загрузки двигателей.3. Недопущение работы двигателей вхолостую продолжительное время.4. Правильный и высококачественный ремонт двигателей.5. Применение статических (т. е. неподвижных, невращающнхся) конденсаторов
17. Расчет цепей переменного тока символическим методом
i=(йот)
10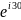 =10(cos30+isin30)=8.6+i5=
=10(cos30+isin30)=8.6+i5=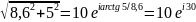 Действие
с комплексными числами и деление
производных в пкозательной форме
сложение и вычитание в алгебрагической:
Действие
с комплексными числами и деление
производных в пкозательной форме
сложение и вычитание в алгебрагической: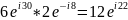 ;
6
;
6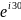 :2
:2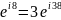 Выражение электрической техники
велечины с помощью компдексных чисел
активного сопротивления (R)
и активноё мощности (P)
выражение действительности числа
(1,2,3,4…), реактивное сопротивление (Xl),
(Xc)
и реактивная мощность(Ql),(Qc)выражены
мнимыми числами (i4-i20-i50…).
Выражение электрической техники
велечины с помощью компдексных чисел
активного сопротивления (R)
и активноё мощности (P)
выражение действительности числа
(1,2,3,4…), реактивное сопротивление (Xl),
(Xc)
и реактивная мощность(Ql),(Qc)выражены
мнимыми числами (i4-i20-i50…).
18.Формы записи комплексных чисел, связь между ними. Действия над комплексными числ
Ко́мпле́ксные[1] чи́сла, — расширение множества вещественных чисел, обычно обозначается . Любое комплексное число может быть представлено как формальная сумма x + iy, где x и y — вещественные числа, i — мнимая единица[2] Комплексное число z можно определить как упорядоченную пару вещественных чисел (x,y). Введём операции сложения и умножения таких пар следующим образом:Вещественные числа являются в этой модели подмножеством множества комплексных чисел и представлены парами вида , причём операции с такими парами согласованы с обычными сложением и умножением вещественных чисел. Ноль представляется парой единица — а мнимая единица — На множестве комплексных чисел ноль и единица обладают теми же свойствами, что и на множестве вещественных, а квадрат мнимой единицы, как легко проверить, равен , то есть − 1
Сравнение
a + bi = c + di означает, что a = c и b = d (два
комплексных числа равны между собой
тогда и только тогда, когда равны их
действительные и мнимые части).Сложение
(a
+ bi)
+ (c
+ di)
= (a
+ c)
+ (b
+ d)i.Вычитание
(a
+ bi)
− (c
+ di)
= (a
− c)
+ (b
− d)i.Умножение
(a+bi)*(c+di)=ac+bci+adi+bdi2=(ac-bd)+(bc+ad)I;Деление
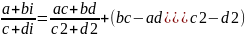
19. Выражение тока, напряжения э.Д.С. Комплексными числами. Закон Ома в комплексной орме. Сопротивление и проводимость – в комплексной форме.
 Каждому вектору
на комплексной плоскости соответствует
определенное комплексное число, которое
может быть записано в : показательной
Каждому вектору
на комплексной плоскости соответствует
определенное комплексное число, которое
может быть записано в : показательной
![]() ригонометрической
или
ригонометрической
или![]() алгебраической
алгебраической
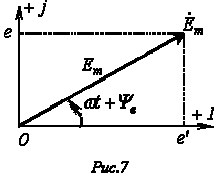
![]() - формах. Например, ЭДС
- формах. Например, ЭДС![]() изображенной на рис. 7 вращающимся
вектором, соответствует комплексное
число
изображенной на рис. 7 вращающимся
вектором, соответствует комплексное
число![]() Фазовый
угол
Фазовый
угол![]() определяется
по проекциям вектора на оси “+1” и “+j”
системы координат, как
определяется
по проекциям вектора на оси “+1” и “+j”
системы координат, как
![]() 2. Закон Ома записывается формулой:
2. Закон Ома записывается формулой:
![]() Где: I — сила тока (А), U — напряжение
(В), R — сопротивление (Ом).Следует иметь
в виду, что закон Ома является
фундаментальным (основным) и может быть
применён к любой физической системе,
в которой действуют потоки частиц или
полей, преодолевающие сопротивление.
Закон Ома в комплексной форме получаем
из формулы для комплексного сопротивления:
Где: I — сила тока (А), U — напряжение
(В), R — сопротивление (Ом).Следует иметь
в виду, что закон Ома является
фундаментальным (основным) и может быть
применён к любой физической системе,
в которой действуют потоки частиц или
полей, преодолевающие сопротивление.
Закон Ома в комплексной форме получаем
из формулы для комплексного сопротивления:
![]() 3. Комплексное сопротивление и комплексная
проводимость. Отношение комплексной
амплитуды напряжения на зажимах
двухполюсника к комплексной амплитуде
тока, протекающего через эти зажимы,
называется комплексным сопротивлением
пассивного двухпо-люсника
3. Комплексное сопротивление и комплексная
проводимость. Отношение комплексной
амплитуды напряжения на зажимах
двухполюсника к комплексной амплитуде
тока, протекающего через эти зажимы,
называется комплексным сопротивлением
пассивного двухпо-люсника
![]() Модуль комплексного сопротивления,
равный отношению амплитуды напряжения
к амплитуде тока называется полным
сопротивлением двухполюсника, т.е.
z=mod(Z)= Um/ Im ,Ом. Аргументом комплексной
проводимости является фазовый сдвиг
между напряжением и током на зажимах
двуполюсника, взятый со знаком (-).
Представляя комплексную проводимость,
как комплексное число, в алгебраической
форме,получим.Y=y
Cosj
-j
y
Sinj
=
Модуль комплексного сопротивления,
равный отношению амплитуды напряжения
к амплитуде тока называется полным
сопротивлением двухполюсника, т.е.
z=mod(Z)= Um/ Im ,Ом. Аргументом комплексной
проводимости является фазовый сдвиг
между напряжением и током на зажимах
двуполюсника, взятый со знаком (-).
Представляя комплексную проводимость,
как комплексное число, в алгебраической
форме,получим.Y=y
Cosj
-j
y
Sinj
=
![]() Вещественная и мнимая части комплексной
проводимости двухполюсника носят
название соответственно активной и
реактивной составляющих комплексной
проводимости.
Вещественная и мнимая части комплексной
проводимости двухполюсника носят
название соответственно активной и
реактивной составляющих комплексной
проводимости.
20. Законы Киргофа в комплексной форме. Выражение мощности в Комплекс форм
По
первому закону Кирхгофа, алгебраическая
сумма мгновенных значений токов,
сходящихся в любом узле схемы, равна
нулю:
![]() Равенство не нарушится, если вместо
токов подставить соответствующие
комплексы. Это и будет выражение для
первого закона Кирхгофа в комплексной
форме:
Равенство не нарушится, если вместо
токов подставить соответствующие
комплексы. Это и будет выражение для
первого закона Кирхгофа в комплексной
форме:
![]() где N
- количество ветвей, подходящих к узлу.По
второму закону Кирхгофа, в любом
(замкнутом) контуре справедливо равенство
алгебраических сумм мгновенных значений
напряжений на сопротивлениях контура
и ЭДС:
где N
- количество ветвей, подходящих к узлу.По
второму закону Кирхгофа, в любом
(замкнутом) контуре справедливо равенство
алгебраических сумм мгновенных значений
напряжений на сопротивлениях контура
и ЭДС:
![]() Заменив напряжения и ЭДС на
соответствующие комплексы, получим
выражение для второго закона Кирхгофа
в комплексной форме:
Заменив напряжения и ЭДС на
соответствующие комплексы, получим
выражение для второго закона Кирхгофа
в комплексной форме:
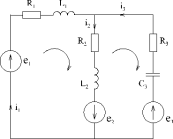
![]() где P
- количество элементов в контуре,M
- количество ЭДС в контуре.Пример:
где P
- количество элементов в контуре,M
- количество ЭДС в контуре.Пример:
![]()
2.
Комплексная мощность.Активную, реактивную
и полную мощности можно определить,
пользуясь комплексными изображениями
напряжения и тока. Пусть
![]()
![]() Тогда комплекс
полной мощности:
Тогда комплекс
полной мощности:
![]() где I-
комплекс, сопряженный с комплексом I.
где I-
комплекс, сопряженный с комплексом I.
![]()
Комплексной мощности можно поставить в соответствие треугольник мощностей (см. рис. 4). Рис. 4 соответствует (активно-индуктивная нагрузка), для которого имеем:
![]()
22.
Резонанс токов, его условие. Резонансные
кривые, частотные хар-ки, понятие
добротности, затухания, понятие о
добротности. Так как току с частотой f
оказывается значительное сопротивление,
то и падение напряжения на контуре при
частоте f будет максимальным. Это
свойство контура получило название
избирательность, оно используется в
радиоприемниках для выделения сигнала
конкретной радиостанции.Колебательный
контур, работающий в режиме резонанса
токов, является одним из основных узлов
электронных генераторов. Резонансными
кривыми называются зависимости тока
и напряжения от частоты. В качестве их
примера на рис. 3 приведены типовые
кривые I(f); и для цепи на рис. 1 при
U=const.Важной характеристикой резонансного
контура является добротность Q,
определяемая отношением напряжения
на индуктивном (емкостном) элементе к
входному напряжению:
![]() - и характеризующая “избирательные”
свойства резонансного контура, в
частности его полосу пропускания
- и характеризующая “избирательные”
свойства резонансного контура, в
частности его полосу пропускания
![]() Другим параметром резонансного контура
является характеристическое сопротивление,
связанное с добротностью соотношением
Другим параметром резонансного контура
является характеристическое сопротивление,
связанное с добротностью соотношением
![]() или с учетом (4) и (5) для можно записать:
или с учетом (4) и (5) для можно записать:
![]()
![]() Если подать на
вход системы с передаточной функцией
W(p) гармонический сигнал
Если подать на
вход системы с передаточной функцией
W(p) гармонический сигнал
![]() то после завершения переходного процесса
на выходе установится гармонические
колебания
то после завершения переходного процесса
на выходе установится гармонические
колебания
![]() с той же частотой , но иными амплитудой
и фазой, зависящими от частоты
возмущающего воздействия. Подставим
выражения для u(t) и y(t) в уравнение
динамики (aоpn + a1pn - 1 + a2pn - 2 + ... + an)y = (bоpm
+ b1pm-1 + ... + bm)u.. Добро́тность — характеристика
колебательной системы, определяющая
полосу резонанса и показывающая, во
сколько раз запасы энергии в системе
больше, чем потери энергии за один
период колебаний.
с той же частотой , но иными амплитудой
и фазой, зависящими от частоты
возмущающего воздействия. Подставим
выражения для u(t) и y(t) в уравнение
динамики (aоpn + a1pn - 1 + a2pn - 2 + ... + an)y = (bоpm
+ b1pm-1 + ... + bm)u.. Добро́тность — характеристика
колебательной системы, определяющая
полосу резонанса и показывающая, во
сколько раз запасы энергии в системе
больше, чем потери энергии за один
период колебаний.
Добротность
обратно пропорциональна скорости
затухания собственных колебаний в
системе. То есть, чем выше добротность
колебательной системы, тем меньше
потери энергии за каждый период и тем
медленнее затухают колебания. Общая
формула для добротности любой
колебательной системы:
![]() где:f — частота колебанийW — энергия,
запасённая в колебательной системеPd
— рассеиваемая мощность.
где:f — частота колебанийW — энергия,
запасённая в колебательной системеPd
— рассеиваемая мощность.
Декремент затухания - величина, обратная числу колебаний, по истечении которых амплитуда убывает в е раз. Например, если d = 0,01, то амплитуда уменьшится в е раз после 100 колебаний. Декремент затухания характеризует число периодов, в течение которых происходит затухание колебаний, а не время такого затухания. Полное время затухания определяется отношением Т/d.
