
- •Поняття про визначник. Властивості визначників.
- •Поняття про визначник іі порядку.
- •Визначник ііі порядку.
- •Визначник - го порядку.
- •Властивості визначників
- •Мінори та алгебраїчні доповнення елемента визначника.
- •Теорема Лапласа та її наслідки.
- •Поняття про матрицю. Види матриць.
- •Поняття про матрицю
- •Дії над матрицями
- •Властивості дій над матрицями
- •Обернена матриця.
- •Означення рангу матриці.
- •Елементарні перетворення матриць.
- •Обчислення рангу матриці.
- •Поняття лінійної залежності.
- •Теорема про ранг матриці.
- •Поняття про слар та її розв’язки.
- •Поняття про систему рівнянь та її розв’язки.
- •Сумісність слар. Теорема Кронекера-Капеллі.
- •Методи розв’язання слар
- •Правило Крамера розв’язуванння системи n рівнянь з n невідомими.
- •Матричний метод розв‘язування систем n лінійних рівнянь з n невідомими.
- •Метод Гауса.
- •Класифікація систем за кількістю розв’язків.
Дії над матрицями
Сумою
(різницею)
двох матриць
і
![]() називається матриця
називається матриця
![]() ,
елементи якої рівні сумі (різниці)
відповідних елементів матриць
і
,
тобто
,
елементи якої рівні сумі (різниці)
відповідних елементів матриць
і
,
тобто
![]() (
(![]() ).
).
Добутком
матриці
на довільне число
![]() називається матриця, елементами якої
є добутки елементів матриці
на
називається матриця, елементами якої
є добутки елементів матриці
на
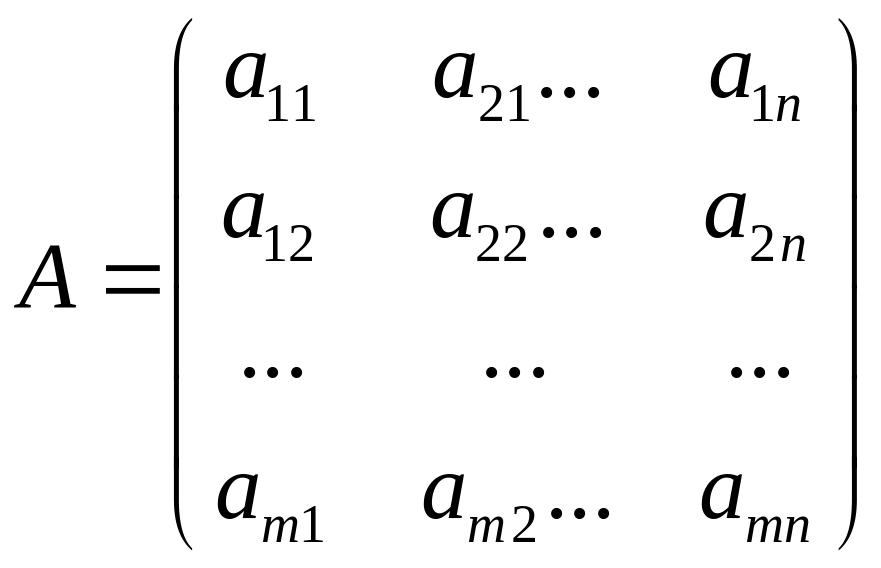 ;
; 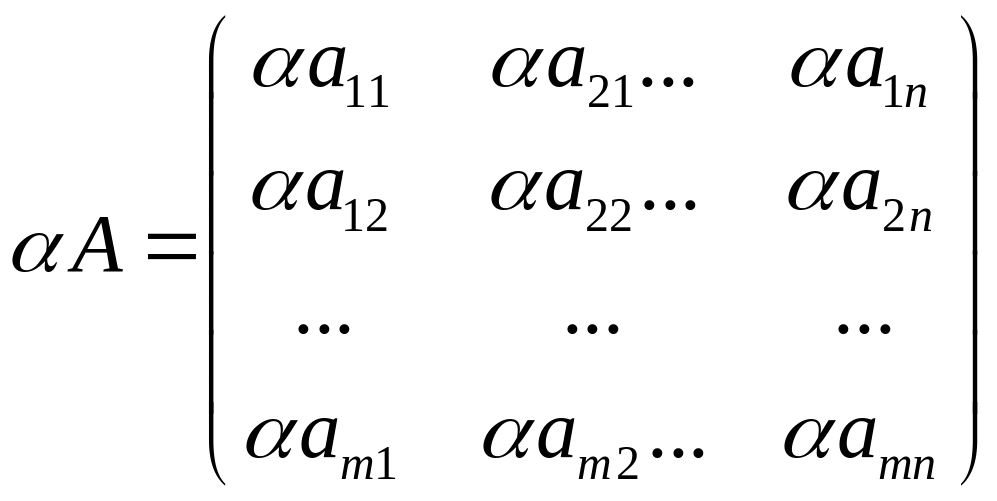
Добутком
mp-матриці
на pn-матрицю
називається
![]() -матриця
,
елементи якої
-матриця
,
елементи якої
![]() дорівнюють сумі добутків відповідних
елементів
дорівнюють сумі добутків відповідних
елементів
![]() -го
рядка матриці
і
-го
рядка матриці
і
![]() -го
стовпця матриці
,
тобто:
-го
стовпця матриці
,
тобто:
![]()
Добуток
матриці
на матрицю
позначається
![]() .
Добуток
має зміст лише за умови, що кількість
стовпців матриці
дорівнює числу рядків матриці
.
Добуток
має зміст лише за умови, що кількість
стовпців матриці
дорівнює числу рядків матриці
Приклад.
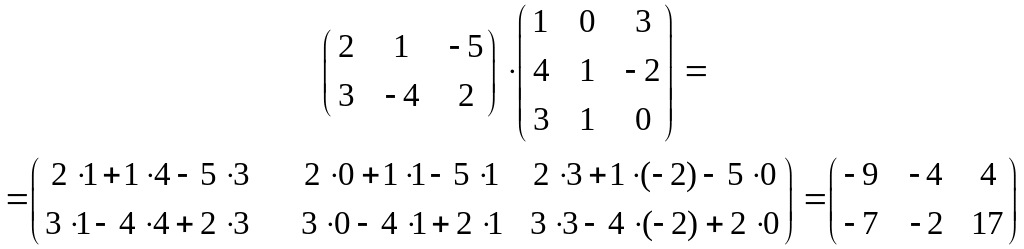
Властивості дій над матрицями
Добуток будь-якої матриці на одиничну матрицю відповідно порядку, як справа так і зліва, співпадає з матрицею , тобто:
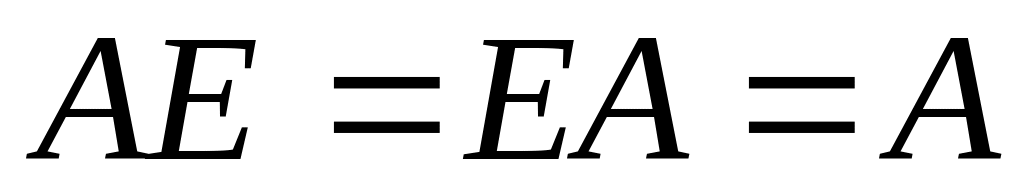
Одинична матриця примноженні матриць відіграє ту ж роль що і одиниця при множенні чисел.
Добуток матриці на нуль-матрицю є нуль-матрицею.
Множення матриць не підлягає комутативному закону.
Матриці, які підлягають комутативному закону, називаються комутативними.
Добуток матриць підлягає асоціативному (сполучному) закону:
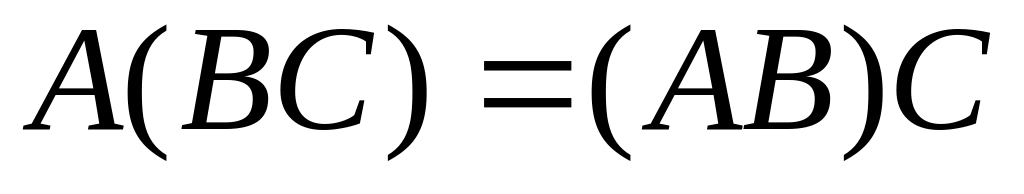
При множенні матриць виконується дистрибутивний закон:
![]()
Визначник добутку двох квадратних матриць дорівнює добутку їх визначників. Якщо
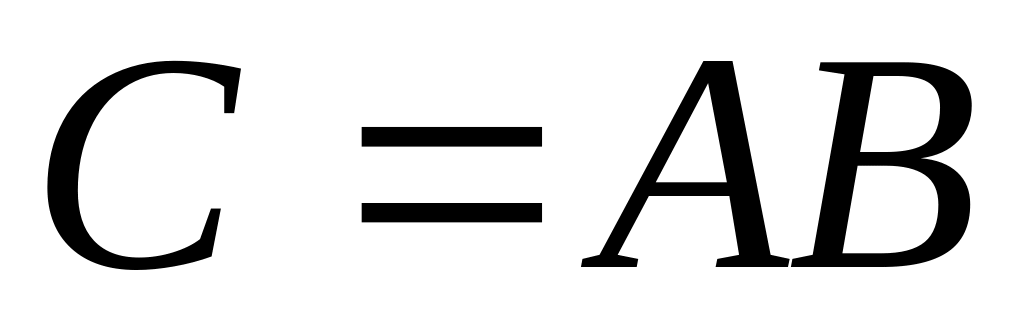 ,
то
,
то

Обернена матриця.
Означення.
Оберненою до даної квадратної матриці
називається
така
матриця
![]() ,
добуток
на
яку матриці
справа
є
одиничною
матрицею:
,
добуток
на
яку матриці
справа
є
одиничною
матрицею:
![]()
Теорема. Для кожної неособливої квадратної матриці існує обернена, притому тільки одна. Для особливої квадратної матриці обернена не існує.
Робоча формула для обчислення матриці , оберненої для матриці , має вигляд:
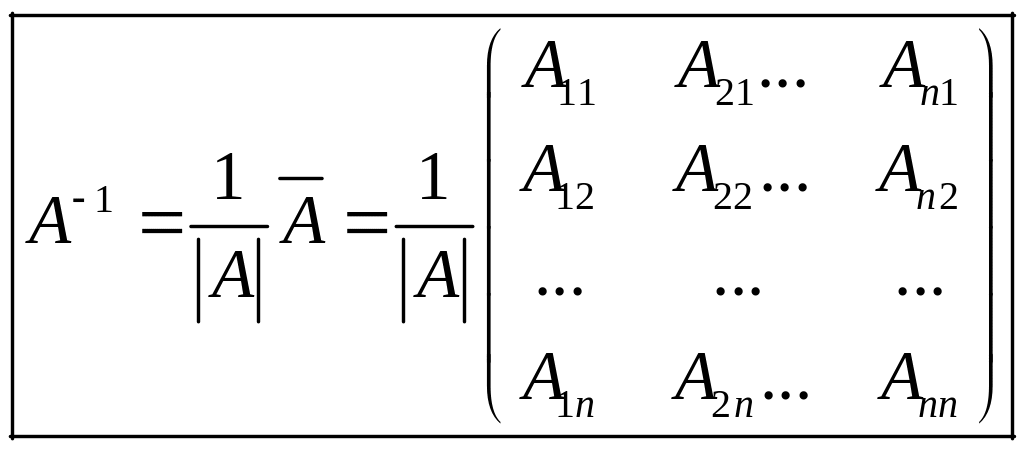
Означення рангу матриці.
Розглянемо прямокутну матрицю А, яка складається з т рядків та п стовпців:
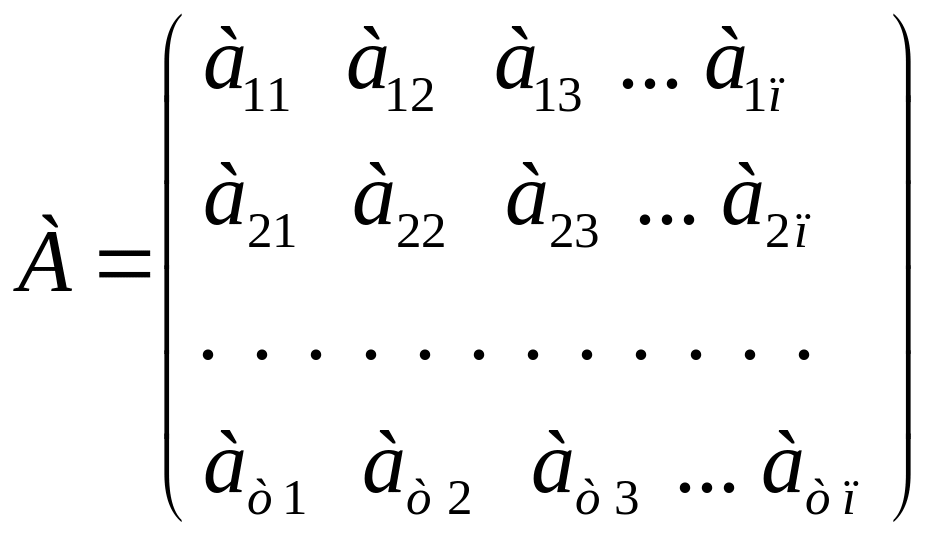 .
.
Нехай
![]() і
і
![]() .
Виділимо в цій матриці
.
Виділимо в цій матриці
![]() рядків і
стовпців. Із елементів, що стоять на
перетині виділених рядків і стовпців,
складtмо визначник
-го
порядку. Будь-який подібний визначник
називається мінором
матриці
А.
рядків і
стовпців. Із елементів, що стоять на
перетині виділених рядків і стовпців,
складtмо визначник
-го
порядку. Будь-який подібний визначник
називається мінором
матриці
А.
Означення. Рангом матриці А називається найвищий порядок відмінного від нуля мінора цієї матриці.
Якщо
ранг матриці
![]() ,
то серед мінорів цієї матриці є принаймні
один мінор
-го
порядку, відмінний від нуля. В той же
час всі мінори
,
то серед мінорів цієї матриці є принаймні
один мінор
-го
порядку, відмінний від нуля. В той же
час всі мінори
![]() -го
і вищих порядків дорівнюють нулеві.
Позначають ранг матриці
-го
і вищих порядків дорівнюють нулеві.
Позначають ранг матриці
![]() через
через
![]() .
Для обчислення рангу матриці її спочатку
спрощують за допомогою елементарних
перетворень.
.
Для обчислення рангу матриці її спочатку
спрощують за допомогою елементарних
перетворень.
Елементарні перетворення матриць.
До
елементарних
перетворень
матриці відносять: транспонування;
перестановку двох рядків (стовпців);
множення всіх елементів рядка (стовпця)
на довільне число
![]() ;
додавання до всіх елементів рядка
(стовпця) відповідних елементів
паралельного рядка (стовпця), помножених
на одне і те ж число.
;
додавання до всіх елементів рядка
(стовпця) відповідних елементів
паралельного рядка (стовпця), помножених
на одне і те ж число.
Теорема 1. (про елементарні перетворення). При елементарних перетвореннях матриці її ранг не змінюється.
Обчислення рангу матриці.
За допомогою елементарних перетворень будь-яку матрицю можна звести до матриці виду:
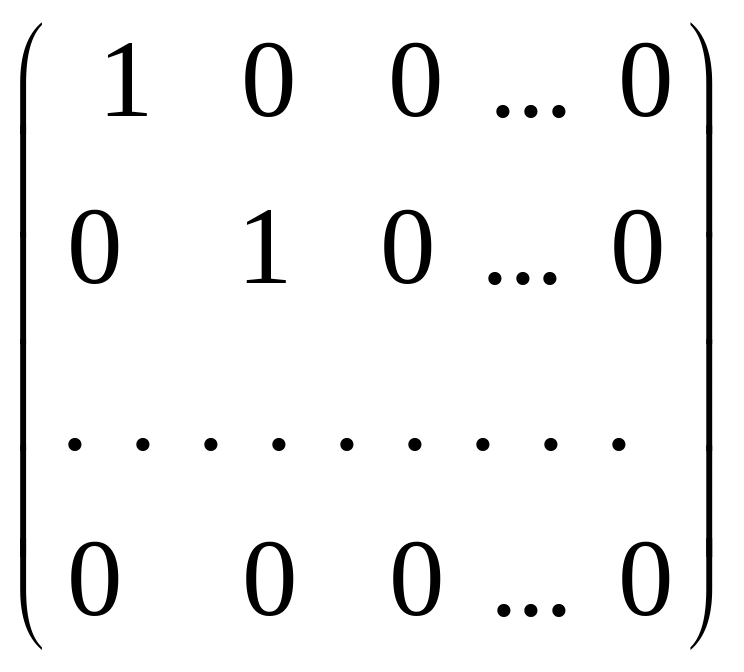 ,
,
де на головній діагоналі стоять одиниць а всі інші елементи дорівнюють нулю. Ранг одержаної, а отже, і даної матриць дорівнює .
Приклад. За допомогою елементарних перетворень обчислити ранг матриці:
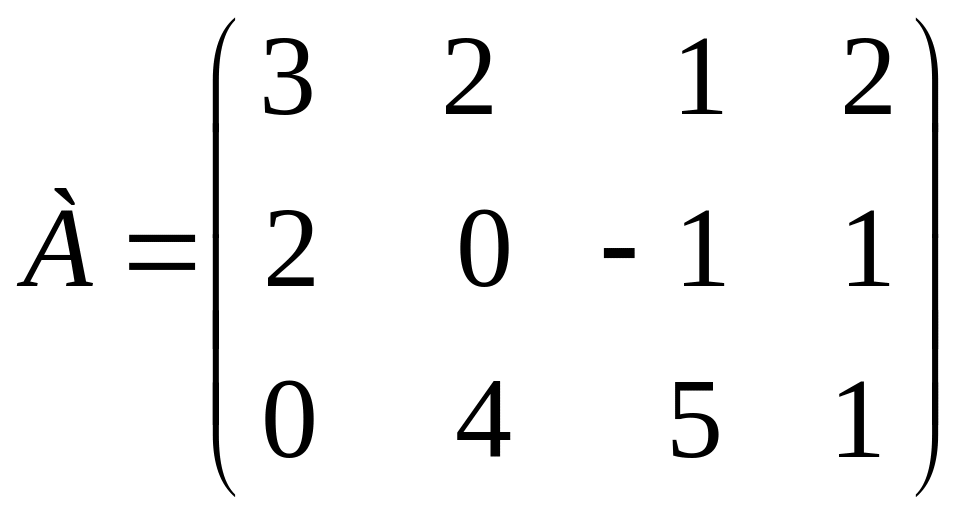
Розв’язання. Віднімаючи від ІІІ рядка подвоєний І і додаючи потроєний ІІ, одержимо:
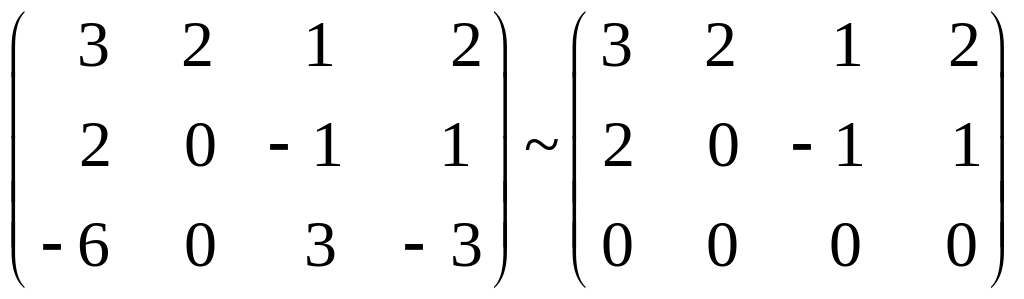
Віднімаючи ІV стовпчик від I, II від IV, маємо:
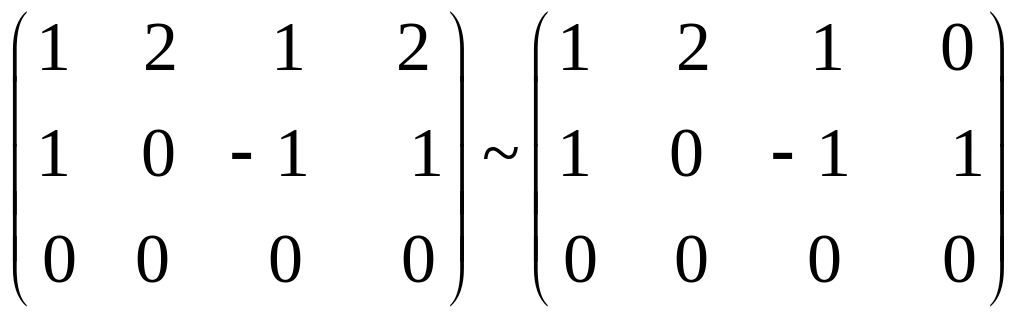
Віднімаючи ІV стовпчик від I, скорочуючи II на 2 і віднімаючи від III, маємо:
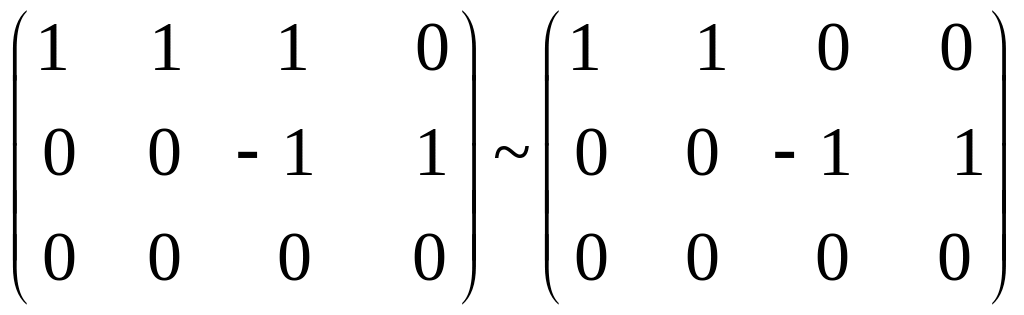
Віднявши I від II, додавши ІV до III і помінявши місцями II і ІV стовпчик, маємо:
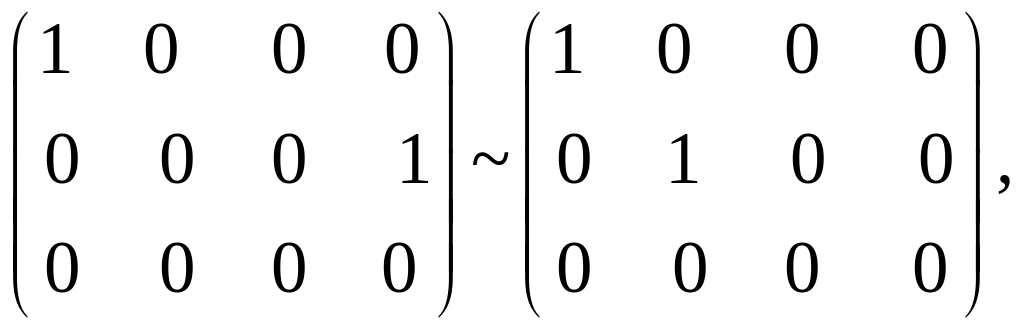
![]()
