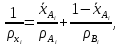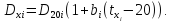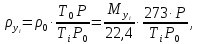4.1.2 Определение флегмового числа. Уравнения рабочей линии

Уравнения рабочих линий процесса связывают действительные концентрации компонента в жидкой и паровой фазах в любом сечении колонны.

а) Уравнение рабочей линии верхней части колонны:

((6)

б) Уравнение рабочей линии нижней части колонны:

(7)

где 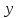– молярная доля легколетучего компонента в паре, входящем снизу на тарелку, (мол.);

– флегмовое число;

– число питания;

– молярная доля легколетучего компонента в жидкости, стекающей с этой тарелки, (масс.).

Число питания определяется по уравнению:

((8)

Определим число питания:

(

Рабочее число флегмы:

(9)

где – минимальное число флегмы.

Определяем минимальное число флегмы по уравнению:

(10)

Где - равновесная концентрация.

По уравнению (10) и рисунку А.2 определим минимальное число флегмы при условии, что графически было определенно, что

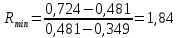
По уравнению (9) определим рабочее число флегмы:

Уравнение верхней рабочей линии (6) примет вид:

Уравнение нижней рабочей линии (7) примет вид:

4.1.3 Определение средних физических величин потоков пара и жидкости

Для определения основных размеров колонны, расходов греющего пара и воды требуется найти средние мольные, массовые составы, мольные, массовые и объёмные расходы по жидкости и пару, в также некоторые физические величины.

Для простой полной колонны, обогреваемой глухим паром (горячей водой) или острым паром, средние составы и расходы по жидкости и пару, а также физические величины определяют отдельно для верхней и нижней частей колонны.

А) Для жидкой фазы в верхней и нижней частях колонны

Мольные составы и определяют как среднеарифметические:

	(11)
	(12)

Где А – легколетучий компонент.

Мольные составы по уравнению (11) и (12) соответственно:

Мольные массы и определяются по уравнению (1):

Массовые составы и определяют по уравнению (2):

Средние температуры и определяем по Приложению А при соответствующих значениях и .

Плотности , 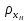определяю по уравнению:

(13)

где и – плотности легколетучего и труднолетучего компонентов при соответствующих температурах, .

Плотности легколетучего и труднолетучего компонентов при соответствующих температурах по [1] занесены в таблицу 3.

Таблица 3 - Плотность компонентов в зависимости от температуры

Компонент	Плотность,
Бензол	822	817
Хлороформ	1389,6	1383

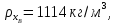
Рассчитываем динамические коэффициенты вязкости , :

(14)

где , – коэффициенты динамической вязкости легколетучего и труднолетучего компонентов.

Коэффициенты динамической вязкости легколетучего и труднолетучего компонентов при соответствующих температурах по [4] занесены в таблицу 4.

Таблица 4 – Динамические коэффициенты вязкости

Компонент	Коэффициент динамической вязкости,
Бензол	0,34001	0,325
Хлороформ	0,349	0,336

Рассчитаем динамические коэффициенты вязкости по уравнению (14):

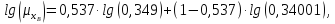
Рассчитаем температурный коэффициент:

(15)

где – динамический коэффициент вязкости жидкости при ;

– плотность жидкости при .

Из уравнения (15):

Таблица 5 – Коэффициенты вязкости и плотности жидкостей при [4]

Жидкость	Коэффициент вязкости,	Плотность жидкости,
Бензол	0,649	879
Хлороформ	0,57	1489
Вверху колонны
Внизу колонны

Коэффициент диффузии (при ):

(16)

где 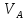и – мольные объёмы растворенного вещества и растворителя, ;

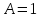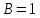и – коэффициенты, зависящие от свойств растворенного вещества и растворителя.

Мольные объёмы растворённого вещества [3]:

Используя уравнение (16):

Коэффициент диффузии:

(17)

Рассчитаем коэффициент диффузии по уравнению (17):

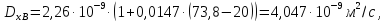
Поверхностные натяжения можно найти:

(18)

где 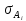и – поверхностные натяжения исходных веществ при соответствующих температурах, .

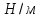По [4] поверхностные натяжения исходных веществ: ; ; ; .

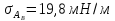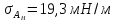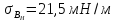Поверхностные натяжения по уравнению (18):

Массовые расходы:

	(19)
	(20)

где , – массовые расходы питания и дистиллята, .

Используя уравнения (19) и (20):

Объёмные расходы:

(21)

Используя уравнения (21):

Б) Для паровой фазы в верхней и нижней частях колонны

Мольные составы определяем по уравнениям рабочих линий (6) и (7):

Мольные массы определяем на основе уравнения (1):

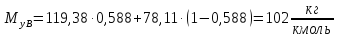
Массовые составы определяем на основе уравнения (2):

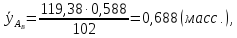
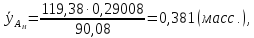
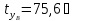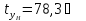Средние температуры и определим по Приложению А при соответствующих значениях и . (мольные)

Плотности смесей определим по уравнению Клапейрона:

(22)

где – плотность пара при нормальных условиях (, ), кг/м³

– средняя температура пара, К;

– среднее давление в колонне.

Динамические коэффициенты вязкости рассчитаем по приближённой формуле:

(23)

где , – коэффициенты динамической вязкости легколетучего и труднолетучего компонентов при соответствующих температурах.

Используя уравнение (23):

Коэффициент диффузии:

(24)

По уравнению (24):

Массовые расходы:

(25)

Объёмные расходы пара:

(26)