
2ЛБ
.docx
Министерство высшего образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ» (ТУСУР)
Кафедра комплексной информационной безопасности электронно-вычислительных систем (КИБЭВС)
РАБОТА С ГРАФАМИ
Отчет по лабораторной работе №2
по дисциплине «Технологии и методы программирования»
Студентка гр.737-1
______ Агеева В.С
Принял
Руководитель
_____Калмыков М.О.
Томск 2019
1 Введение
В ходе выполнения данной лабораторной работы необходимо для данного взвешенного ориентированного графа G без дуг отрицательного веса найти:
1. Кратчайшие пути от некоторой вершины a графа G до всех остальных вершин этого графа;
2. Контур минимальной длины (цикл, проходящий через каждую вершину ровно один раз и имеющий минимальный вес).
2 Ход работы
2.1 Выбор алгоритмов
Для быстроты и легкости обращения к ребрам граф был представлен в виде двумерного массива формата arr[i][j], а также произведения арифметических и логических действий с этим элементом.
Для выполнения первого задания был выбран алгоритм Дейкстра, данный алгоритм был выбран, потому что легок в реализации и имеет лучшую алгоритмическую сложность, нежели другие алгоритмы.
Для выполнения второго задания был выбран алгоритм прима, данный алгоритм был выбран, потому что его достоинство в том, что он обладает свойством определенности за конечное число итераций.
2.2 Описание алгоритмов
1) Для поиска кратчайшего пути от выбранной пользователем вершины до остальных был использован алгоритм Дейкстры. Каждой вершине графа сопоставляется метка — минимальное известное расстояние от этой вершины до D (другой). В результате пошаговой работы алгоритма на каждом шаге происходит посещение одной вершины и попытка уменьшить метку. После посещения всех вершин работа алгоритма завершается.
Метка самой вершины считается равной 0, а других вершин равными бесконечности, так как расстояния до других вершин неизвестны. Все вершины графа помечены как непосещенные.
Рассмотрим шаг алгоритма. В случае посещения всех вершин происходит завершение работы алгоритма. Иначе из ещё не посещённых вершин выбирается вершина u, имеющая минимальную метку. Ввиду особенности работы алгоритма мы рассматриваем все возможные маршруты, в которых u является предпоследним пунктом. Вершины, в которые ведут ребра из u, назовем соседними вершинами. Для каждой соседней вершины u, кроме отмеченных как посещенные, рассматривается новая длина пути, равная сумме значений текущей метки u и длины ребра, соединяющего u с этой соседней вершиной. Если полученное значение длины меньше значения метки соседней вершины, то происходит замена значения метки новым полученным значением. После рассмотрения всех соседних вершин, помечаем вершину u как посещенную и повторяем шаг алгоритма в случае непосещения всех вершин. Блок-схема алгоритма представлена на рисунке 2.1.
2) Для поиска контура минимальной длины был использован алгоритм прима. Искомый минимальный остов строится постепенно, добавлением в него рёбер по одному. Изначально остов полагается состоящим из единственной вершины (её можно выбрать произвольно). Затем выбирается ребро минимального веса, исходящее из этой вершины, и добавляется в минимальный остов. После этого остов содержит уже две вершины, и теперь ищется и добавляется ребро минимального веса, имеющее один конец в одной из двух выбранных вершин, а другой — наоборот, во всех остальных, кроме этих двух. И так далее, т.е. всякий раз ищется минимальное по весу ребро, один конец которого — уже взятая в остов вершина, а другой конец — ещё не взятая, и это ребро добавляется в остов (если таких рёбер несколько, можно взять любое). Этот процесс повторяется до тех пор, пока остов не станет содержать все вершины.
В итоге будет построен остов, являющийся минимальным. Если граф был изначально не связен, то остов найден не будет.
Блок-схема алгоритма представлена на рисунке 2.2.
2.3 Блок-схемы
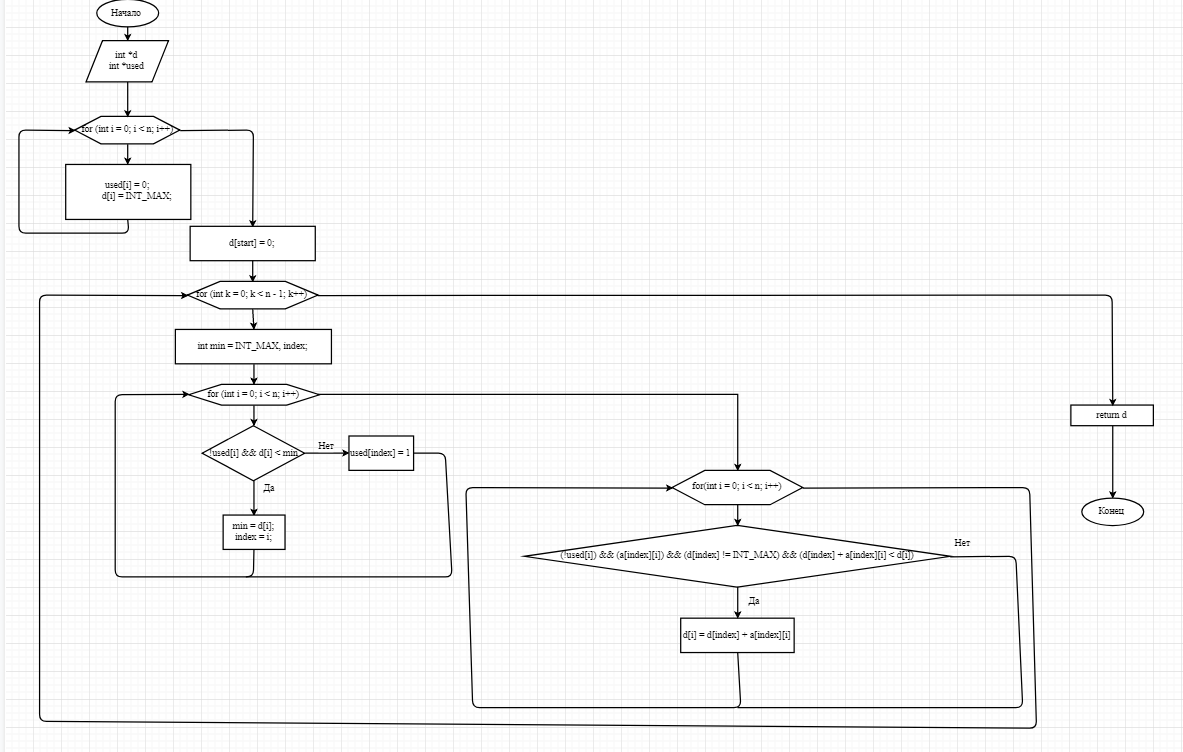
Рисунок 2.1 – Блок схема для функции нахождения кратчайшего пути

Рисунок 2.2 – Блок-схема для функции нахождения контура минимальной длины
2.4 Описание формата входных данных
Пользователь вводит количество вершин, квадратную матрицу и с какой вершины начинаем выполнять алгоритм.
2.5 Описание формата выходных данных
На вывод поступают данные о матрице смежности, расстояниях до вершин и длине контура минимальной длины. Соответственно для этих данных используются тип данных Int, допустимый диапазон [0; 100000] и тип данных String.
2.6 Описание тестовых данных
Граф для нахождения кратчайшего пути G1(V,E), где V – множество вершин, а E – множество ребер, представлен на рисунке 2.3.
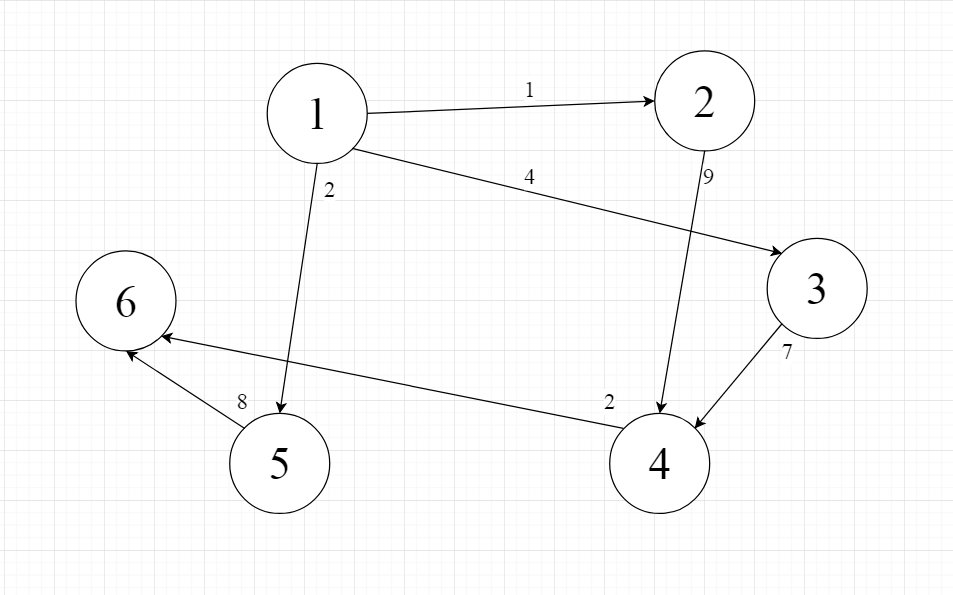
Рисунок 2.3 – Граф для первого задания
Матрица смежности графа G1 приведена в таблице 2.1.
Таблица 2.1 - Матрица смежности
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
0 |
1 |
4 |
0 |
2 |
0 |
|
2 |
0 |
0 |
0 |
9 |
0 |
0 |
|
3 |
4 |
0 |
0 |
7 |
0 |
0 |
|
4 |
0 |
9 |
7 |
0 |
0 |
2 |
|
5 |
0 |
0 |
0 |
0 |
0 |
8 |
|
6 |
0 |
0 |
0 |
0 |
0 |
0 |
Граф для нахождения кратчайшего пути G2(V,E), где V – множество вершин, а E – множество ребер, представлен на рисунке 2.4.
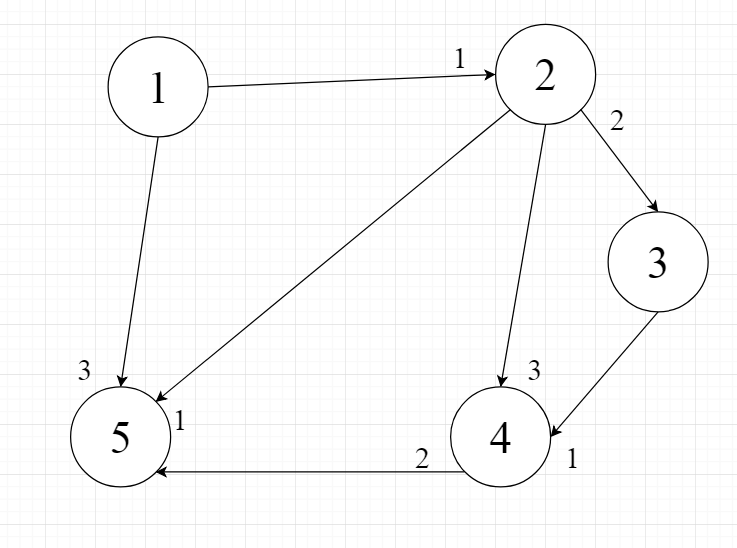
Рисунок 2.4 – Граф для второго задания
Матрица смежности графа G2 приведена в таблице 2.2.
Таблица 2.2 - Матрица смежности
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
0 |
1 |
0 |
0 |
3 |
|
2 |
1 |
0 |
2 |
3 |
1 |
|
3 |
0 |
2 |
0 |
1 |
0 |
|
4 |
0 |
3 |
1 |
0 |
2 |
|
5 |
3 |
1 |
0 |
2 |
0 |
2.7 Результаты работы программы на тестовых данных
Пользователь вводит количество ребер, далее происходит ввод матрицы смежности на экран. Далее пользователь вводит номер стартовой вершины, от которой будет происходить поиск кратчайших путей до остальных вершин с помощью алгоритма Дейкстры.
После ввода указанных в таблице 2.1 данных результатом работы программы будут являться кратчайшие пути до вершин. Результат работы программы представлен на рисунке 2.5.
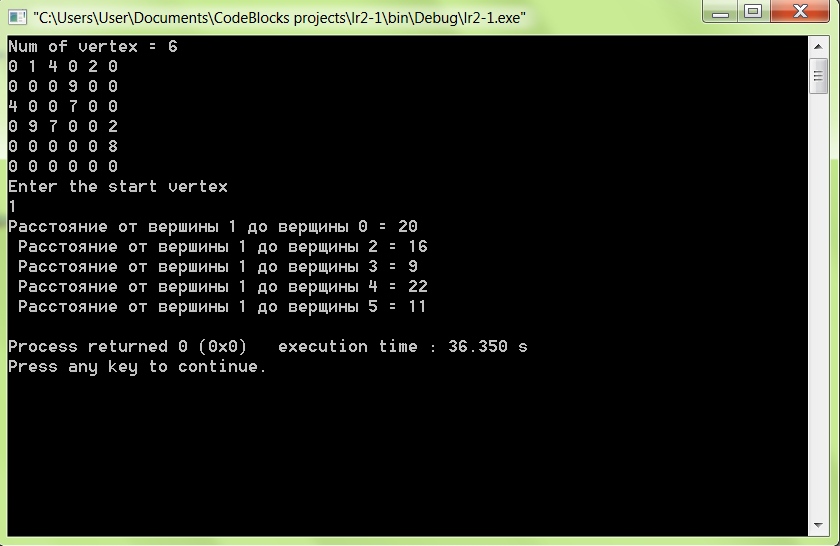
Рисунок 2.5 – Работа первой функции
Пользователь вводит количество ребер, далее происходит ввод матрицы смежности на экран. Далее пользователь вводит номер стартовой вершины, от которой будет происходить поиск кратчайших путей до остальных вершин с помощью алгоритма Примы.
После ввода указанных в таблице 2.2 данных результатом работы программы будут являться кратчайшие пути до вершин. Результат работы программы представлен на рисунке 2.6.
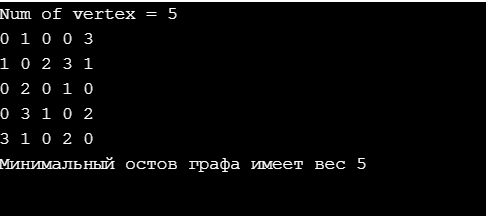
Рисунок 2.6 – Результат выполнения второго задания
3 Заключение
В ходе выполнения данной лабораторной работы были разработаны функции для работы с графами, которые при получении на вход матрицы смежности, производят поиск кратчайших путей из точки, выбранной пользователем в другие вершины и составляет контур минимальной длины.
В лабораторной работе были использованы алгоритмы:
1) для нахождения кратчайшего пути – Дейкстра;
2) для нахождения контура минимальной длины – Прима.
