
Министерство высшего образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ» (ТУСУР)
Кафедра комплексной информационной безопасности электронно-вычислительных систем (КИБЭВС)
ОЦЕНКА АЛГОРИТМИЧЕСКОЙ СЛОЖНОСТИ
Отчет по лабораторной работе №1
по дисциплине «Технологии и методы программирования»
Студентка гр.737-1
______ Агеева В.С
Принял
Руководитель
преподаватель кафедры КИБЭВС
Калмыков М.О.
__________
Томск, 2019
1 Введение
Цель работы:
- оценить алгоритмическую сложность сортировок, реализованных в практических работах №6,7.
2 Ход работы
2.1 Сортировка «Расческа»
На рисунке 2.1 показан вывод программы.
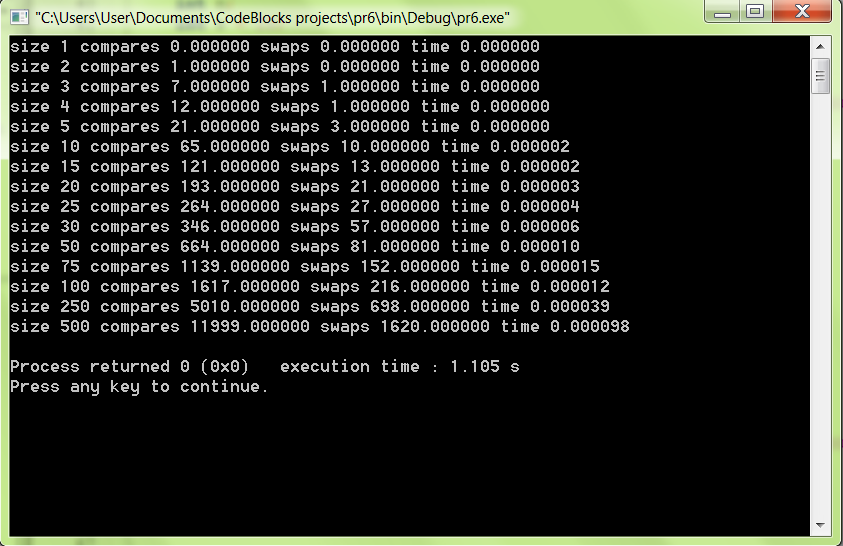
Рисунок 2.1 – Значения выводимой программы
В таблице 2.1 приведены значения размера массивов, количество сравнений для каждой длины (compares) и количество перестановок (swaps).
Таблица 2.1 – Таблица значений количества сравнений и перестановок
|
Размер массива, n |
Количество сравнений |
Количество перестановок |
|
1 |
0 |
0 |
|
2 |
1 |
0 |
|
3 |
7 |
1 |
|
4 |
12 |
1 |
|
5 |
21 |
3 |
|
10 |
65 |
10 |
|
15 |
121 |
13 |
|
20 |
193 |
21 |
|
25 |
264 |
27 |
|
30 |
346 |
57 |
|
50 |
664 |
81 |
|
75 |
1139 |
152 |
|
100 |
1617 |
216 |
|
250 |
5010 |
698 |
|
500 |
11999 |
1620 |
На рисунке 2.2 показана зависимость O(n)=n, O(n)=n*log2(n), O(n)=n2, O(n)=n3, количество сравнений и количество перестановок.
|
|
|
|
|
|
|
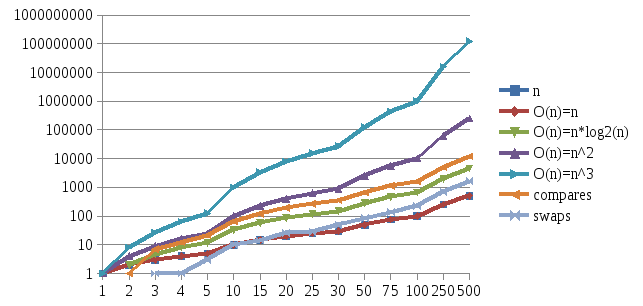
Рисунок 2.2 – Зависимость для сортировки «Расческой»
В таблице 2.2 показаны длина массивов и время выполнения перестановок и сравнений.
Таблица 2.2 – Таблица значений времени
|
Размер массива, n |
Время |
|
1 |
0 |
|
2 |
0 |
|
3 |
0 |
|
4 |
0 |
|
5 |
0 |
|
10 |
0,000002 |
|
15 |
0,000002 |
|
20 |
0,000003 |
|
25 |
0,000004 |
|
30 |
0,000006 |
|
50 |
0,000010 |
|
Продолжение таблицы 2.2 |
|
|
Размер массива, n |
Время |
|
75 |
0,000015 |
|
100 |
0,000012 |
|
250 |
0,000039 |
|
500 |
0,000098 |
На рисунке 2.3 показан график зависимости времени от длины массива.
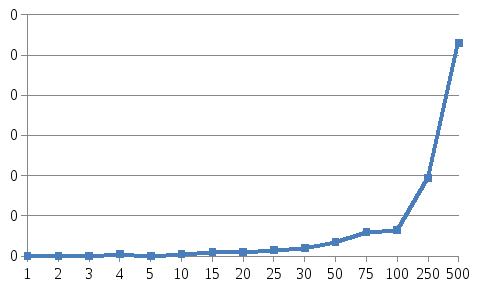
Рисунок 2.3 – График зависимости времени от длины массива
Из данных графиков можно сделать вывод, что линии количества перестановок и сравнений лежит между линией О(n) = n*log2(n). А лучшее время для сортировки расчески = n*log2(n), а худшее = О (n2). Из этого следует, что наша программа попадает в лучшее время.
2.2 Сортировка «Шелла»
На рисунке 2.4 показан вывод программы.
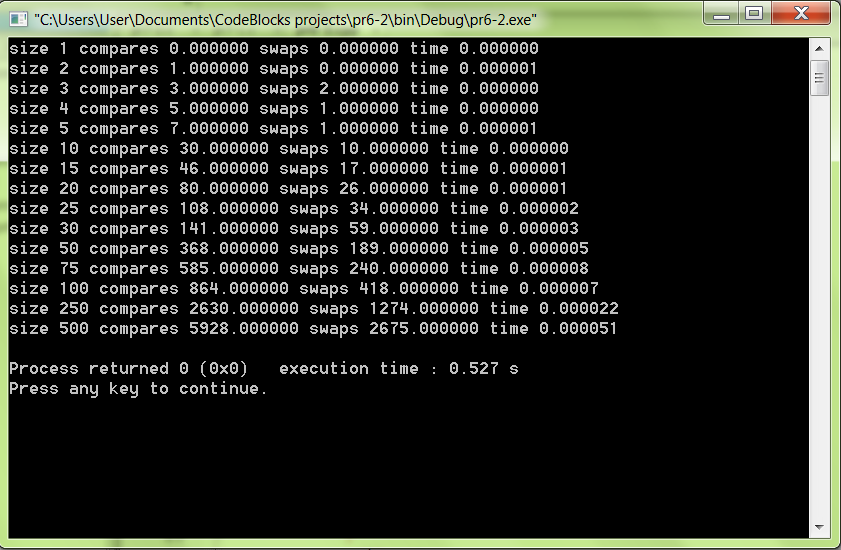
Рисунок 2.4 - Значения выводимой программы
В таблице 2.3 приведены значения размера массивов, количество сравнений для каждой длины (compares) и количество перестановок (swaps).
Таблица 2.3 – Таблица значений количества сравнений и перестановок
|
Размер массива, n |
Количество сравнений |
Количество перестановок |
|
1 |
0 |
0 |
|
2 |
1 |
0 |
|
3 |
3 |
2 |
|
4 |
5 |
1 |
|
5 |
7 |
1 |
|
10 |
30 |
10 |
|
15 |
46 |
17 |
|
Продолжение таблицы 2.3 |
||
|
Размер массива, n |
Количество сравнений |
Количество перестановок |
|
20 |
80 |
26 |
|
25 |
108 |
34 |
|
30 |
141 |
59 |
|
50 |
368 |
189 |
|
75 |
585 |
240 |
|
100 |
864 |
418 |
|
250 |
2630 |
1274 |
|
500 |
5928 |
2675 |
На рисунке 2.5 показана зависимость O(n)=n, O(n)=n*log2(n), O(n)=n2, O(n)=n3, количество сравнений и количество перестановок.
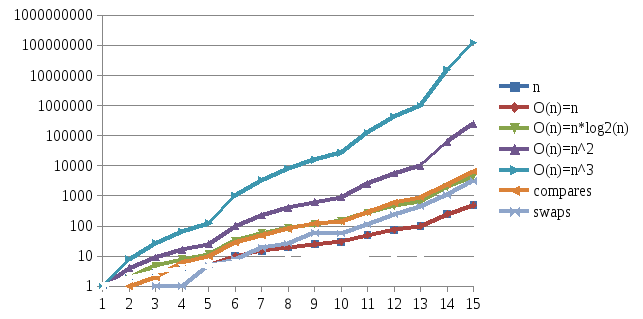
Рисунок 2.5 – Зависимость для сортировки «Шелла»
В таблице 2.4 показаны длина массивов и время выполнения перестановок и сравнений.
Таблица 2.4 – Таблица значений времени
|
Размер массива, n |
Время |
|
1 |
0 |
|
2 |
0,000001 |
|
3 |
0 |
|
4 |
0 |
|
5 |
0,000001 |
|
10 |
0 |
|
15 |
0,000001 |
|
20 |
0,000001 |
|
25 |
0,000002 |
|
30 |
0,000003 |
|
50 |
0,000005 |
|
75 |
0,000008 |
|
100 |
0,000007 |
|
250 |
0,000022 |
|
500 |
0,000051 |
На рисунке 2.6 показан график зависимости времени от длины массива.
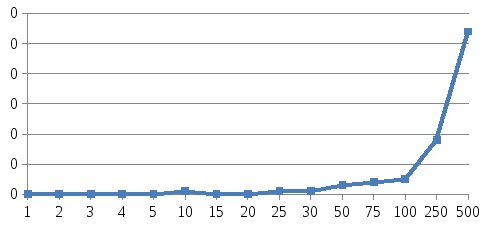
Рисунок 2.6 – График зависимости времени от длины массива
Из данных графиков можно сделать вывод, что линии количества перестановок и сравнений лежит между линией О(n) = n*log2(n). А лучшее время для сортировки Шелла = n*log2(n), а худшее = О (n2). Из этого следует, что наша программа попадает в лучшее время.
