Лекция - ОТНОШЕНИЯ

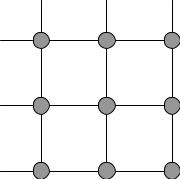
ОТНОШЕНИЯ

Понятие отношения используют для обозначения связи между объектами или понятиями.

Декартовым произведением множеств А В называют третье множество С, элементами которого служат пары всех элементов множеств А и В, при этом первый элемент берется из множества А, второй – из множества В.

Пример.

А = {a1, a2, a3}; B = {b1, b2, b3}.

A B = {<a1, b1>, <a2, b1>, <a3, b1>, <a2, b1>, <a2, b2>, <a2, b3>, <a3, b1>, <a3, b2>, <a3, b3>}.

Сопоставим с декартовым произведением двух множеств прямоугольную решетку, узлы которой взаимно однозначно соответствуют элементам декартова произведения (см. рисунок 2.1)

b1 b1

b2

b3

Рисунок 1. Решетка декартова произведения

Декартовым произведением n множеств А1, А2, …, Аn

называют множество С = А1 А2 … Аn.

Каждый элемент С рассматривается как упорядоченное

множество

сi = < ai1, ai2, …, ain>,

называемое кортежем.

Кортеж состоит из компонент, для которых задается местоположение. Кортеж может иметь одинаковые компоненты. Число компонент кортежа называют его длиной. Два кортежа считаются равными, если их длина одинакова и соответствующие компоненты равны между собой. Компонентами кортежа могут быть любые объекты, в том числе множества и кортежи.

Примеры.

квадрата Т Х2. Совокупность множества Х с заданным в нем бинарным отношением Т Х2 называется графом G.

G = (X, T),

где Х – множество вершин (носитель графа); Т – множество дуг (сигнатура графа).

Пусть задано декартово произведение А В. И пусть с А В,

с = <x, y>, x A, y B.

Проекцией элемента с на множество А назовем элемент х. Сечением R A B по элементу х А называется множество

элементов у В таких, что <x, y> R, R А B.

Вместо термина сечение часто употребляется термин

окрестность единичного радиуса.

Множество всех сечений, взятых для всех элементов множества А при задании на нем отношения R А B, называется

фактормножеством.

Фактормножество полностью определяет отношение R. Рассмотрим предыдущий пример. Пусть Х А, и Х = {2, 7}.

Тогда сечение R(X) = R(2) R(7) = {1, 2} {1} = {1, 2}. Фактор-

множество определяется как множество всех сечений R по всем элементам из А. Зададим фактормножество в виде двух строк, в первой из которых поместим элементы множества А, а во второй под каждым элементом запишем сечение по этому элементу.

Вторая строка задает фактормножество. Сечение и фактормножество наглядно представлены решеткой на рисунке 2.2.

1. Операции над отношениями

Для бинарных отношений обычным образом определены те- оретико-множественные операции объединения, пересечения и др.

Пусть R1 А С отношение из А в С, а R2 С В – отношение из С в В.

Композицией двух отношений R1 и R2 называется отношение R А В из А в В, определяемое следующим образом:

R = R1 ○ R2 = {<a, b>| cуществует С такое, что <a, c> R1 и

<c, b> R2}.

Обратным отношением для R называется отношение

R1 = {<a, b> | <b, a> R}.

Для любых бинарных отношений выполняются свойства:

Свойство 1:

(R–1)–1 = R.

Cвойство 2: Пусть S, R – отношения, тогда

(S, R)–1 = R–1 ○ S–1.

Свойство 3: Если R S и T Y, то

T R Y S.

Функция f : A → B может быть определена как отношение, определенное на множестве А В, обладающее свойством:

Если (a, b) f и (a, c) f, то b = c.

Область определения функции обозначается как Df, а

область ее значений как Rf.

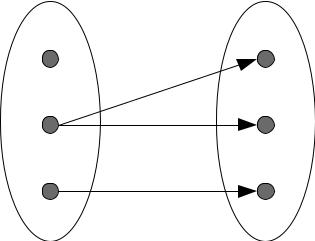
Если Df = А и Rf В, то говорят, что функция f задана на множестве А со значениями во множестве В и осуществляет отображение множества А в множество В. Вместо <a, b> f, пишут b = f(a), здесь b – значение функции, соответствующее аргументу а. Необходимо обратить внимание, что не каждое отношение является функцией (см. рисунок 2.5).

Рисунок 5. Отношение, но не функция

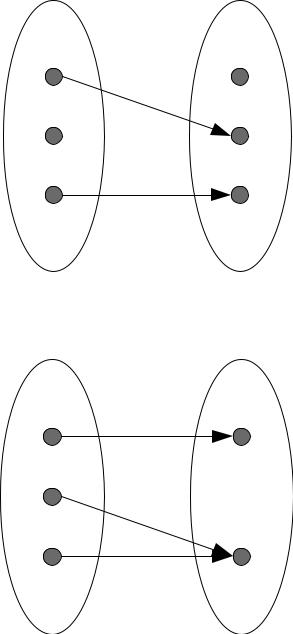
Пусть f : A → B. Функция называется инъективной, если для

любых а1, а2, b из b = f(a1) и b = f(a2) следует, что a1 = a2 (рисунок

2.6).

Функция f называется сюръективной, если для любого

Рисунок 6. Инъективная функция

Рисунок 7. Сюръективная функция

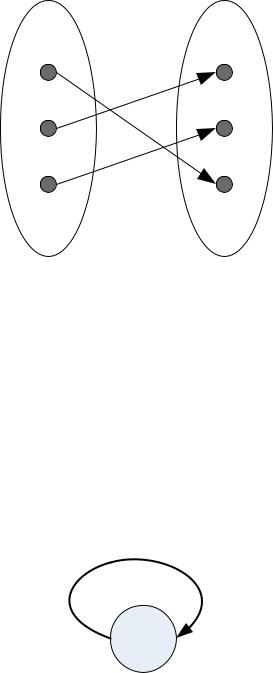
Функция f называется биективной, если f одновременно сюръективна и инъективна (см. рисунок 2.8).

Если существует биективная функция f : А → В, то говорят, что f осуществляет взаимнооднозначное соответствие между множествами А и В.

Рисунок 8. Биективная функция

2. Свойства бинарных отношений

Рассмотрим наиболее важные свойства бинарных отношений. Пусть задано множество А, А А = А2 и отношение R на нем.

Отношение R в множестве А называется рефлексивным, если для каждого элемента а А справедливо утверждение a R a. Если изображать рефлексивность графически, то элемент имеет петлю (см. рисунок 2.9).

а

Рисунок 9. Рефлексивное отношение

Если для каждого элемента а А справедливо утверждениеa R a, то отношение называется антирефлексивным.

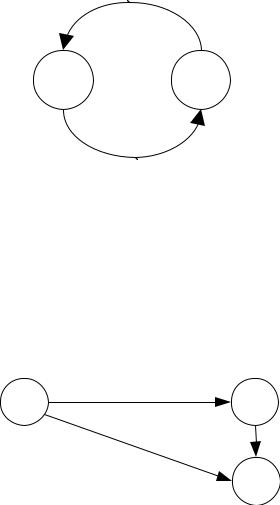
Отношение R в множестве А называется симметричным, если для любых а, b A выполнено: a R b следует b R a; или (a,b) R

(b, a) R, a b.

Графически симметричность можно изобразить следующим образом (см. рисунок 2.10).

Рисунок 10. Симметричное отношение

Если для любых а, b A выполнено: a R b b R a следует a = b, то такое отношение называется антисимметричным.

Отношение R называется транзитивным, если для любых a, b, c А, выполняется: a R b и b R c a R c, при этом a b, b c, a с. Граф, представляющий транзитивное отношение R, выглядит следующим образом (см. рисунок 2.11):

а b

с

Рисунок 11. Транзитивное отношение

При этом дуга (а, с) называется транзитивно замыкающей дугой.

Бинарное отношение R в множестве А, обладающее свойствами:

рефлексивности: для каждого a A, (a, а) R; транзитивности: для любых a, b, с A следует (a, b) R,

(b, с) R (a, с) R,

называется отношением упорядоченности и обозначается .

Если любые два элемента а, b упорядоченного множества находятся в отношении упорядоченности a b или b a, то это множество называется линейноупорядоченным, в противном случае – частично упорядоченным.

Например, отношение a b на множестве действительных чисел является отношением упорядоченности. Во множестве подмножеств некоторого универсального множества U отношение А В также есть отношение упорядоченности. Схема организации

подчинения в учреждении есть отношение частичного порядка на множестве должностей.

Бинарное отношение в множестве А, обладающее свойствами антирефлексивности, антисимметричности и транзитивности, назы-

вается отношением строгой упорядоченности и обозначается <.

Рассмотрим отношение включения . Это отношение

антисимметрично, если Ai Aj и Aj Ak, то Ai Ak, т. е. отношениетранзитивно и является отношением упорядоченности . Множество А с заданным на нем отношением упорядоченности называется упорядоченным этим отношением. Отношение включение является частично упорядоченным множеством.

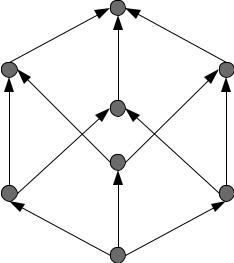
Частично упорядоченное множество изображают в виде графов G = (X, U). Например, пусть А = {1, 2, 3}. Рассмотрим отношение быть подмножеством. Получаем следующую диаграмму (удалены петли и транзитивно замыкающие дуги), называемую

диаграммой Хассе (см. рисунок 2.12).

Понятие непосредственного старшего легко задается в частично упорядоченном множестве следующим определением: ai покрывает aj. Это означает, что aj < ai и не найдется такого элемента аk, что aj < ak < ai. Если рассмотрим подмножество A A и

любого элемента aj A , то элемент a называется минорантой подмножества A .

{1,2,3}

{2,3}

{1,3}

{1,2}

{3}

{0}

Рисунок.12. Пример диаграммы Хассе

Если отношение R, определенное на множестве А, является рефлексивным, симметричным и транзитивным, то его называют

отношением эквивалентности.

Классом эквивалентности, порожденным элементом х,

называется подмножество множества Х, состоящее из тех

эквивалентности Е существуют четыре класса эквивалентности

[0] = {0}, [1] = {1}, [2] = {2}, [3] = {3}.

Отношение принадлежности к одной студенческой группе на множестве студентов института – это отношение эквивалентности, и классом эквивалентности является множество студентов одной группы.

Необходимо заметить, что класс эквивалентности порождается любым своим элементом. Классы эквивалентности, соответствующие отношению эквивалентности R, определенному на множестве А, разбивают множество А на конечное число непустых непересекающихся множеств.

Например, определим отношение R на множестве натуральных чисел следующим образом: