Measurement and Control Basics 3rd Edition (complete book)

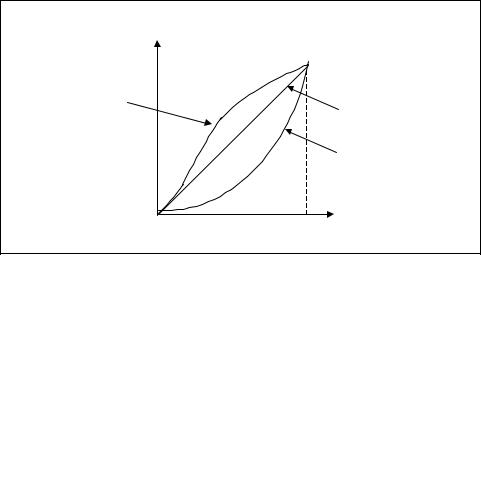
quently used characteristics are quick opening, linear, and equal percentage, as shown in Figure 10-2.

% Flow

100

Quick opening

Linear

Equal percentage

Figure 10-2. Flow characteristic curves of common valves

The quick-opening valve is predominantly used for on/off control applications. A relatively small movement of the valve stem causes the maximum possible flow rate through the valve. For example, a quick-opening valve may allow 85 percent of the maximum flow rate with only 25 percent stem travel.

The linear valve has a flow rate that varies linearly with the position of the stem. This relationship can be expressed as follows:

The equal percentage valve is manufactured so that a given percentage change in the stem position produces the same percentage change in flow. Generally, this type of valve does not shut off the flow completely in its limit of travel. Thus, Qmin represents the minimum flow when the stem is at one limit of its travel. At the fully open position, the control valve

278 Measurement and Control Basics

allows a maximum flow rate, Qmin. So we define a term called rangeability (R) as the ratio of maximum flow (Qmax) to minimum flow (Qmin):

Example 10-1 shows how to determine the rangeability of a typical equal percentage valve.

EXAMPLE 10-1

Problem: An equal percentage valve has a maximum flow of 100 gal/min and a minimum flow of 2 gal/min. Find its rangeability (R).

Solution: The rangeability is as follows:

R = Qmax

Qmin

= 100gal / min =

R 50 2gal / min

Control Valve Actuators

Control valve actuators translate a control signal (normally 3 to 15 psi or 4 to 4 ma) into the large force or torque that is needed to manipulate a valve. There are two common types of actuators: electric and pneumatic. Electric motor actuators are used to control the opening and closing of smaller rotary-type valves such as butterfly valves. However, pneumatic actuators are used more widely because they can effectively translate a small control signal into a large force or torque. The force generated by the pneumatic valve actuator is based on the definition of pressure as force per unit area:

If we need to double the force for a given pressure, we only need to double the area over which the pressure is applied. Very large forces can be developed by the standard 3-15 psi (20 – 100 KPa) control signal. Many types of

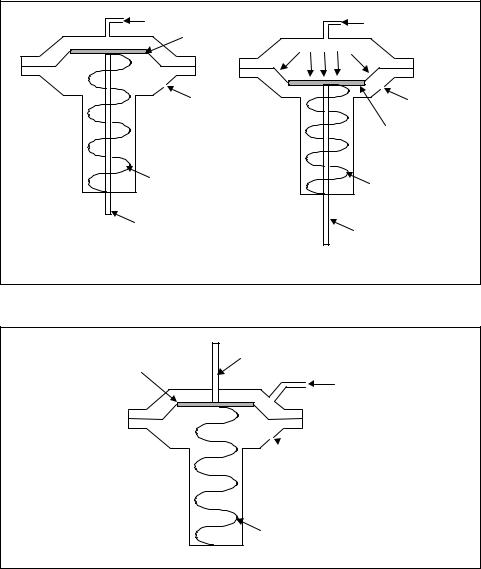
pneumatic valve actuators are available, but the most common is the diaphragm type shown in Figure 10-3. The pneumatic diaphragm valve actuator can be designed as a direct-acting type (as shown Figure

10-3) or as reverse-acting (as shown in Figure 10-4).

Figure 10-3. Direct-acting pneumatic valve actuator

Valve shaft

Diaphragm

Pressure In

Air hole

Spring

Figure 10-4. Reverse-acting pneumatic valve actuator

Figure 10-3a shows the actuator with a low-pressure (3 psi) signal applied. This signal ensures that the spring maintains the diaphragm and the connected valve shaft in the position shown. The pressure on the opposite or spring side of the diaphragm is maintained at atmospheric pressure because there is a hole opened to the atmosphere on the bottom right side

280 Measurement and Control Basics

of the actuator. Increasing the control signal pressure applies a force on the diaphragm that moves the diaphragm and the connected valve shaft down against the spring. Figure 10-3b shows this action in a case where the maximum control signal of 15 psi (100 pascals) produces the maximum travel for the valve shaft.

The pressure and force applied are linearly related, as given by F = ∆ PA. The compression of the spring is linearly related to force according to Hooke’s law, as follows:

So, the shaft position is linearly related to the applied control pressure by the following:

A reverse-acting pneumatic diaphragm valve actuator is shown in Figure 10-4. When a pressure signal is applied, the valve shaft moves in the direction opposite that of the direct-acting actuator, but it follows the same operating principle. In the reverse-acting actuator, the valve shaft is pulled into the actuator by the application of a pressure control signal.

Example 10-2 provides a typical calculation for sizing the diaphragm of a valve actuator.

Valve Sizing for Liquids

Sizing a control valve incorrectly is a mistake both technically and economically. A valve that is too small will not pass the required flow, and this will impact the process. A valve that is oversized will be unnecessarily expensive, can lead to instability, and can make it more difficult to control flow in a process.

EXAMPLE 10-2

Problem: Assume that a force of 500 N is required to fully open a control valve that is equipped with a pneumatic diaphragm valve actuator. The valve input control signal for the actuator has a range of 3 to 15 psi (20 to 100 kPa). Find the diaphragm area that is required to fully open the control valve.

Solution: The area is calculated using Equation 10-3, as follows:

F = ∆ PA

Since the pressure signal required to open the valve fully is 100 kPa we have the following:

To select the correct-sized valve for a given application you must know what process conditions the valve will actually encounter in service. The technique used to size control valves is a combination of fluid flow theories and flow experimentation.

Daniel Bernoulli was one of the first scientists to take an interest in the flow of liquids. Using the principle of conservation of energy, he discovered that as a liquid flows through an orifice the square of the fluid velocity is directly proportional to the pressure differential across the orifice and inversely proportional to the density of the fluid. In other words, the greater the pressure differential, the higher the velocity; the greater the fluid density, the lower the velocity. Equation 10-6 gives this relationship:

In addition, as we saw in Chapter 9, you can calculate the volumetric flow of liquid by multiplying the fluid velocity by the flow area, or Q = Av. As a result, the volumetric flow through an orifice is given by the following:

If Equation 10-7 is expressed in U.S. engineering units, then volumetric flow (Q) is in gallons per minute (gpm), pressure differential (∆P) is in psi, and specific gravity (G) and the flow area (A) are in square inches. Letting

282 Measurement and Control Basics

the constant (C) account for the proper units of flow we obtain the following:

Although Equation 10-8 has a strong theoretical foundation, it does not take into account the energy losses caused by turbulence and friction as the fluid passes through the orifice. We can compensate for this by adding a discharge coefficient (Cd) that is different for each type of flow orifice:

Since the flow area is also a unique function of each type of flow orifice, we can combine all three of these terms into a single coefficient. When applied to valves, this coefficient is called the valve-sizing coefficient (Cv). Replacing the three terms Cd, C, and A with Cv we obtain the equation for liquid flow through a control valve:

Example 10-3 illustrates how to calculate the volumetric flow through a control valve.

EXAMPLE 10-3

Problem: Water flows through a 2-in. control valve with a pressure drop of 4 psi. Find the volumetric flow rate if the control valve has a Cv of 55.

Solution: Using Equation 10-10,

we obtain the following:

Q = 55 4 gpm = 110gpm

1

The valve-sizing coefficient Cv is experimentally determined for each different size and style of valve by using water in a test line under carefully

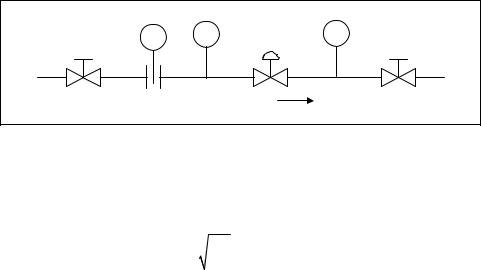
controlled standard conditions. Figure 10-5 shows the standard test piping arrangement established by the Fluid Controls Institute (FCI) to measure Cv data uniformly. Using this test setup, control valve manufacturers determine and publish Cv valves for their valves. These published Cv make it relatively easy to compare the capacities of the various valves offered by manufacturers.

Figure 10-5. Test piping for Cv measurements

To determine the Cv for a valve that controls the flow of water or other liquids that behave like water, we rearrange the liquid valve sizing equation (Equation 10-10) as follows:

This equation is based on ideal liquids, but viscous conditions can result in significant sizing since manufacturers’ published Cv values are based on test data using water. Although most valve applications involve liquids whose viscosity corrections can be ignored, you should consider liquid viscosity in each application that requires you to select a valve.

A careful review of the basic valve liquid flow equation (Equation 10-10) will help you develop a feel for what Cv really means. Consider a case where water at 60°F flows through a valve. Here the specific gravity (G) is equal to 1. Let's also assume that a 1-psi pressure differential is maintained across the valve. Under these conditions, the entire square root factor becomes 1. This specific example shows that Cv is numerically equal to the number of U.S. gallons of water that will flow through the valve in one minute when the water temperature is 60°F and the pressure differential across the valve is 1 psi. Thus, Cv provides an index for comparing the liquid flow capacities of different types of valves under a standard set of operating conditions.

The valve-sizing coefficient Cv varies with both the size and style of valve. By combining published Cv data, the basic liquid sizing equation, and your actual service conditions, you can select the correct valve size for any