3. Математические модели вибрации

При решении вибрационных задач используются различные математические модели реальной вибрации.

В основу большинства моделей основных составляющих вибрации положено представление их в виде узкополосного процесса с медленно изменяющейся во времени амплитудой и фазой.

В основу моделирования широкополосной вибрации положено представление ее в виде линейного наложения основных составляющих и вибрационного шума. Рассмотрим несколько возможных моделей вибрации ГТД.

3.1 Модель I. Квазидетерминированная вибрация

Такая вибрация представляет собой вырожденный случайный процесс, реализации которого описываются функциями времени определенного вида, содержащими один или несколько случайных параметров, не зависящих от времени. Пусть реализации отдельных составляющих вибрации представляют собой гармоническое колебание со случайной начальной фазой. Тогда ансамбль реализаций каждой составляющей имеет вид:

, (11)

где и фиксированы. Предположим, что фаза распределена равномерно на периоде :

. (12)

Корреляционная функция вибрации (11) представляет собой гармоническое колебание той же частоты (рис. 4):

, (13)

а спектральная плотность представляется одной дискретной линией на частоте :

, (14)

где - дельта-функция Дирака.

Рис. 4 Характеристики квазидетерминированной вибрации.

Широкополосная квазидетерминированная вибрация может содержать несколько гармонических составляющих (11), т.е. представляет собой полигармонический процесс:

, (16)

у которого один или несколько параметров случайны.

Спектрально-временные характеристики такой вибрации показаны в нижней части на рис. 4. На графике штриховой линией показана частотная характеристика фильтра, выделяющего составляющие, и вид составляющих на выходе фильтра. Реализации составляющих квазидетерминированной вибрации могут отличаться также частотами или амплитудами. В последнем случае, например, одномерная плотность вероятности принимает вид:

, (17)

где – закон распределения амплитуд реализаций.

3.2 Модель II. Квазигармоническая вибрация

Отдельные составляющие суммарной вибрации представляют собой узкополосную вибрацию и по форме напоминают модулированное гармоническое колебание, почему и названы квазигармоническими. Квазигармоническая вибрация возникает, например, при воздействии широкополосной случайной вибрации на колебательную систему с одной степень свободы при слабом демпфировании. Если возбуждающая широкополосная вибрация стационарна и нормальна, то стационарной и нормальной будет и квазигармоническая вибрация динамической системы.

Спектральная плотность квазигармонической вибрации сконцентрирована вокруг собственной частоты :

, (18)

а корреляционная функция представляет собой затухающее колебание частоты :

. (19)

Здесь - спектральная плотность возбуждения системы;

- коэффициент демпфирования динамической системы.

Одномерная плотность вероятности нормальной квазигармонической вибрации описывается законом Гаусса:

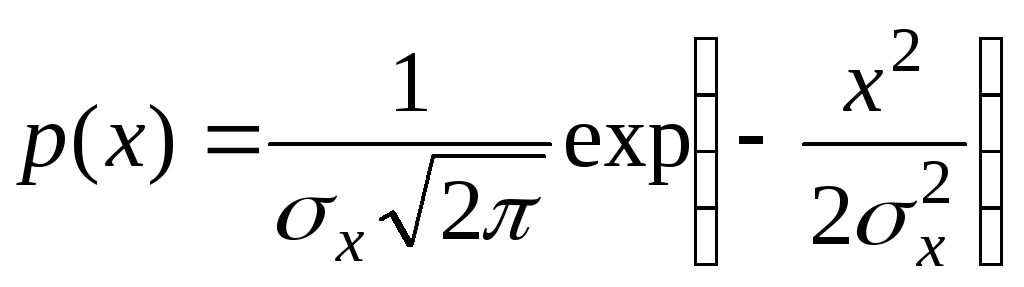. (20)

Огибающую можно определить в виде:

. (21)

Одномерная плотность вероятности огибающей описывается распределением Релея:

. (22)

Среднее значение огибающей:

. (23)

Среднеквадратичное значение:

. (24)

Среднеквадратичное отклонение огибающей:

. (25)

Коэффициент вибрации амплитуд:

. (26)

Справедливо и обратное утверждение: если огибающая квазигармонической вибрации не подчиняется закону Релея, то такая вибрация не нормальна.

Спектрально-временные характеристики ее показаны на рис. 5.

Рис. 5. Характеристики нормальной квазигармонической вибрации.