
- •Министерство сельского хозяйства рф
- •Часть I
- •Пермь 2008
- •Задание 3. Группировка по двум признакам и построение комбинационной таблицы
- •1. Выписать исходные данные об урожайности зерновых культур из предыду-
- •Задание 12. Определение индивидуального и агрегатного индекса физического объема продукции
- •Задание 13. Индексный анализ реализации продукции хозяйства
- •Задание 14. Определение доверительного интервала для генеральной средней
- •Задание 16. Определение численности выборки
- •Задание 17. Определение доверительной вероятности
- •Cтатистическая проверка гипотез Задание 19. Проверка гипотезы о соответствии фактического распределения нормальному
- •Корреляция
- •Коэффициента корреляции
- •Задание 23. Определение тесноты связи с помощью коэффициента корреляции рангов.
Корреляция
Задание 22. Определение показателей регрессии связи при парной линейной зависимости
Условие. На основе данных табл. 3 найти параметры уравнения парной регрессии ух = а + b·х и вычислить показатели тесноты связи между урожайностью и одним из факторных признаков.
Методика выполнения:
1. Выписать из табл. 3 данные об урожайности зерновых культур (у) и величины факторного признака (х) в табл. 24.
2. Для определения формы и направления связи построить корреляционное поле (рис.6)
 у
у

х
Рис. 6 – Влияние ………………………….. на урожайность
Таблица 24 – Вычисление величин для уравнения регрессии и расчета
Коэффициента корреляции
Номера хозяйств |
у |
х |
ху |
Квадраты |
|
х2 |
у2 |
||||
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
|
|
|
|
|
Сумма |
|
|
|
|
|
Вычислить произведение ху, х2, у2 и их суммы.
Составить нормальные уравнения:
у na + bх
ху = ах + bх2
5.
Вычислить значение параметров уравнения
«а» и «b»: b =
![]() ;
;
а
=
![]() -
b
-
b
6. Записать уравнение регрессии, выражающее связь между урожайностью зерновых и величиной факторного признака х : ух = а + b х
7.
Определить тесноту связи между
анализируемыми факторами путем расчета
линейного коэффициента парной корреляции
по формуле: r
=
![]() , где
, где
![]()
![]() ;
;
![]()
8.
По вычисленному коэффициенту корреляции
определить эмпирический коэффициент
детерминации, который показывает долю
влияния на результат факторного признака:
r2yx
=
![]()
9.
Вычислить коэффициент эластичности :
Э = b
![]() , который показывает процентное отношение
результата при изменении факторного
показателя на 1 %.
, который показывает процентное отношение
результата при изменении факторного
показателя на 1 %.
10.После
определения параметров уравнения и
расчета коэффициента корреляции
произвести оценку статистической
надежности по критерию Фишера уравнения
в целом по формуле : Fфакт.
=
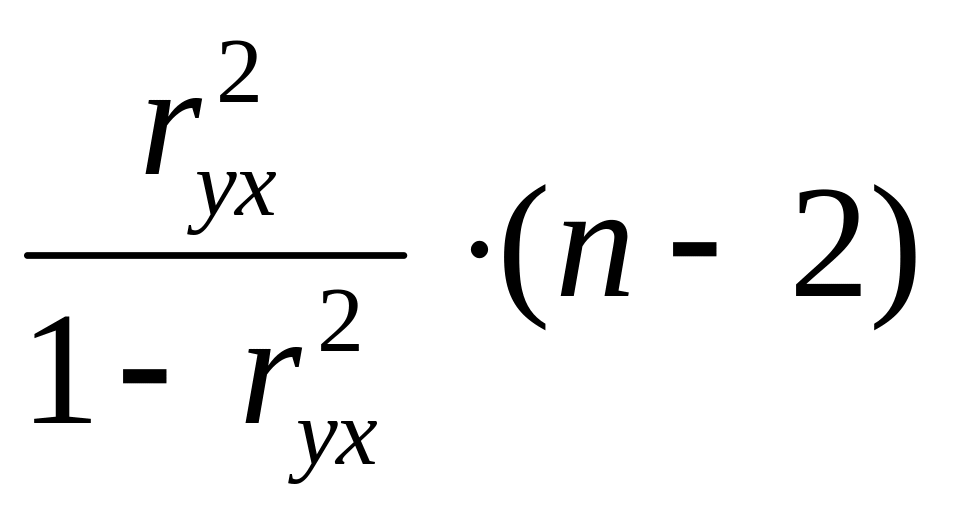 ,
где n
– численность единиц в совокупности.
,
где n
– численность единиц в совокупности.
11.Полученное значение Fфакт. сравнивается с табличным значением Fтабл. при уровне вероятности 0,05 и числе степеней свободы факторной дисперсии, равной 1, и остаточной, равной (n – 2). При Fфакт. > F0,05 нулевая гипотеза об отсутствии связи отклоняется и делается вывод о статистической надежности уравнения связи.
12.Оценить
статистическую значимость коэффициента
регрессии «b» и корреляции «r»
по критерию Стьюдента t
b
и t
r
, которые связаны с найденным значением
Fфакт.
и равны t
b
= t
r
=
![]() ;
;
13.Вычисленные фактические коэффициенты t b и t r сравниваются с табличными их значениями при уровне значимости 0,05 и числе степеней свободы
n – 2 . При t фак. > t 0,05 свидетельствует о статистической надежности найденных параметров уравнения.
14.Раскрыть экономическое содержание уравнения ух = а + b·х. . Дать оценку тесноты связи и существенности коэффициентов регрессии и корреляции.
