3 Типовий розв΄язок задач

Завдання 1 Дана З.Л.П.

minZ=3X₁-X₃+X₄-2X₅

X₁-X₂+2X₃+4X₄=11

X₁-X₂+3X₃+6X₄+X₅=19

-2X₁+3X₂-5X₃-11X₄=-26

.

1.Методом Жордана-Гаусса

а) знайти початковий опорний план і обчислити Z( );

б) перейти до іншого опорного плану й обчислити Z( ).

2. Для одного з опорних планів виразити базисні змінні через вільні, перейти від рівностей в обмеженнях задачі до нерівностей і розв’язати задачу геометрично.

3. Виходячи з опорного плану з «гіршою» функцією мети замінити задачу лінійного програмування в канонічній формі та розв’язати її симплекс-методом.

4.Розв’язати вихідну задачу методом штучного базису.

Розв’язок

1.а) усі обчислення за методом Жордана-Гаусса будемо робити в таблиці 6, попередньо помноживши трете рівняння на – 1, щоб b₃=26>0. Позначимо .

Таблиця 6

№ кроку	Ā1	Ā2	Ā3	Ā4	Ā5	Ā0
	1	-1	2	4	0	11
0	1	-1	3	6	1	19
	2	-3	5	11	0	26
	1	-1	2	4	0	11
1	0	0	1	2	1	8
	0	-1	1	3	0	4
	1	1	0	-2	0	3
2	0	1	0	-1	1	4
	0	-1	1	3	0	4
	1	1	0	-2	0	3
3	-1	0	0	1	1	1
	1	0	1	1	0	7

Вибравши a₁₁=1 розв´язувальним елементом, застосуємо формулу прямокутника і перерахуємо елементи нової таблиці на 1-му кроці. При виборі розв´язувального елемента враховуємо дві умови: компоненти A₀ у новій таблиці повинні бути не менші нуля і для спрощення рахунку розв´язувальний елемент повинен бути ближчим до 1, а найкраще– дорівнювати 1. Тому після 1-го кроку для перерахування таблиці розв´язувальний елемент a₃₃=1, тому що в 1 і 2-ому рівняннях уже є базисні змінні X₁ й X₅ (вектори Ā₁ і Ā₅ одиничні). У результаті 2-го кроку були отримані три базисні змінні X₁, X₅ і X₃, яким відповідають базисні одиничні вектори Ā₁, Ā₅, Ā₃. Узявши вільні змінні X₂ = X₄ =0, одержимо початковий опорний план З.Л.П. *=(3;0;4;0;4), якому відповідає функція мети Z₁=3·3-4·1-2·4=-3.

1.б) перейдемо на 3-му кроці до іншого опорного плану. Для цього треба замість якої-небудь базисної змінної ввести іншу. Наприклад, замість X₁ X₂. При цьому розв´язувальний елемент a₁₂=1 і усі компоненти A₀ у новій таблиці >0. У результаті перерахування таблиці одержали після 3-го кроку нові базисні змінні X₂, X₅, X₃ (базисні одиничні вектори Ā₂, Ā₅, Ā₃) і новий опорний план _on=(0;3;7;0;1), що забезпечує функцію мети Z₂=0·3+3·0-7·1+0-2·1= -9.

2. Розв´яжемо задачу геометрично. Це можливо, тому що n – m = 5 – 3 = 2. З огляду на результати, отримані на 3-му кроці, з таблиці 6 маємо систему рівнянь

X₁+X₂ -2X₄ =3; X₂=3-X₁+2X₄≥0

-X₁ +X₄+X₅=1; => X₅=1+X₁-X₄≥0

X₁ +X₃+ X₄ =7; X₃=7-X₁-X₄≥0

X_i≥0, і=1,…,5.

Виразимо Z через X₁ і X₄ , з огляду на отримані вирази базисних змінних X₂, X₅, X₃ через вільні X₁ і X₄

Z=3X₁-(7-X₁-X₄)+X₄-2(1+X₁-X₄)=-9+2X₁+4X₄ .

Тоді розв'язувана З.Л.П. має вид

min Z=-9+2X₁+4X₄; -9+ minZ₁=2X₁+4X₄

X₁-2X₄≤3

-X₁+X₄≤1 X₁≥0

X₁+X₄≤7 X₄≥0

Побудуємо багатогранник розв'язків на площині X₁OX₄ у 1-й чверті.

Граничні прямі: будуємо за двома точками

X1	0	3
X4	-1,5	0

X₁-2X₄≤3: => X₄ 

X1	0	-1
X4	1	0

X₄≤1+X₁ => ℓ₂: X₄=7-X₁;

X1	0	7
X4	7	0

X₄≤7+X₁ => ℓ₃: X₄=7-X₁;

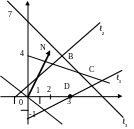
Шукані напівплощини позначимо штрихами. У результаті перетину напівплощин одержуємо багатокутник розв'язків ОАВСД,

рис.1.

Рис.1 Графічне розв΄язання З.Л.П.

Для відшукання min Z₁ будуємо нормальний вектор N = (2;4) і сім´ю рівнобіжних прямих, що задаються Z₁, перпендикулярних N.

Як випливає з рис.1, min Z₁ = Z₁ (0) = Z₁ (0;0) = 2·0+4·0 = 0, то min Z = Z(0) = -9. Для відшукання оптимального плану вихідної задачі підставимо знайдені оптимальні X°₁=X°₄=0 до (1). Одержимо X°₁=0; X°₂=3; X°₃=7; X°₄=0; X°₅=1.

3) розв´яжемо симплекс-методом задачу, розглянуту в попередньому прикладі. За початковий опорний план візьмемо перший опорний план =(3;0;4;0;4), якому відповідає функція мети Z₁=-3 зі значенням, більшим, ніж для другого опорного плану (Z₂=-9). Це дозволить зробити симплексним методом, принаймні, одне перерахування таблиці, тому що неоптимальний.

У цьому випадку ЗЛП має канонічну форму вигляду

X₁+X₂-2X₄ =3

X₂-X₄+X₅ =4

-X₂+X₃+3X₄=4

X_j≥0, (j=1,..,5).

Min Z=3X₁-X₃+X₄-2X₅

Розв´яжемо цю задачу за алгоритмом симплекс-методу. Для цього заповнимо симплекс-таблицю, таблиця 7.

Таблиця 7–Симплекс- таблиця

Баз.	С	Xбаз	3	0	-1	1	-2	Θ0
змін.	базис.		X1	X2	X3	X4	X5
X1	3	3	1	1	0	-2	0	3/4
X5	-2	4	0	1	0	-1	1	4/1
X3	-1	4	0	-1	1	3	0	-
Z	=	-3	0	2	0	-8	0
X2	0	3	1	1	0	-2	0
X5	-2	1	-1	0	0	1	1

Продовження таблиці 7

X3	-1	7	1	0	1	1	0
Z=-9			-2	0	0	-4	0

Обчислюємо й оцінки . Оскільки ∆₂=2>0,то план не оптимальний. Тому шукаємо інший опорний план, уводячи змінну X₂, вектор Ā₂, у базис. Для перерахування таблиці знаходимо симплексне відношення для X₂ Θ₀ = min(3/1; 4/1)=3. Тоді X₁₂ =1 є розв´язувальним елементом. За формулої прямокутника перераховуємо всю таблицю, у тому числі й елементи останнього оцінного рядка. Оскільки всі , то отриманий опорний план =(X₁=0; X₂=3; X₃=7; X₄=0; X₅=1) оптимальний, причому функція мети Z( )=-9.

Зауваження 1. Для простоти перерахування таблиці використовувалась така схема (правило або формула прямокутника (23)), рис.2:

, (23)

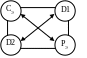
Рис.2 – Схема правила прямокутника

де Н.е –елемент у новій таблиці, що займає ту саму позицію, що і С_е –елемент у старій таблиці;

P_е– розв´язувальний елемент;

D₁ і D₂ –додаткові елементи, що стоять на другій діагоналі прямокутника, якщо вважати, що першу діагональ складають елементи С_е і Р_е.

Зауваження 2. Правило заповнення оцінного рядка для початкової симплекс-таблиці можна для наступних симплекс-таблиць застосовувати з метою перевірки правильності обчислень за формулою прямокутника.

4) розглянемо і розв´яжемо ЗЛП методом штучного базису, наведену в прикладі.

Складемо з вихідної задачі М-задачу. У 2-му рівнянні є базисна змінна X₅, тому туди не додаємо штучну змінну.

MinZ=3X₁-X₃+X₄-2X₅+M(X₆+X₇)

X₁-X₂+2X₃+4X₄+X₆=11

X₁-X₂+3X₃+6X₄+X₅=19

2X₁-3X₂+5X₃+11X₄+X₇=26

Xj≥0 , .

Запишемо дані в симплекс-таблицю, таблиця 8, і заповнимо оцінні рядки 4 і 5 за формулами (24)

. (24)

Таблиця 8 – Симплекс-таблиця М­– задачі

			3	0	-1	1	-2	М	М
Xb	Cb	(Xb)i	X1	X2	X3	X4	X5	X6	X7	Θ
X6	M	11	1	-1	2	4	0	1	0	11/4
X5	-2	19	1	-1	3	6	1	0	0	19/6
X7	M	26	2	-3	5	11	0	0	1	26/11
БезM	Z	-38	-5	2	-5	-13	0	0	0	∆'j
СМ	Z	37	3	-4	7	15	0	0	0	∆''j
Х6	M	17/11	3/11	1/11	2/11	0	0	1	-4/11	17/3
X5	-2	53/11	-1/11	7/11	3/11	0	1	0	-6/11
X4	1	26/11	2/11	-3/11	5/11	1	0	0	1/11	26/2
БезM	Z	80/11	-29/11	-17/11	10/11	0	0	0	13/11	∆'j
CM	Z	17/11	3/11	1/11	2/11	0	0	0	-15/11	∆''j
X1	3	17/3	1	1/3	2/3	0	0	11/3	-4/3	17/2
X5	-2	16/3	0	2/3	1/3	0	1	1/3	-2/3	16
X4	1	4/3	0	-1/3	1/3	1	0	-2/3	-1/3	4
БезM	Z=	23/2	0	-2/3	8/3	0	0	29/3	7/3	∆'j
CM	Z=0	0	0	0	0	0	0	1	1	∆''j
X1	3	3	1	1	0	-2	0			3/1
X5	-2	4	0	1	0	-1	1			4/1

Продовження таблиці 8

X3	-1	4	0	-1	1	3	0			-
Z	=	-3	0	2	0	-8	0			∆j
X2	0	3	1	1	0	-2	0
X5	-2	1	-1	0	0	1	1
X3	1	7	1	0	1	1	0
Z		-9	-2	0	0	-4	0			∆j

У 5-му (m+2) рядку є оцінки ∆''_j >0 (∆₁=3;∆₃=7;∆₅=15)

Тому опорний план М-задачі не оптимальний. Оскільки ∆₅=15 (оцінка з М) найбільша, то X₄ введемо в базис. Знайдемо для X₄ симплексне відношення Θ₀=min(11/4;19/6;26/11)=26/11.

Тому розв´язувальний елемент дорівнює 11 і X₇ виводимо з базису. Для цього перераховуємо таблицю, застосовуючи симплексний алгоритм, і так далі.

Після двох перерахувань таблиці або двох ітерацій у базисі не залишиться штучних змінних, базисні змінні X₁,X₄,X₅ ,m+2 (п'ятий) рядок відкидаємо й аналіз проводимо за четвертим рядком. Оскільки ∆₃=8/3>0, то отриманий опорний план не оптимальний і в базис уводимо змінну X₃ (вектор А₃) замість X₄, Θ₀=min(17/2;16;4)=4.

Розв´язувальний елемент дорівнює 1/3. Після перерахування таблиці одержуємо, що опорний план з базисними змінними не оптимальний, тому що ∆₂=2>0. Тому X₂ вводимо як нову базисну змінну замість X₁, бо Θ₀=min(3/1;4/1)=3.

У результаті перерахування симплекс–таблиці одержали оптимальний план ⁰=(X⁰₁=0; X⁰₂=3; X⁰₃=7; X⁰₄=0; X⁰₅=1), тому що всі ∆j≤0, що забезпечує

min Z=Z( ⁰)= –9.

Завдання 2 Задача про розподіл ресурсів

Підприємство може виготовляти чотири види продукції П-1, П-2, П-3, П-4. Збут будь-якого її обсягу забезпечений. Норми витрати ресурсів і прибуток від одиниці кожного виду продукції надані в таблиці 9. Виконати економічний аналіз лінійної моделі:

1) побудувати модель вихідної та двоїстої задач, знайти оптимальні плани x⁰ і y⁰;

2) дати економічне тлумачення основних і додаткових змінних вихідної та двоїстої задач;

3) проаналізувати доцільне розширення асортименту продукції за рахунок включення нової продукції П₅;

4) установити діапазони зміни вихідних даних за ресурсами і ціною од. продукції, за яких структура оптимального плану не змінюється.

Таблиця 9– Дані задачі розподілу ресурсів

Обсяг ресурсів: трудових, матеріальних, верстатних	Норми витрат ресурсів на од. продукції				Нова продукція
	П-1	П-2	П-3	П-4	П-5
3000	3	4	4	5	5
5000	2	0	3	4	6
8000	10	12	10	8	9
Ціна од. продукції	46	12	10	8	50

Розв’язок

1.Складемо математичні моделі вихідної та двоїстої задач, позначивши через план випуску j-го виду продукції, а через вартість одиниці i-го ресурсу. Тоді за формулами [2;3;5] математичні моделі вихідної та двоїстої задач мають вигляд:

вихідна задача двоїста задача

max=46X₁+12X₂+10X₃+8X₄ min f =3000У₁+5000У₂+8000У₃

3X₁+4X₂+4X₃+5X₄≤3000 3У₁+2У₂+10У₃≥46

2X₁+3X₃+4X₄≤5000 4У₁+12У₃≥12

10X₁+12X₂+10X₃+8X₄≤8000 4У₁+3У₂+10У₃≥10

5У₁+4У₂+8У₃≥8

X_j0 Y_i0

Для рішення симплекс-методом перейдемо в обмеженнях до рівностей шляхом уведення додаткових змінних

вихідна задача двоїста задача

max=46X₁+12X₂+10X₃+8X₄+0(X₅+X₆+X₇) min f =3000У₁+5000У₂+8000У₃

3X₁+4X₂+4X₃+5X₄+X₅ =4000 3У₁+2У₂+10У₃-У4 =46

2X₁+3X₃+4X₄+X₆ =5000 4У₁+12У₃ -У5 =12

10X₁+12X₂+10X₃+8X₄+X₇=8000 4У₁+3У₂+10У₃-У6 =10 X_j0 5У₁+4У₂+8У₃-У7 =8

Y_i0

У вихідній задачі 7 змінних і 3 обмеження, причому додаткові змінні є базисними. Тому цю задачу відразу можна розв´язувати симплекс-методом. У двоїстій задачі 7 змінних і 4 обмеження, причому для розв´язування симплекс-методом треба вводити штучний базис, а це ще плюс 4 змінні. Тому вихідну задачу розв´язувати простіше. Запишемо її дані в симплекс-таблицю 10 і виконаємо розв´язування за алгоритмом симплексного методу. У результаті після однієї ітерації перерахування таблиці одержали в оцінному рядку всі ∆j≥0. Виходить, отриманий опорний план вихідної задачі X₁=800; X₂=X₃=X₄=0; X₅=600; X₆=3400; X₇=0, оптимальний.

Цей план випуску продукції =(800;0;0;0;600;3400;0) забезпечує її максимальну сумарну вартість max Z = 36800 грощ. од.

2. Для того, щоб знайти оптимальний план двоїстої задачі, визначимо взаємозв'язок змінних двоїстих задач і економічний зміст їх додаткових змінних. Для вихідної задачі i- а додаткова змінна

залишок i-го ресурсу для опорного плану вихідної задачі, ,

Таблиця 10–Симплекс-таблиця для задачі розподілу ресурсів

Базис. змін.	Cb	Xb	46	12	10	8	0	0	0	Θo
			X1	X2	X3	X4	X5	X6	X7
X5	0	3000	3	4	4	5	1	0	0	1000
X6	0	5000	2	0	3	4	0	1	0	2500

Продовження таблиці 4

X7		0	8000	10	12	10	8	0	0	1	800
Z =			0	-46	-12	-10	-8	1	0	0
X5	0		600	0	0.4	1	2.6	0	1	-0.3
X6	0		3400	0	-2.4	1	2.4	0	1	-0.2
X1	46		800	1	1.2	1	0.8	0	0	0.1
Z =			36800	0	43.2	36	28.8	0	0	4.6
				У4	У5	У6	У7	У1	У2	У3

i-а змінна двоїстої задачі, означає ціну за одиницю цього ресурсу.

Для двоїстої задачі j-а додаткова змінна,

,

різниця між сумарною вартістю витрат усіх ресурсів y_m+j на одиницю j-го виду продукції та вартістю за одиницю цієї продукції. Тому y_m+j (j=1,…,n) можна трактувати як характеристику рентабельності випуску j-го виду продукції. Якщо y_m+j>0, тоді випуск j-го виду продукції не рентабельний (витрати більші за ціну), якщо y_m+j=0, тоді випуск j-го виду продукції рентабельний. У зв´язку за вищевикладеним, основним змінним однієї задачі відповідають додаткові змінні іншої, тобто

Xn+i Yi

Ym+i Xi

Причому для оптимальних планів цих задач випливає, що

(25)

(26)

З огляду на те, що всі змінні від´ємні, з (25) і (26) одержимо для оптимальних планів

X⁰_n+i=0 y⁰_i>0 чи X⁰_n+i>0 Y⁰_i=0

Y⁰_m+j=0 X⁰_j>0 чи Y⁰_m+j>0 X⁰_j=0

З (6) випливає: для оптимальних планів двоїстих задач:

1) якщо i-й ресурс цілком використовується, (X⁰n+i=0) , тоді його ціна Y⁰i>0, якщо ні, (X⁰n+i>0) , тоді його ціна y⁰_i=0, (j=1,…,m);

2) якщо витрати на випуск одиниці j-го виду продукції більші за її ціну, Y⁰_m+j>0, то ця продукція не випускається, X⁰_j=0, якщо Y⁰_m+j=0, тоді випуск j-го виду продукції рентабельний і X⁰_j>0, (j=1,…,n).

З огляду на вищесказане і відповідність змінних, знайдемо оптимальний план двоїстої задачі за даними симплекс-таблиці з оптимальним планом.

Одержимо =(0;0;4,6;0;43,2;36;28,8)

З симплекс-таблиці з оптимальним планом випливає, що min f = max Z = 36800 грош.од..

З огляду на економічний зміст змінних двоїстих задач проведемо економічний аналіз результатів.

Рентабельний тільки випуск продукції першого виду (y⁰₄=0) у кількості X⁰₁=800од. Випуск інших видів продукції не рентабельний, при випуску один. продукції цих видів збитки складуть, відповідно, 43,2(У⁰₅), 36(У⁰₆), 28,8(У⁰₇) грош. одиниць. Тому X⁰₂=X⁰₃=X⁰₄=0. При такому плані випуску максимальна вартість випущеної продукції складе 36800 грош.од..При цьому верстатні ресурси цілком витратяться, їхній залишок X⁰₇=0, вони дефіцитні, їхня ціна за один. складе В⁰₃=4,6 грош.од..Трудові та матеріальні ресурси витрачаються не цілком, вони не дефіцитні. Тому їхня ціна за одиницю. У⁰₁=У⁰₂=0, залишки, відповідно, X⁰₅=600 і X⁰₆=3400 од.

З огляду на вищевикладене, для збільшення сумарної вартості випущеної продукції необхідно збільшувати запаси дефіцитного ресурсу–верстатного.

З [2;3;5] випливає, що

.

Тому збільшення запасу верстатного ресурсу b₃ на один. призведе до збільшення максимальної сумарної вартості випущеної продукції на В⁰₃ =

4,6 грош. од..

3) досліджуємо допустимі межі зміни дефіцитного ресурсу, усередині яких змінні, що входять в оптимальний базис, не змінюються, тобто не змінюється асортимент продукції, що випускається, а змінюється тільки її обсяг залежно від збільшення чи зменшення ресурсу на ∆b. Якщо дефіцитним є i-й ресурс, то, з огляду на лінійність матричних перетворень, можна показати [2;3;5], що новий оптимальний план при зміні i-го ресурсу на ∆b_i буде

(27)

причому

(28)

З (27) і (28) знайдемо ∆b₃, m=4

Тоді b₃ + ∆b₃ буде змінюватися

8000-8000≤b₃≤8000+2000

0≤b₃≤10000

Таким чином, якщо ринок не насичений продукцією першого виду і є конкуренти, підприємству доцільно зменшити запаси трудових і матеріальних ресурсів на 600 і 3400 од., відповідно, і за рахунок цих засобів закупити 2000 од. верстатних ресурсів. Це призведе до збільшення випуску продукції першого виду до X⁰₁ = 800+0,1·2000 = 1000 од. і вартості випущеної продукції до 46·1000 = 46000 грош. од., тобто на 4,6·2000 = 9200 грош. од..

Якщо на ринку немає конкурентів з реалізації продукції першого виду, тобто підприємство монополіст, то збільшення вартості продукції можна досягти іншим шляхом– за рахунок збільшення її ціни. Досліджуємо допустимі межі її зміни ∆C. При цьому будемо використовувати оптимальне розв´язання двоїстої задачі В₀, що знаходиться в оцінному рядку останньої таблиці. Формули, аналогічні (27), (28) мають вигляд

причому

де - вектор – рядок останньої симплекс-таблиці, який відповідає виду продукції, що випускається.

У нашій таблиці це третій рядок. Тоді

∆С₁≥0 ∆С₁≥0

43,2+1,2∆С₁≥0 ∆С₁≥-36

36+∆С₁≥0 => ∆С₁≥-36 => ∆С₁≥0

28,8+0,8∆С₁≥0 ∆С₁≥-36

4,6+0,1∆С₁≥0 ∆С₁≥-46

Тоді 46≤C₁<∞

Одержали, що теоретично ціну на продукцію першого виду можна збільшувати необмежено.

4) проаналізуємо доцільність розширення асортименту за рахунок випуску продукції П-5. Для цього порахуємо для отриманих оптимальних цін на ресурси їхні сумарні витрати на одиницю П-5. Одержимо 5·У⁰₁+6·У⁰₂+9·У⁰₃=5·0 + 6·0 + 9·4,6 = 41,4 грош. од. оскільки витрати менші за заплановану ціну один. продукції (41,4 < 50), то випуск продукції П-5 рентабельний і прибуток від випуску одиниці П-5 складе 8,6 грош. од.

Завдання 3 Розв´язання транспортної задачі

Є три постачальники і чотири споживачі однорідного продукту. Потужності постачальників і попити споживачів, а також витрати на перевезення одиниці вантажу для кожної пари «постачальник-споживач» зведені в таблицю 11 постачань.

Задача у наступному: знайти об'єми перевезень для кожної пари «постачальник-споживач» так, щоб:

1. потужності всіх постачальників були реалізовані;

2. попити всіх споживачів були задоволені;

3. сумарні витрати на перевезення були мінімальні.

Таблиця 11–Потужності постачальників і попити споживачів, витрати на перевезення одиниці вантажу

		Споживачі				Потужність постачальників ai
		B1	B2	B3	B4
Постачальники	A1	1	2	5	3	60
	A2	1	6	5	2	120
	A3	6	3	7	4	100
Попит bj		20	110	40	110	280

Розв´язок

Поставлено збалансовану транспортну задачу, оскільки сумарний попит дорівнює сумарній потужності постачальників  280.

Для отримання начального опорного плану перевезень скористаємось методом мінімального елемента.

Для покращення будемо використовувати таблицю 12, у правому верхньому кутку якої стоїть тариф відповідного перевезення, а у лівому нижньому кутку – плановий обсяг перевезення.

Знаходимо в таблиці клітинки з найменшим тарифом. Таких клітин дві- (1;1) і (2;1) із тарифом, що дорівнює 1. Порівнюємо максимально можливі постачання для цих клітинок: для клітинки (1;1) x₁₁=min{60,20}=20, для клітинки (2;1) x₂₁=min{120,20}=20. Оскільки їх значення збігаються, то максимально можливе постачання записуємо в будь-яку з них. Наприклад, записуємо постачання, що дорівнює 20 од. у клітинку (2;1). У результаті попит першого споживача задоволений і перший стовпець таблиці постачань випадає

з наступного розгляду, а виробничу потужність для другого рядка зменшуємо на 20 од. Аналогічним способом продовжуємо заповнювати невикреслені

Таблиця 12– Отримання начального опорного плану перевезень

	1		2		3		4		ai
1		1		2		5		3	60
			60
2		1		6		5		2	120 100
	20						100
3		6		3		7		4	100
			50		40		10
bj	20		110		40		110		280

клітинки таблиці. У останній клітинці попит і пропозиція повинні збігтися, оскільки розглядається збалансована задача. Слід зазначити, що в таблиці повинна бути заповнена n+m-1 клітинка перевезень ( де n - число постачальників, m- число споживачів ).

Наприклад, для розглянутої задачі повинно бути заповнено 3+4-1=6 клітин. Остаточно одержуємо початковий опорний план перевезень.

Тепер скористаємося методом потенціалів, усі розрахунки виконаємо у таблиці 13. Для цього кожному стовпцю припишемо потенціал v_j , а кожному рядку - потенціал u_i. Для кожної заповненої клітини складемо лінійне рівняння за правилом u_i+v_j=c_ij, де c_ij - тариф відповідного перевезення. Потім розв’яжемо систему 6-ти рівнянь.

Оскільки в рівняннях буде 7 невідомих (3 потенціали u і 4 потенціали v), то довільний потенціал можна дорівняти до нуля.

Тепер для кожної незаповненої клітинки необхідно знайти оцінку _ij= u_i+v_j-c_ij. Якщо всі оцінки будуть негативними або нульовими, то початковий опорний план є оптимальним.

Таблиця 13– Розрахунки методом потенціалів

		1		2		3		4		ai
		V1=3		V2=3		V3=7		V4=4
1	U1=-1	1	1		2	-1	5	0	3	60
				60
2	U2=-2		1	-5	6	0	5		2	120
		20						100
3	U3=0	-3	6		3		7		4	100
				50		40		10
bj		20		110		40		110

₁₁=-1+3-1=1; ₁₃=-1+7-5=1; ₁₄=-1+4-3=0; ₂₂=-2+3-6=-5; ₂₃=-2+7-5=0; ₃₁=0+3-6= -3. Оцінки ₁₁ і ₁₃ позитивні, отже, отримане початкове опорне розв’язання не оптимальне. З оцінок вибираємо найбільшу– ₁₁, отже, у клітинку (1;1) будемо заносити ненульове перевезення. Заносимо в клітинку (1;1) знак «+» і будуємо ланцюг потенціалів, що може проходити тільки по заповнених клітинках, із чергуванням знаків «+» і «-» і повертається у вихідну незаповнену клітину, таблиця 14.

Cеред клітинок, позначених мінусом, вибираємо ту, що містить найменше перевезення.Це клітинка (3;4) з К=Х₃₄ =10. У подальших обчисленнях ця клітинка буде вважатися незаповненою, тому що далі вміст вибраної клітинки,10, додаємо до вмісту клітинок, що позначені «+», і віднімаємо з клітинок, що позначені «-».У таблиці 15 повинна виявитися, як і раніше, n+m-1

Таблиця 14– Перехід до іньшого опорного плану з використанням ланцюга потенціалів

		1		2		3		4		ai
		V1		V2		V3		V4
1	U1		1		2		5		3	60
		+		- 60
2	U2		1		6		5		2	120
		- 20						+ 1 00
3	U3		6		3		7		4	100
				+ 50		40		- 10
b j		20		110		40		110

заповнена клітинка. Перевіряємо отриманий опорний план на оптимальність.

Таблиця 15– Отриманий опорний план

		1		2		3		4		ai
		V1=2		V2=3		V3=7		V4=3
1	U1=-1		1		2	1	5	-1	3	60
		10		- 50		+
2	U2=-1		1	- 4	6	1	5		2	120
		10						110

Продовження таблиці 15

3	U3=0	-4	6		3		7	-1	4	100
				+ 60		- 40
bj		20		110		40		110

₁₃=1; ₁₄=-1; ₂₂= -4; ₂₃=1; ₃₁= -4; ₃₄= -1.

Тому що є дві клітини (1;3) і (2;3) з позитивними оцінками, то отриманий опорний план, таблиця 15, не оптимальний. Знайдемо новий опорний план з використанням ланцюга потенціалів, таблиця 15.

Оскільки дві позитивні оцінки набувають однакових позитивних значень, ₁₃=₂₃=1, то можна занести ненульове перевезення або в клітинку (1;3), або в клітинку (2;3). Якщо у ланцюг будє включено клітинку (1;3),таблиця 15, то це перевезення буде дорівнювати 40 од.. Таким чіном одержано новий опорний план, таблиця 16.

Таблиця 16– Оптимальний опорний план

		1		2		3		4		ai
		V1=1		V2=2		V3=5		V4=2
1	U1=0		1		2		5	-1	3	60
		10		10		40
2	U2=0		1	-4	6	0	5		2	120
		10						110

Продовження таблиці 16

3	U3=1	-4	6		3	-1	7	-1	4	100
				100
bj		20		110		40		110

Перевіряємо отриманий опорний план на оптимальність.

₁₄= -1; ₂₂= -4; ₂₃= 0; ₃₁= -4; ₃₃= -1; ₃₄= -1.

Оскільки серед оцінок немає позитивних, можна сказати, що отриманий опорний план є оптимальним, але не єдиним (₂₃= 0).

У підсумку підприємствам можна запропонувати наступний план перевезень:

П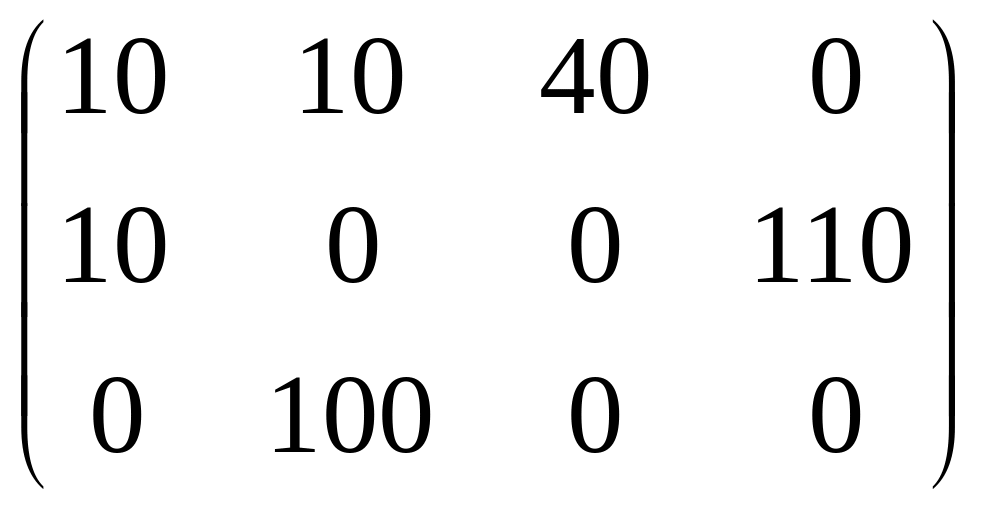 ри такому розподілі перевезень потужності всіх постачальників будуть реалізовані, попит усіх споживачів задоволений, сумарні витрати складуть:

грош. од.

Завдання 4 Розв´язання задачі про призначення

У конструкторському бюро потрібно розробити проект машини, що складається із чотирьох вузлів. До їх розробки можна залучити чотирьох конструкторів. Відомий час, що витрачається кожним конструктором на розробку будь-якого вузла. Потрібно визначити, хто і який вузол машини повинен проектувати, щоб сумарний час проектування всієї машини був мінімальним.

Розв´язок

Нехай необхідно розв’язати задачу про призначення, якщо задана матриця витрат часу на розробку будь-якого вузла кожним конструктором:

.

1. Приведемо матрицю до такого вигляду, щоб у кожному стовпці й кожному рядку знаходився хоча б один нуль. Для цього знайдемо в кожному рядку матриці мінімальний елемент і віднімемо його від усіх елементів відповідного рядка. Аналогічні перетворення виконаємо також з елементами стовпців.

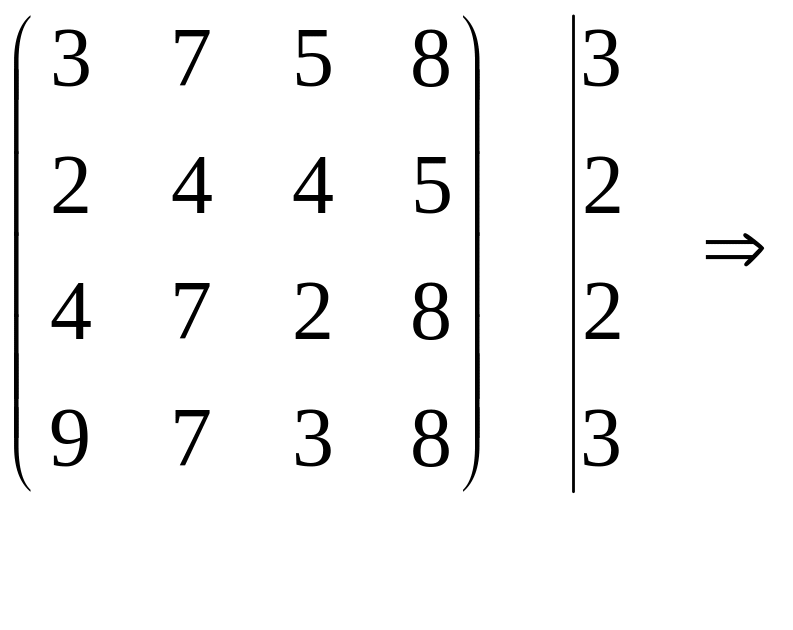
2. Якщо після першого кроку можливий вибір чотирьох незалежних нулів, тоді можна стверджувати, що задача розв’язана. Незалежні нулі для зручності будемо позначати (*). При розставленні позначок найкраще вибирати рядок або стовпець, що містять найменшу кількість нулів. У цьому рядку (стовпці) вибираємо нуль, позначаємо його і викреслюємо інші нулі в рядку чи стовпці, на перетині яких знаходиться вибраний (або незалежний) нуль. Позначки ставимо доти, доки в матриці існують вільні (непозначені або невикреслені) нулі.

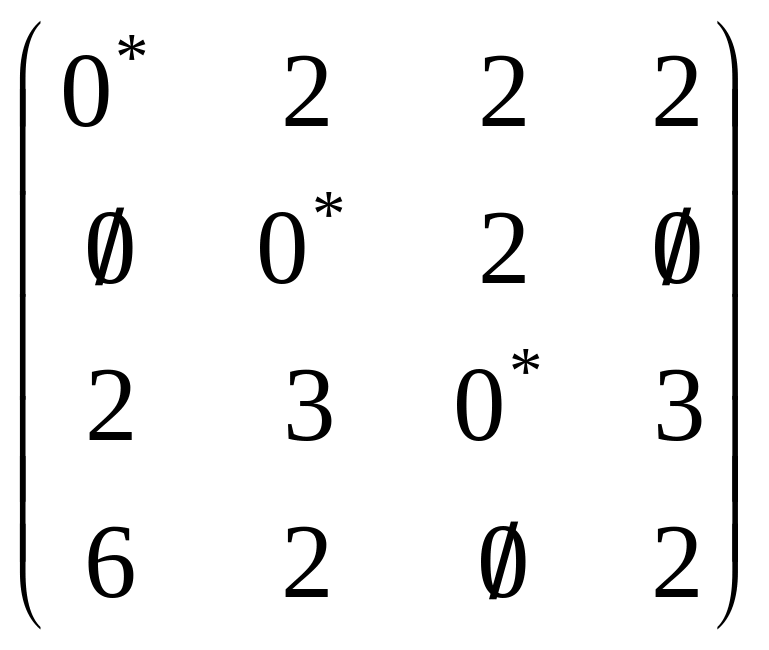
У розглянутому прикладі не вдалося відразу ж одержати оптимальне розв’язання, отже, переходимо до виконання третього кроку.

3. Проведемо мінімальне число горизонтальних і вертикальних ліній, що перетинають, принаймні, один раз усі нулі. Для задач невеликої розмірності візуально легко нанести шукані лінії, для більш складних зручно використати наступний алгоритм:

1. Позначаємо всі рядки, що не містять незалежних нулів.

2. Позначаємо всі стовпці, що містять нуль хоча б в одному позначеному рядку.

3. Позначаємо всі рядки, що містять незалежні нулі в позначених стовпцях.

Кроки 2 і 3 виконуємо доти, доки можливо ставити позначки. Далі викреслюємо непозначені рядки і позначені стовпці.

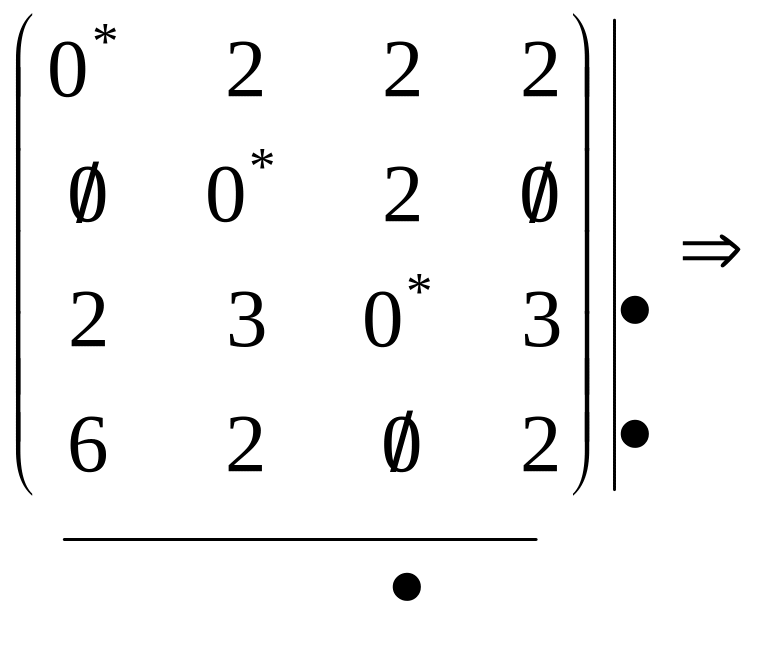
Якщо виявилося, що кількість ліній дорівнює n ,тоді необхідно повернутися на попередній крок (позначки нулів) і знову вибрати незалежні нулі. Такий варіант можливий, якщо при проставлянні позначок 2 або більше нулів у рядку мали «однакове право» бути незалежними.

4. Серед елементів, через які не пройшла жодна з ліній, вибираємо найменший. Віднімаємо це число від усіх елементів, через які не пройшла жодна лінія, і додаємо його до всіх елементів, через які проведені дві лінії.

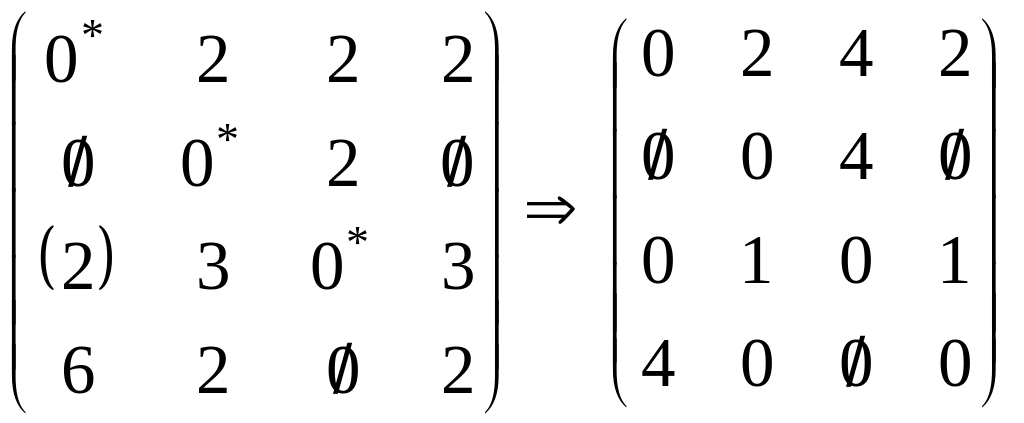
5. П 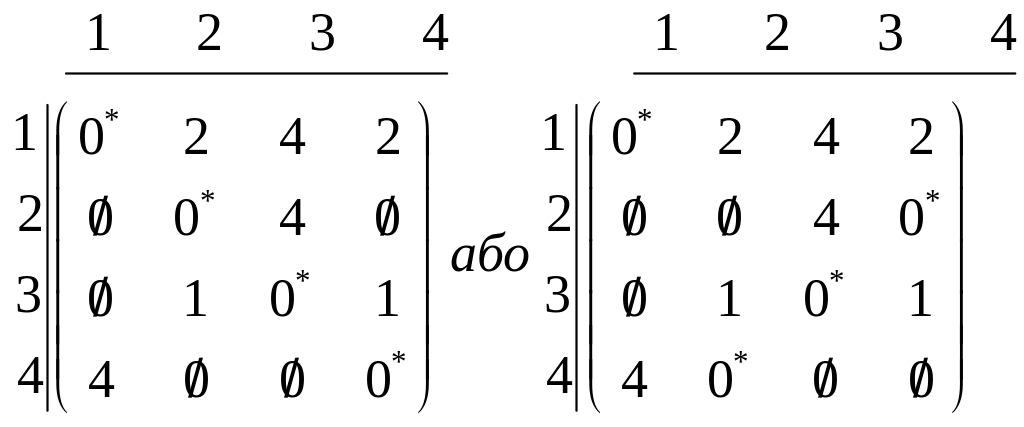овертаємося до кроку вибору незалежних нулів. У розглянутому прикладі одержуємо відразу два оптимальних розв’язання:

1-ше завдання  1-й ресурс;

2-ге завдання  2-й ресурс (або 4-й ресурс);

3-тє завдання  3-й ресурс;

4-те завдання  4-й ресурс (або 2-й ресурс).

У результаті такого призначення система виконає всі завдання за 17 умовних одиниць часу.

Зауваження. У тому випадку, якщо необхідно розв’язати задачу отримання максимального значення функції мети, можна скористатися наступною формулою переходу, що слушна для будь-якої задачі лінійного і нелінійного програмування: min (L) = - max (-L) (тобто елементи матриці С помножити на (-1) ).

Завдання 5 Розв’язати задачу цілочислового програмування

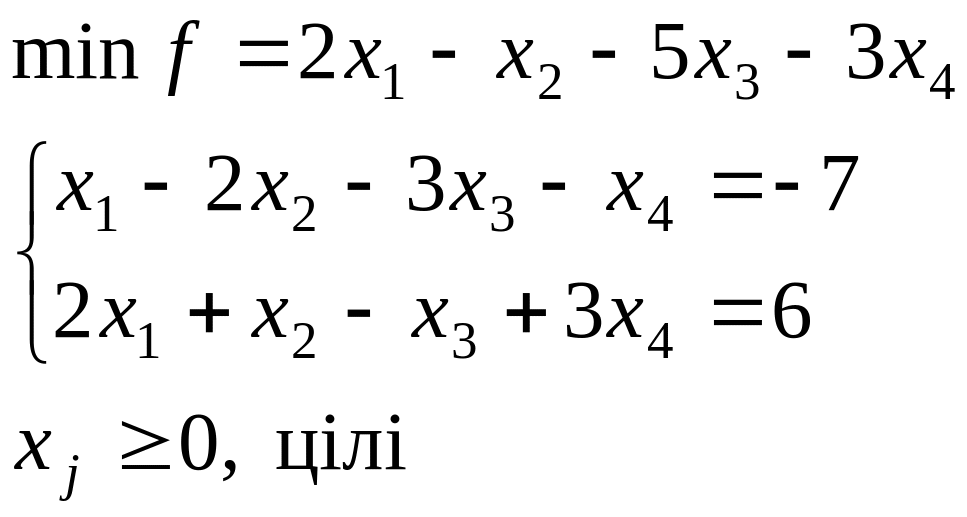
Розв’язання

Зведемо ЗЛП до канонічного вигляду, помноживши перше рівняння на –1.

Оскільки в рівняннях обмежень відсутні базисні змінні, то введемо штучні базисні змінні , і розв’яжемо М-задачу в симплекс-таблиці 17.

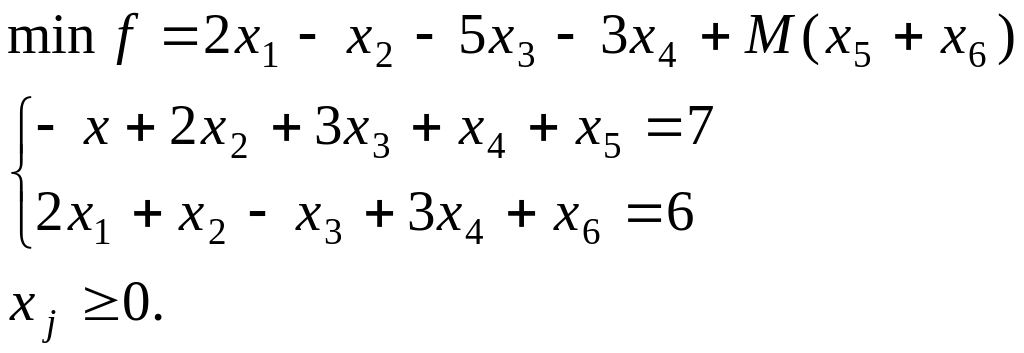
Таблиця 17– Симплекс-таблиця М-задачі

		с	2	-1	-5	-3	М	М
хб	сб	xi	x1	x2	х3	х4	x5	х6	Q
х5	М	7	-1	2	3	1	1	0	7/3
x6	М	6	2	1	-1	3	0	1	6/3
без М		0	-2	1	5	3	0	0	∆'j
с М		13	1	3	2	4	0	0	∆''j
х5	М	5	-5/3	5/3	10/3	0	1	-1/3	1,5
х4	-3	2	2/3	1/3	-1/3	1	0	1/3
без М		-6	-4	0	6	0	0	-1	∆'j
с М		5	-5/3	5/3	10/3	0	0	-4/3	∆''j
x3	-5	1,5	-0,5	0,5	1	0	0,3	-0,1
х4	-3	2,5	0,5	0,5	0	1	0,1	0,3
без М	f	-15	-1	-3	0	0	-1,8	-0,4	∆'j
с М		0	0	0	0	0	-1	-1	∆''j

Оскільки , то отриманий план ЗЛП: не цілочисловий. Застосуємо метод Гоморі і знайдемо розв’язання ЗЦП.

Складемо правильне відсікання

.

Оскільки , то для побудови відсікання можна взяти будь-який рядок, наприклад, другий.

Одержимо

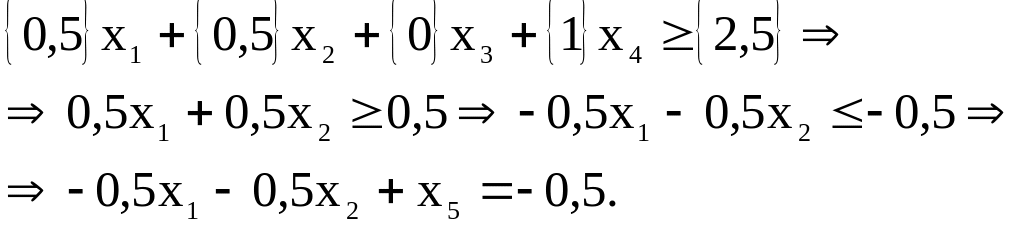
Додамо це обмеження новим рядком до симплекс-таблиці 18.

Оскільки j , то отриманий план: , оптимальний, цілочисловий,

Таблиця 18– Симплекс-таблиця

			2	-1	-5	-3	0
Хб	Сб	Xі	X1	X2	X3	X4	X5	Q
x3	-5	1,5	-0,5	0,5	1	0	0
х4	-3	2,5	0,5	0,5	0	1	0	0,5
х5	0	-0,5	-0,5	-0,5	0	0	1	1
f	=	-1,5	-1	-3	0	0	0	j
x3	-5	2	0	2	1	0	-1
х4	-3	2	0	0	0	1	1
x1	2	1	1	1	0	0	-2
f	=	-14	0	-2	0	0	-2	j

Зауваження. Якщо розв’язувати З.Ц.П. на максимум функції мети f, тоді штучні базисні змінні додаються до функції мети з коефіцієнтами – М.