§2.6. Опуклість кривої і точки перегину

Н ехай функція диференційована на інтервалі . Графік цієї функції називають опуклим угору (Рис. 5) на інтервалі , якщо на цьому інтервалі він розміщений не вище будь-якої своєї дотичної і опуклим униз (Рис. 6), якщо він розміщений не нижче дотичної. Точка називається точкою перегину (Рис. 7) кривої , якщо при переході через цю точку крива змінює напрям опуклості.

Дослідження кривої на опуклість і точки перегину здійснюється за допомогою другої похідної. Якщо для будь-якого х з інтервалу , то крива опукла униз на цьому інтервалі; якщо ж , то крива опукла угору. Критичними точками другого роду функції називаються точки, в яких її друга похідна дорівнює нулю або не існує.

Необхідна умова точки перегину: якщо – точка перегину кривої, то у цій точці друга похідна функції дорівнює нулю або не існує (х₀ – критична точка другого роду).

Достатня умова точки перегину: нехай х₀ – критична точка другого роду функції ; тоді, якщо друга похідна змінює знак при переході через точку х₀, то точка є точкою перегину.

Дослідження графіка функції на опуклість і точки перегину здійснюється за наступною схемою:

1. знаходимо область визначення функції;

2. знаходимо критичні точки другого роду;

3. на числовій прямій відмічаємо всі критичні точки другого роду і точки розриву функції;

4. визначаємо знак другої похідної на кожному із отриманих інтервалів області визначення функції;

5. використовуючи відповідні умови, визначаємо інтервали опуклості і точки перегину кривої.

Приклад 1. Знайти інтервали опуклості і точки перегину кривих:

а) ; б) ; в) .

Розв’язання. а) Функція визначена для всіх , тобто ; Знаходимо критичні точки другого роду:

, ;

, , ;

Так як друга похідна визначена на всій числові прямій, то інших критичних точок другого роду не існує. Будуємо числову пряму; відмічаємо на ній знайдені точки (точок розриву немає); визначаємо знак другої похідної і напрям опуклості на отриманих інтервалах; знаходимо точки перегину (Рис. 8).

Маємо: крива опукла униз на інтервалах і ; опукла угору на ; і – точки перегину.

б) Аналогічно попередньому дістаємо:

; ;

.

Критичних точок другого роду немає, так як друга похідна відмінна від 0 і визначена на всій області визначення функції (точка не входить в область визначення). Враховуючи, що на інтервалі , робимо висновок, що графік функції опуклий униз у всій області визначення. Точок перегину немає.

в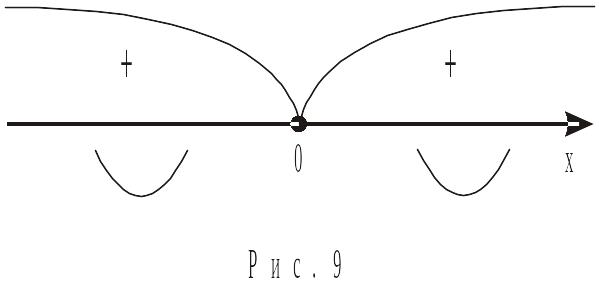 ) Маємо: ; ; .

Так як в точці друга похідна не існує і функція визначена, то (0;0) – критична точка другого роду. На обох отриманих інтервалах і крива опукла униз. Точок перегину немає (рис.9).

§2.7. Повне дослідження функції, побудова графіка

Наведемо схему повного дослідження функції і побудови її графіка:

1. знаходимо область визначення функції;

2. досліджуємо функцію на парність, непарність і періодичність;

3. знаходимо точки перетину кривої з осями координат і інтервали знакосталості;

4. визначаємо асимптоти кривої і характер точок розриву;

5. знаходимо проміжки зростання, спадання і екстремуми функції;

6. досліджуємо графік функції на опуклість і точки перегину;

7. будуємо графік функції.

Розглянемо більш детально наведену схему на конкретних прикладах.

Приклад 1. Провести повне дослідження функцій і побудувати їхні графіки:

а) ; б) .

Розв’язання. а) Враховуючи, що знаменник дробу дорівнює нулю при , знаходимо область визначення функції

.

Нагадаємо, що функція називається парною, якщо область її визначення симетрична відносно нуля і якщо для будь-якого х виконується рівність ; якщо ж , то функція називається непарною. Графік парної функції симетричний відносно осі Оу, а графік непарної – відносно початку координат. У нашому випадку область визначення симетрична відносно нуля і

.

Функція непарна (побудований графік повинен бути симетричним відносно початку координат).

Легко бачити, що функція неперіодична.

Знайдемо точки перетину графіка функції з віссю Ох (у цих точках ): , , ; (0;0) – точка перетину з віссю Ох.

Визначаємо точки перетину графіка функції з віссю Оу (у цих точках ): ; (0;0) – точка перетину з віссю Оу.

З найдемо інтервали знакосталості. Для цього на числовій прямій відмічаємо точки перетину кривої з віссю Ох і точки розриву, а потім визначаємо знак функції на кожному з одержаних проміжків області визначення функції (рис. 10). Як бачимо функція додатна на інтервалах і , від’ємна на і .

Шукаємо похилі і горизонтальні асимптоти (див. §2.2):

;

;

– похила асимптота.

Так як

, ,

, ,

то прямі і є вертикальними асимптотами ( – точки розриву другого роду).

Досліджуємо функцію на інтервали зростання, спадання і точки екстремуми (див. §2.5.):

;

, , , , .

Функція зростає на інтервалах і . Функція спадає на інтервалах , , і . Точка – точка максимуму ; – точка мінімуму .

Досліджуємо функцію на опуклість і точки перегину (див. §2.6):

;

, , , .

Ф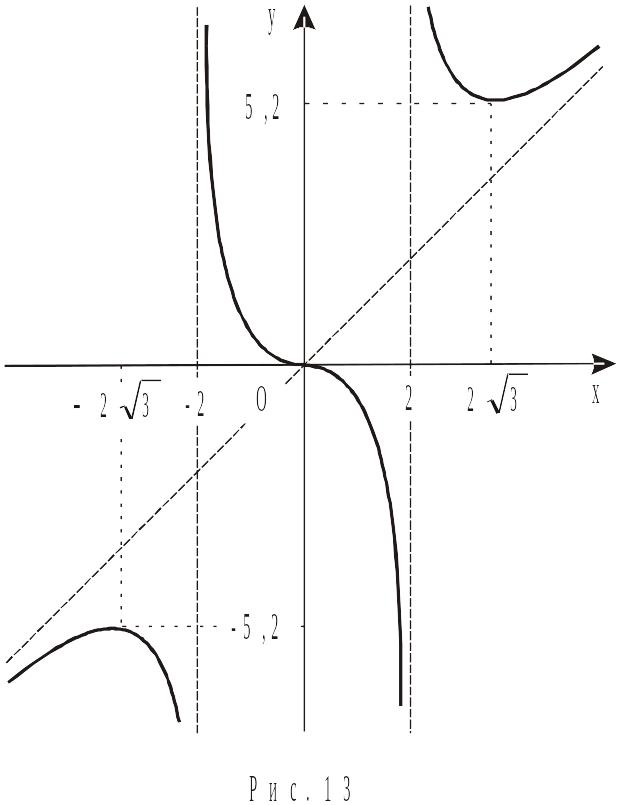 ункція опукла угору на інтервалах і ; опукла униз на інтервалах і ; (0; 0) – точка перегину.

Будуємо графік функції (Рис. 13).

б) Областю визначення функції є інтервал .

Так як область визначення не симетрична відносно нуля, то функція не парна і не непарна. Функція неперіодична.

Знаходимо точки перетину кривої з віссю Ох:

; (1;0) – точка перетину з віссю Ох.

В ісь Оу графік функції не перетинає .

Інтервали знакосталості (рис.14): на інтервалі (0;1) функція від’ємна, на – додатна.

Знаходимо похилі і горизонтальні асимптоти:

;

;

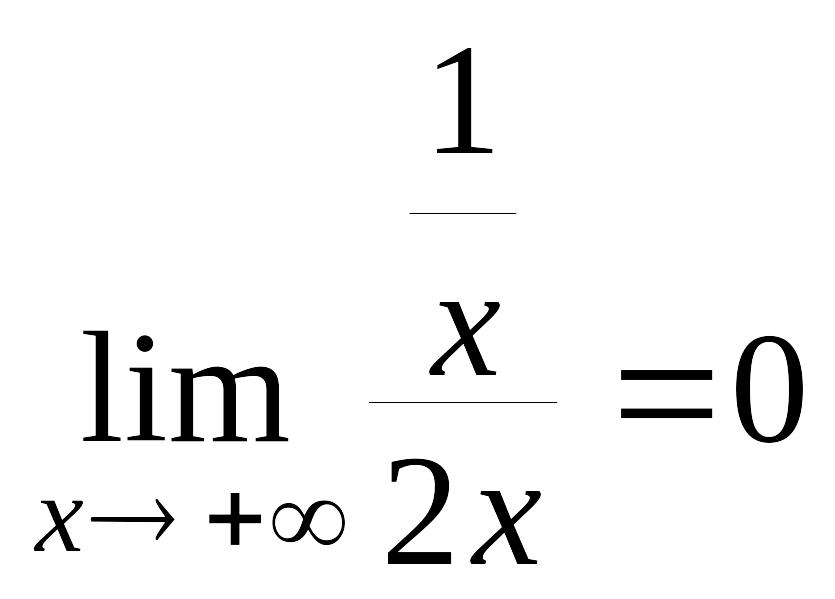(вісь Ох) – горизонтальна асимптота.

Так як , то – вертикальна асимптота.

Досліджуємо функцію на монотонність і точки екстремуму:

; , , .

Ф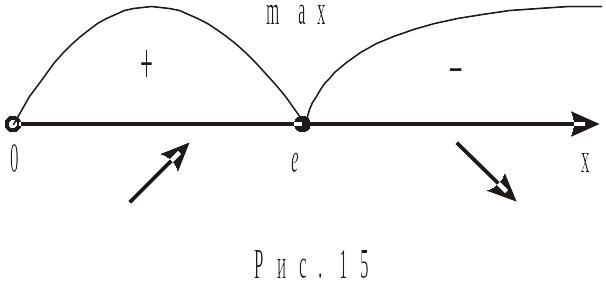 ункція зростає на інтервалі , спадає на інтервалі – точка максимуму .

Досліджуємо графік функції на опуклість і точки перегину:

;

, , .

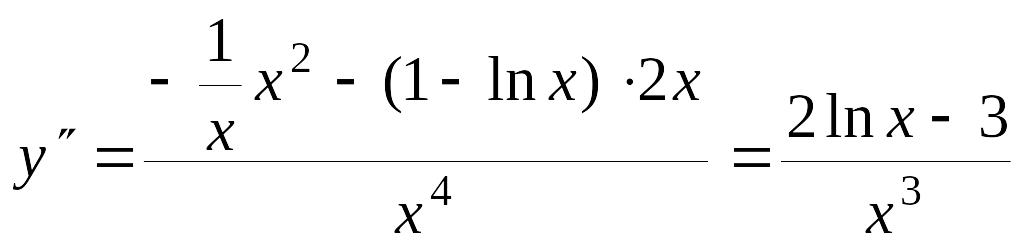На інтервалі крива опукла угору, на інтервалі – униз; – точка перегину.

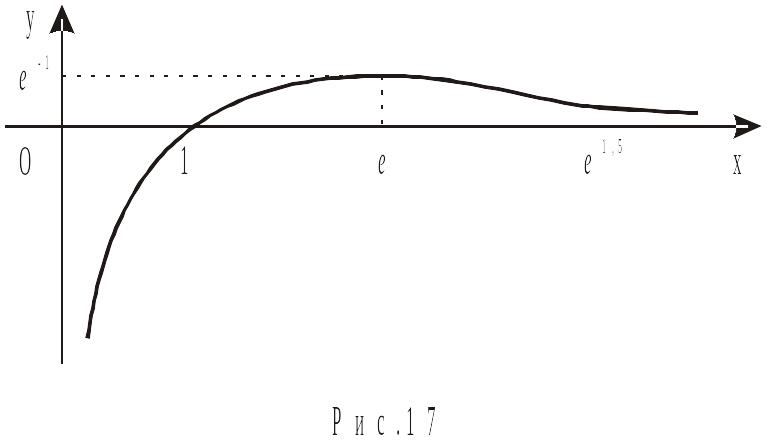
Будуємо графік (рис. 17).

Розділ 3. Невизначений інтеграл