§ 4.4. Довжина дуги кривої.

Довжина дуги кривої обчислюється за формулою

. (4.1)

Якщо крива задана параметричними рівняннями , , то формула (3.1) перетворюється до вигляду

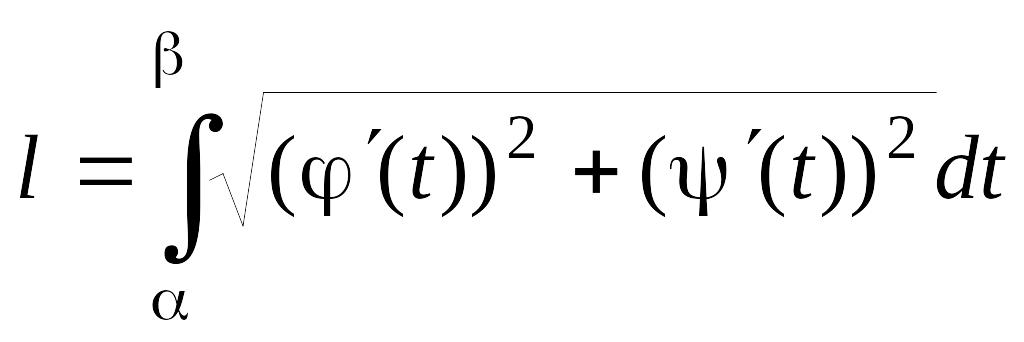. (4.2)

У випадку полярних координатах, коли лінія задана рівнянням , , довжина дуги визначається формулою

. (4.3)

Приклад 1. Обчислити довжину дуги параболи від до .

Розв’язання. Застосуємо формулу (4.1). Знайдемо спочатку підінтегральну функцію:

.

Обчислюємо довжину (знаходження первісної див. § 3.2, прикл. 2б):

.

Якщо крива задана параметричними рівняннями , , то формула (4.1) перетворюється до вигляду

. (4.2)

Довжина дуги просторової кривої , , обчислюється за формулою

. (4.3)

Приклад 2. Знайти довжину дуги астероїди від до .

Розв’язання. Лінія задана параметричними рівняннями, тому скористаємося формулою (4.2). Маємо:

;

.

У випадку полярних координатах, коли лінія задана рівнянням , , довжина дуги визначається формулою

. (4.4)

Приклад 3. Обчислити довжину дуги кривої , .

Розв’язання. Крива задана у полярній системі координат. Застосуємо формулу (4.4):

.

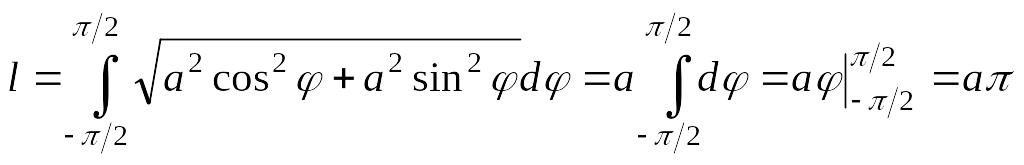§ 4.5. Обчислення об’єму тіла обертання і площі поверхні обертання

Р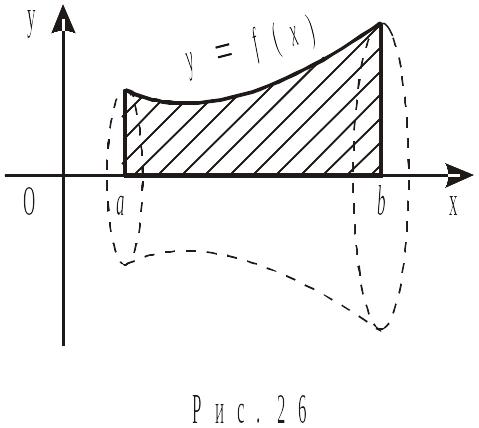 озглянемо криволінійну трапецію, обмежену лінією віссю Ох і двома вертикальними прямими (рис.26). Обертаючи цю фігуру навколо осі Ох, одержимо тіло у просторі. Об’єм отриманого тіла обертання і площа поверхні обертання обчислюються відповідно за формулами:

, (5.1)

. (5.2)

Якщо крива, яка обмежує криволінійну трапецію зверху, задана параметричними рівняннями , , , то

, (5.3)

. (5.4)

Межі інтегрування у формулі (5.3) визначаються рівностями і (можливі варіанти або ).

Приклад 1. Плоска фігура, яка обмежена лініями , , обертається навколо осі Ох. Обчислити: а) об’єм тіла обертання; б) площу поверхні обертання.

Розв’язання. а) Побудувавши фігуру (рис.20) і застосувавши формулу (5.1), отримуємо

.

б) Використовуючи формулу (5.2), дістаємо

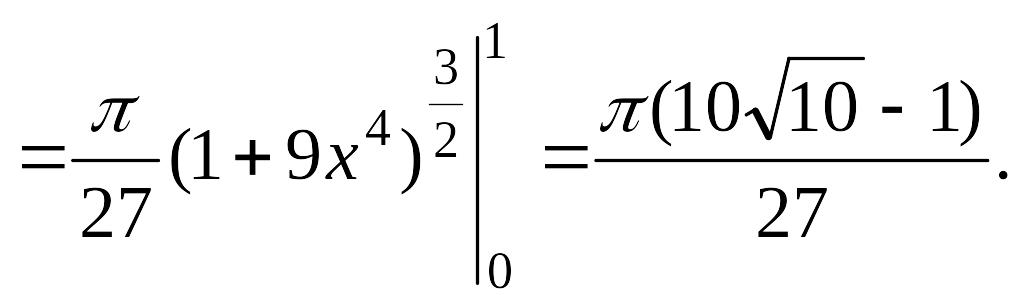
§ 4.6. Обчислення статичних моментів, моментів інерції та координат центра ваги

При розв’язанні багатьох задач механіки та фізики використовуються такі поняття як статичні моменти, моменти інерції та центр ваги. Наведемо далі методи обчислення вказаних величин для криволінійної трапеції та дуги плоскої кривої (розглядаються однорідні тіла з густиною ).

Нехай задана дуга плоскої кривої , яка обмежена прямими і . Статичні моменти дуги відносно координатних осей (позначаються через М_х, М_у), моменти інерції дуги (позначаються через І_х, І_у) та координати центра ваги (позначаються через ) обчислюються за формулами:

, (6.1)

, (6.2)

, (6.3)

де l – довжина дуги.

Приклад 1. Знайти статичний момент дуги кривої відносно осі Ох.

Розв’язання. Застосовуємо першу з формул (6.1):

;

.

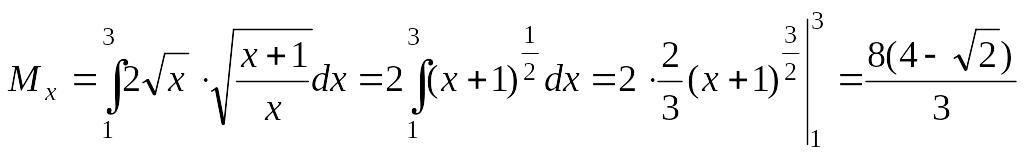Якщо дуга задана параметричними рівняннями , то відповідні формули приймають вигляд:

, (6.4)

, (6.5)

. (6.6)

Приклад 2. Знайти момент інерції дуги кривої відносно осі Оу.

Розв’язання. Використовуємо другу з формул (6.5):

;

;

.

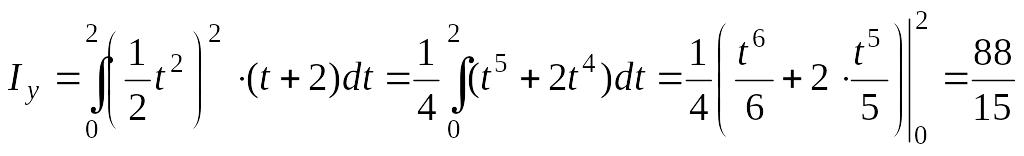Розглянемо тепер криволінійну трапецію, яка обмежена прямими кривою і віссю Ох (рис. 19). Статичні моменти, моменти інерції та координати центра ваги вказаної фігури обчислюються за формулами:

, (6.7)

, (6.8)

, (6.9)

де S – площа фігури.

Приклад 3. Знайти координати центра ваги плоскої фігури, яка обмежена дугою параболи та віссю Ох.

Розв’язання. Так як фігура симетрична відносно прямої (рис. 27), то . Використовуючи формули (6.9), отримуємо:

;

.

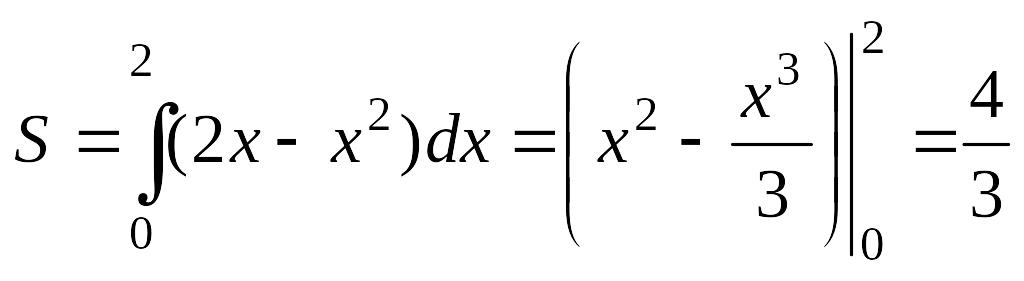Якщо дуга, яка обмежує криволінійну трапецію зверху, задана параметричними рівняннями , то маємо:

, (6.10)

, (6.11)

. (6.12)

Межі інтегрування у формулах (6.10) – (6.12) визначаються рівностями , тобто відповідає крайнім лівим точкам криволінійної трапеції, а – крайнім правим.

Приклад 4. Знайти момент інерції І_у плоскої фігури, яка обмежена дугою кола прямими і віссю Ох.

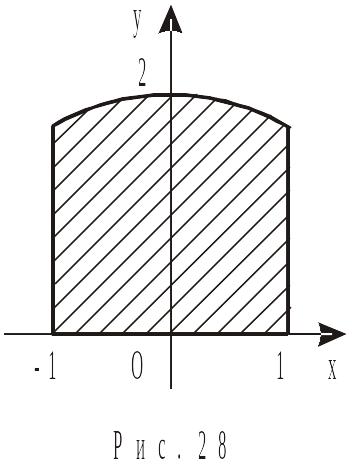Розв’язання. Оскільки крива, яка обмежує криволінійну трапецію зверху (рис. 28) задана параметричними рівняннями, то використовуємо другу з формул (6.11). Знайдемо спочатку межі інтегрування:

.

Визначаємо момент інерції:

.
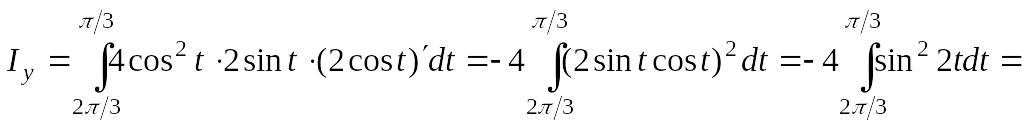
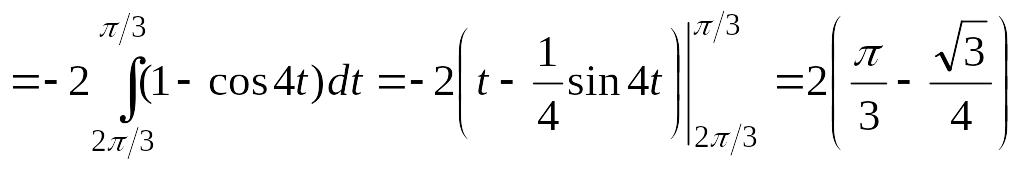