§1.5. Поняття про похідні вищих порядків

Нехай функція диференційована в точці х, тобто у цій точці існує похідна . Якщо для функції f(x) у точці х існує похідна від похідної , то вона називається похідною другого порядку або другою похідною. Похідною третього порядку називається похідна від похідної другого порядку і т. д. Для вказаних похідних вищих порядків прийняті позначення , , …, або , , …, .

Приклад 1. Знайти похідні другого порядку для наступних функцій:

а) ; б) .

Розв‘язання. У відповідності з означенням другої похідної можемо записати:

а) , ;

б) , .

Якщо функцію задано параметрично , , то похідна другого порядку від у по х обчислюється за формулою:

(5.1)

або

. (5.2)

Приклад 2. Знайти похідні другого порядку від функцій заданих параметрично:

а) б)

Розв’язання. а) Користуючись формулою (5.1), отримуємо:

, .

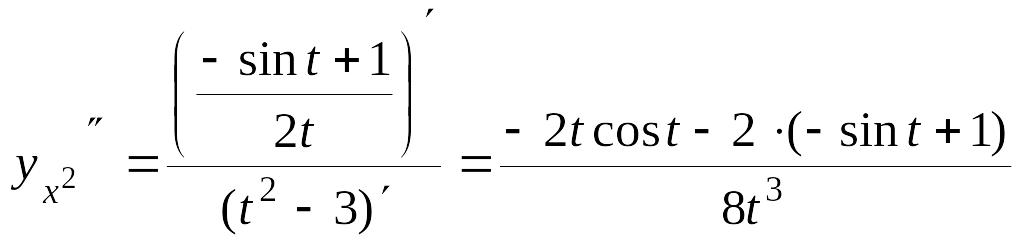б) Застосовуючи формулу (5.2), дістаємо:

, , ,

; .

_{Розділ 2. Застосування похідної і диференціала. Дослідження функції}

§ 2.1. Знаходження границі за допомогою похідної. Правило Лопіталя

Правило Лопіталя застосовується для обчислення границь. Сформулюємо його суть. Нехай функції і диференційовані в околі точки і нехай в цій точці вони одночасно нескінченно малі або нескінченно великі, тобто

і або і .

Тоді, якщо існує границя , то існує також границя , причому:

. (1.1)

Очевидно, що правило Лопіталя використовується для розкриття невизначеностей виду і .

_{Приклад 1. Обчислити границі:}

а) ; б) ; в) .

Розв’язання. Застосовуючи правило Лопіталя, дістаємо:

а) = = = = ;

б) = = = .

в) При обчисленні цієї границі правило Лопіталя необхідно застосувати два рази (у загальному випадку при виконанні потрібних умов це можна робити декілька разів).

= = = =

= = =

= = =1.

Правило Лопіталя використовується також для розкриття невизначеностей типу , , , і . У всіх вказаних випадках можна зробити перетворення, після яких дістанемо невизначеність виду або _.

Приклад 2. Обчислити границі:

а) ; б) ; в) .

Розв’язання. У наведених нижче розв’язках спочатку за допомогою елементарних перетворень зводимо задану границю до невизначеності або , а потім застосовуємо правило Лопіталя.

а) = = = = .

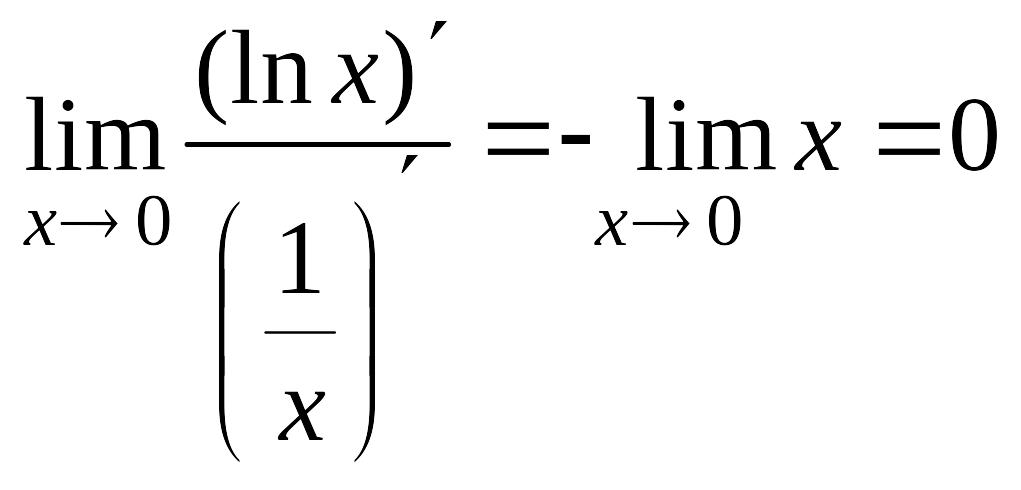б) = = =

=

= .

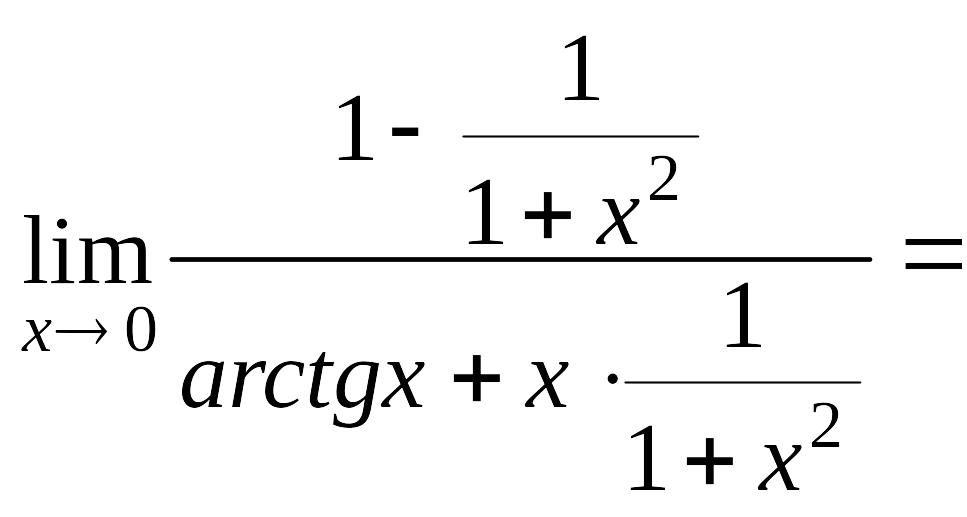
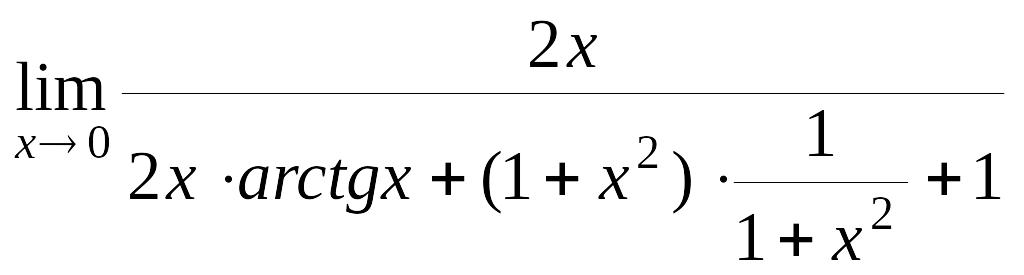
в) = = .

Так як

,

то

, .

При розкритті невизначеностей , і зручно використовувати тотожність

. (1.2)

Формула (1.2) здобута за допомогою основної логарифмічної тотожності.

Приклад 3. Обчислити границю .

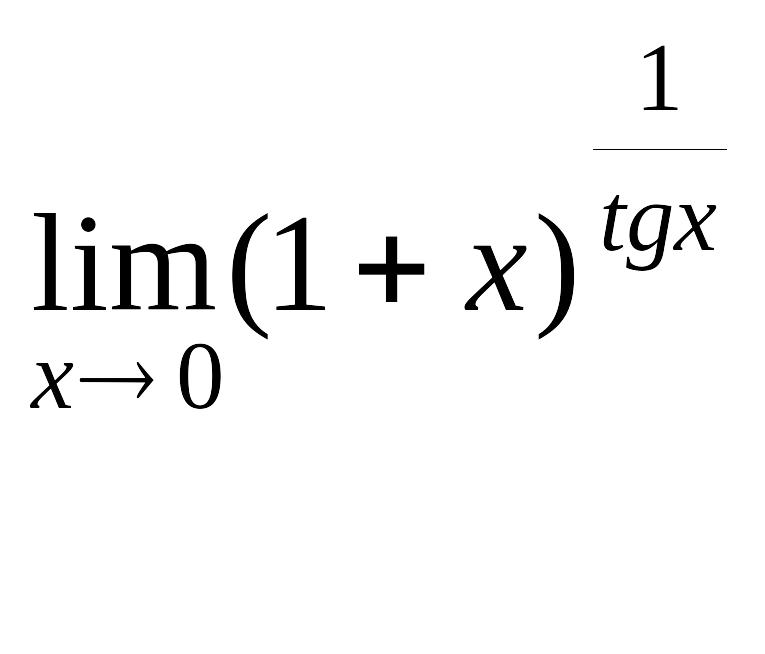Розв'язання. Застосовуючи формулу (1.2), маємо

= = = .

Знайдемо границю показника:

.

Дістаємо кінцевий результат:

.

§ 2.2. Асимптоти кривої

Нехай задана функція . Якщо існує пряма, така, що відстань від точки кривої до цієї прямої прямує до нуля при нескінченному віддалені точки М від початку системи координат, то ця пряма називається асимптотою кривої (або графіка функції) .

Розрізняють три види асимптот: похилі, горизонтальні і вертикальні. Похилі і горизонтальні асимптоти шукають у формі , де

. (2.1)

Якщо хоча б одна з границь формул (2.1) не існує (дорівнює нескінченності), то крива не має вказаних асимптот. У випадку, коли обидві границі існують і , крива має горизонтальну асимптоту . Параметри k i b можуть бути різними при і при . У цьому випадку крива має дві похилі асимптоти.

Пряма є вертикальною асимптотою, якщо

. (2.2)

Границя у формулі (2.2) може бути односторонньою. Якщо функція визначена на усій числовій прямій, то її графік не має вертикальних асимптот.

Приклад 1. Знайти асимптоти кривих:

а) ; б) ; в) ;

г) ; д) .

Розв’язання. Для всіх кривих спочатку за допомогою формул (2.1) визначаємо похилі і горизонтальні асимптоти, а потім, використовуючи формулу (2.2) – вертикальні.

а) = =1;

= =

= = =2.

Отже пряма є похилою асимптотою.

Вертикальних асимптот немає, так як функція визначена на інтервалі (немає точок, в яких виконується умова (2.2)).

б) .

Пряма – горизонтальна асимптота.

Вертикальних асимптот немає.

в) Для цієї кривої границі формул (2.1) потрібно розглядати окремо при і при (у попередніх випадках вони співпадали).

;

.

Пряма – похила асимптота (ліва).

;

.

Пряма – похила асимптота (права).

Вертикальних асимптот немає.

г) Так як , то похилих і горизонтальних асимптот немає. Оскільки , то пряма є вертикальною асимптотою (точка є точкою розриву другого роду).

д) Відзначимо, що дана функція визначена на інтервалі , що потрібно враховувати при знаходженні відповідних границь. Так як

,

то похилих і горизонтальних асимптот немає. Оскільки

= ,

то пряма є вертикальною асимптотою.