
- •Кіровоградський національний технічний університет факультет проектування і експлуатації машин кафедра вищої математики та фізики
- •Кіровоград
- •Організація навчального процесу за кредитно-модульною системою
- •§ 1.1. Поняття та властивості похідної
- •§1.2. Похідна складної функції і функції, заданої параметрично
- •§1.3. Диференціювання неявно заданих функцій. Логарифмічне диференціювання
- •§1.4. Диференціал функції. Наближені обчислення за допомогою диференціала
- •§1.5. Поняття про похідні вищих порядків
- •§ 2.1. Знаходження границі за допомогою похідної. Правило Лопіталя
- •§ 2.2. Асимптоти кривої
- •§ 2.3. Рівняння дотичної і нормалі до графіка функції
- •§ 2.4. Обчислення найбільшого і найменшого значень функції на відрізку
- •§2.5. Дослідження функції на зростання, спадання і точки екстремуму
- •§2.6. Опуклість кривої і точки перегину
- •§2.7. Повне дослідження функції, побудова графіка
- •§3.1. Поняття невизначеного інтеграла. Найпростіші прийоми інтегрування
- •§3.2. Методи інтегрування
- •§3.3. Інтегрування деяких виразів, що містять квадратний тричлен.
- •§3.4. Інтегрування найпростіших дробів
- •§3.5. Інтегрування дробово-раціональних функцій
- •§3.6. Інтегрування тригонометричних функцій.
- •§3.7. Інтегрування ірраціональних функцій
- •§ 4.1. Означення та основні властивості визначеного інтеграла.
- •§ 4.2. Обчислення визначеного інтеграла.
- •§ 4.3. Площа плоскої фігури.
- •§ 4.4. Довжина дуги кривої.
- •§ 4.5. Обчислення об’єму тіла обертання і площі поверхні обертання
- •§ 4.6. Обчислення статичних моментів, моментів інерції та координат центра ваги
- •§ 4.7. Обчислення роботи та деякі задачі механіки рідин
- •§ 4.8. Невласні інтеграли
- •§ 4.9. Наближені обчислення визначеного інтеграла
- •Індивідуальні завдання для самостійної роботи Диференціальне числення функції однієї змінної
- •Інтегральне числення
- •Рекомендована література
Індивідуальні завдання для самостійної роботи Диференціальне числення функції однієї змінної
Завдання 1. Знайти похідні функцій, використовуючи означення похідної.
а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а) ; б)
 .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б)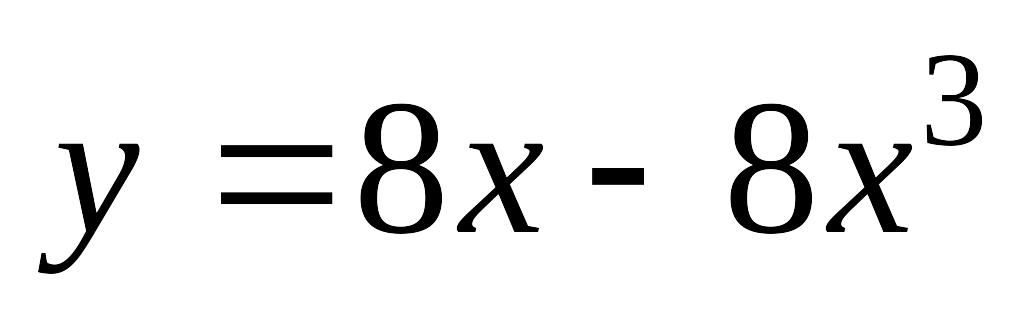 .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б)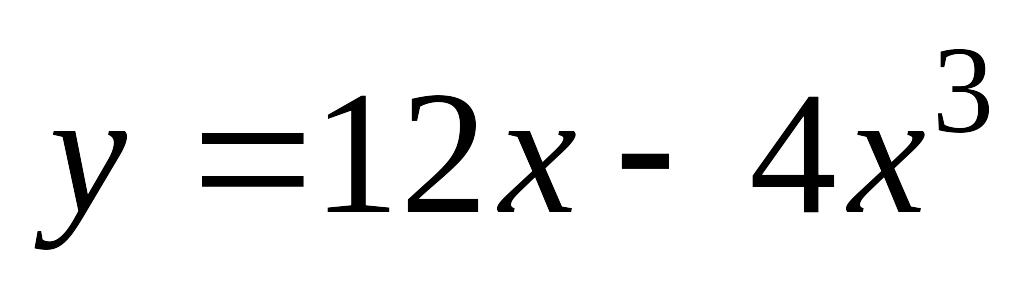 .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б)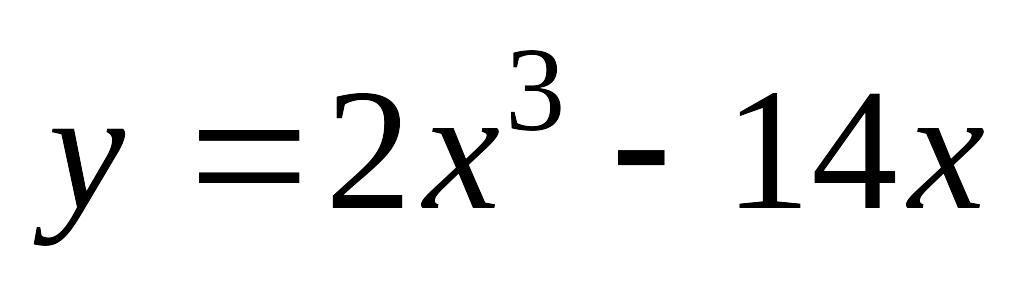 .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.
Завдання 2. Знайти похідні першого порядку.
1. а)![]() ; б)
; б)![]() ;
;
в)![]() ; г)
; г)![]() .
.
2. а)![]() ; б)
; б)![]() ;
;
в)![]() ; г)
; г)![]() .
.
3. а)![]() ; б)
; б)![]() ;
;
в)![]() ; г)
; г)![]() .
.
4. а)![]() ; б)
; б)![]() ;
;
в)![]() ; г)
; г)![]() .
.
5. а)![]() ; б)
; б)![]() ;
;
в)![]() ; г)
; г)![]() .
.
6. а)![]() ; б)
; б)![]() ;
;
в)![]() ; г)
; г)![]() .
.
7. а)
![]() ; б)
; б)![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
8. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
9. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
10. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
11. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
12. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
13. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
14. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
15. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
16. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
17. а)![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
18. а)![]() ; б)
; б)
![]() ;
;
в)![]() ; г)
; г)
![]() .
.
19. а)![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
20. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
21. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
22. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
23. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
24. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
25. а)
![]() ; б)
; б)
 ;
;
в)
![]() ; г)
; г)
![]() .
.
26. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
27. a)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
28. a)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
29. a)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
30. a)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
Завдання 3. Знайти похідні першого порядку від функцій, заданих неявно і в параметричній формі.
а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б)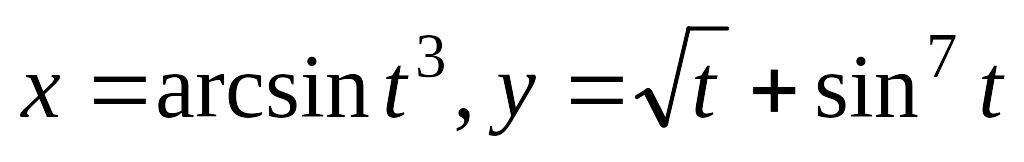 .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б)
а)
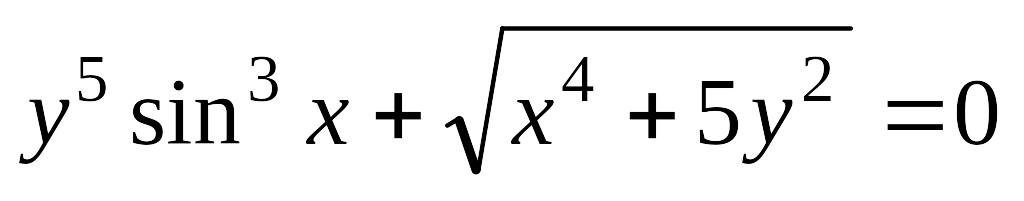 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
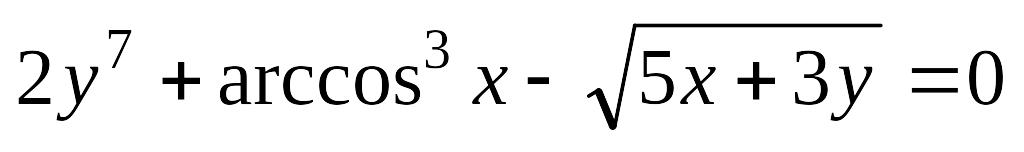 ; б)
; б) .
.а)
 ; б)
; б)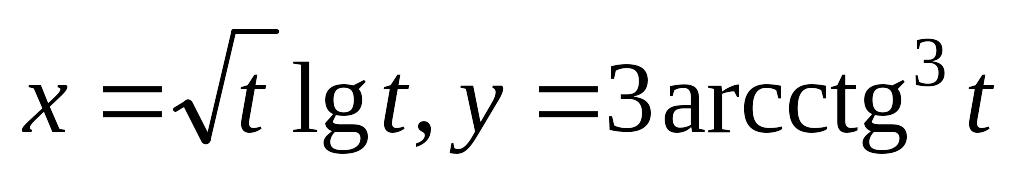 .
.а)
 ; б)
; б) .
.а)
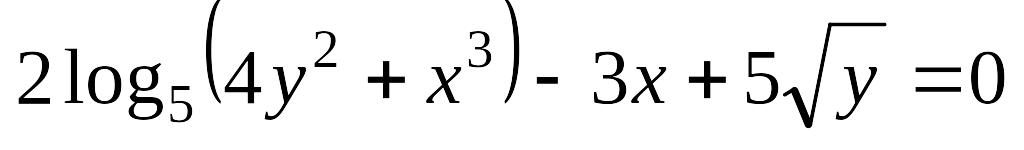 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ;б)
;б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б)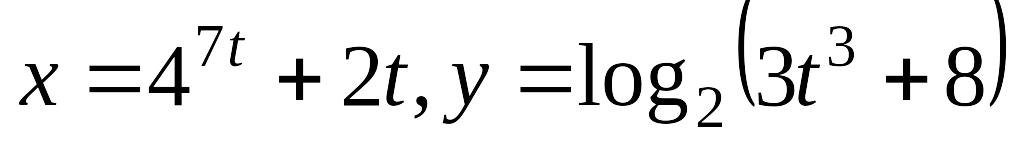 .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
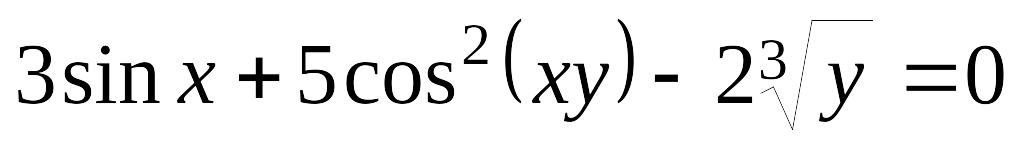 ; б)
; б) .
.
30. а)![]() ; б)
; б)![]() .
.
Завдання 4. Знайти похідні.
a)
 ; б)
; б) .
.а)
 ; б)
; б) .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
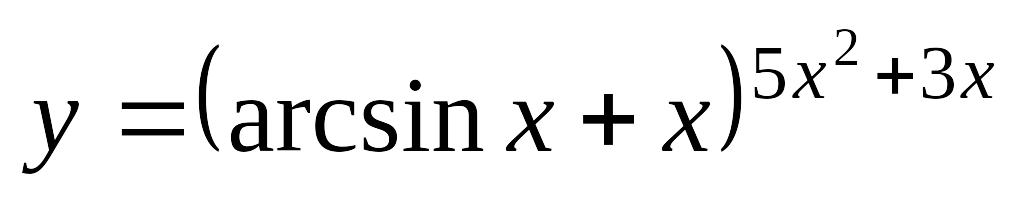 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
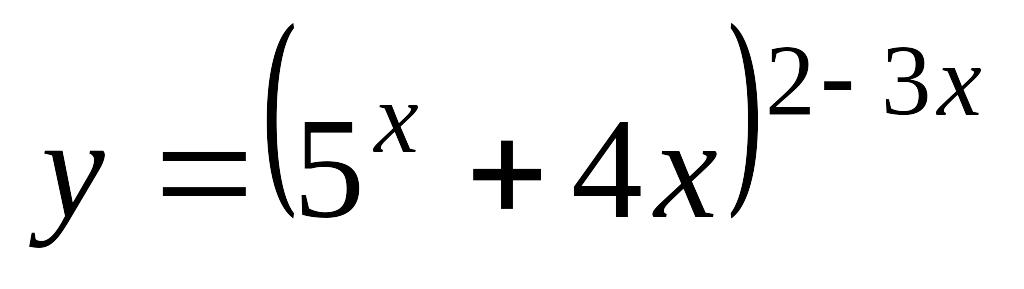 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
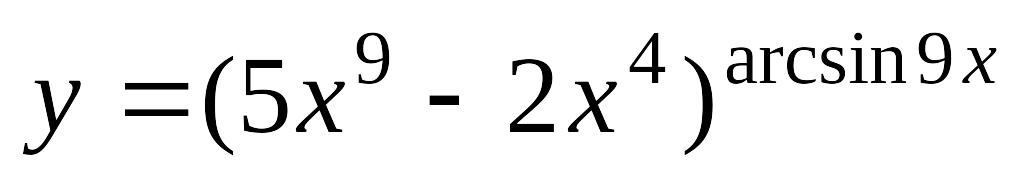 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
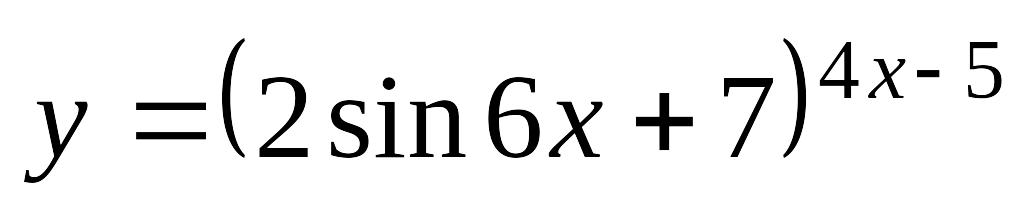 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
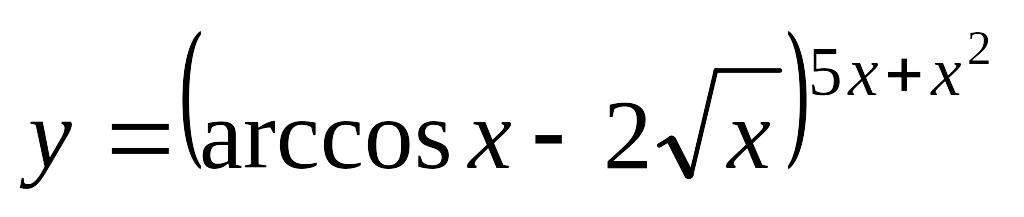 .
.а)
 ; б)
; б)
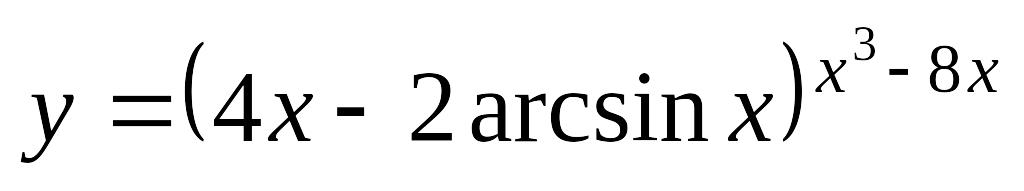 ;
;а)
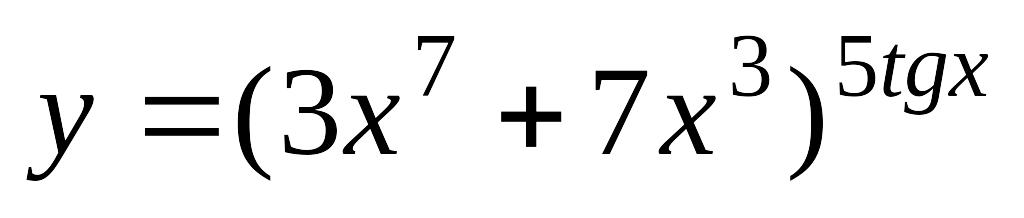 ; б)
; б)
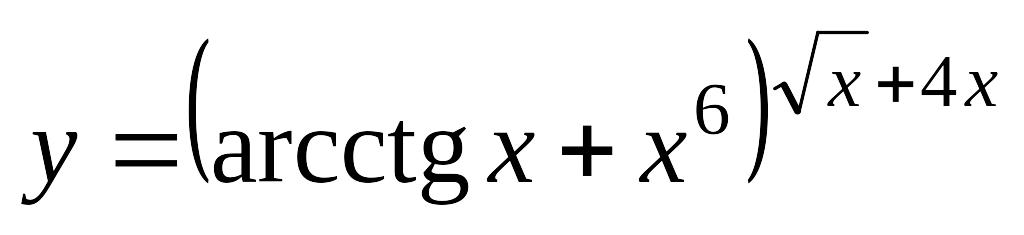 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
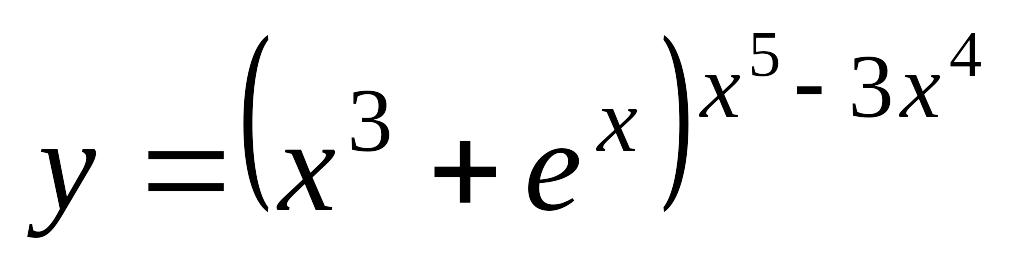 .
.а)
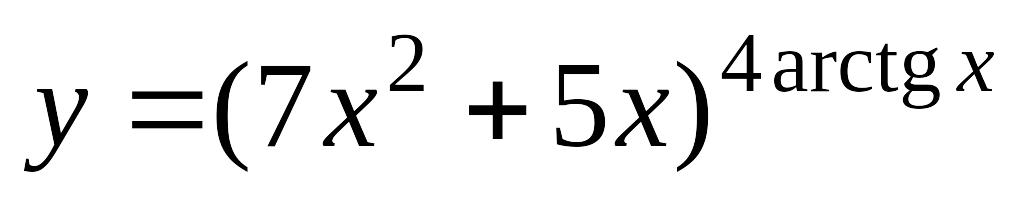 ; б)
; б)
 .
.а)
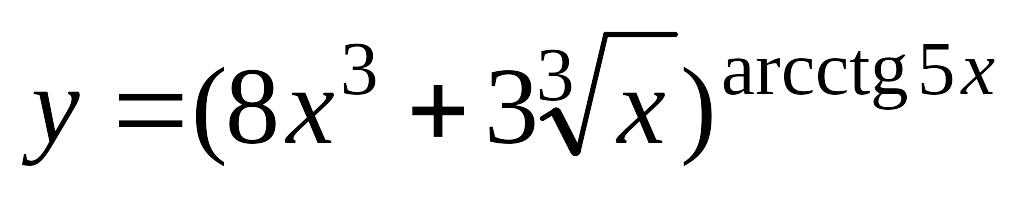 ; б)
; б)
 .
.а)
 ; б)
; б)
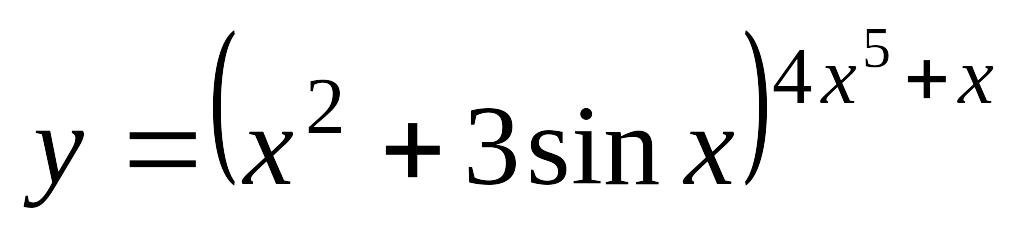 .
.а)
 ; б)
; б)
 .
.
Завдання 5. Знайти похідні другого порядку.
а)
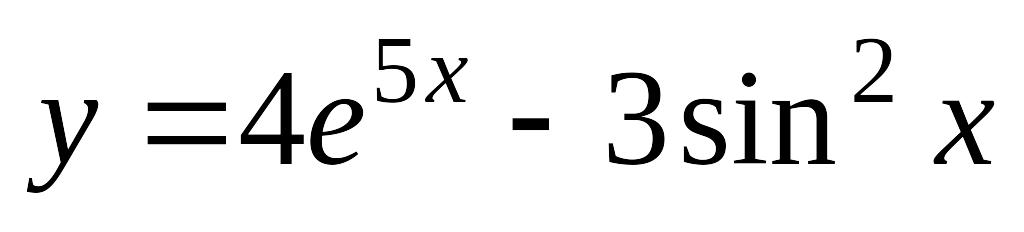 ; б)
; б) .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б) .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
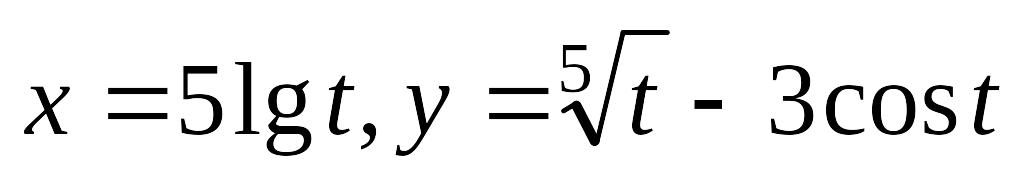 .
.а)
 ; б)
; б)
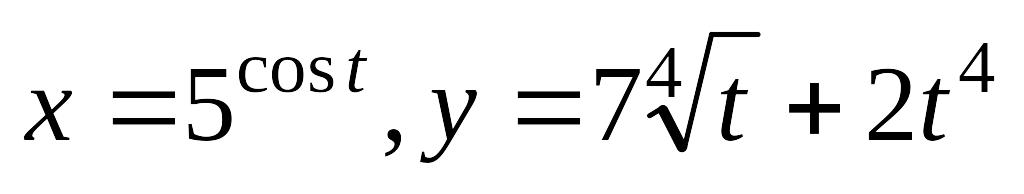 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 ;
;а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.
Завдання 6. Знайти диференціал функції і наближено обчислити її значення у заданій точці х.
1.
![]() .
2.
.
2.
![]() .
.
3.
![]() . 4.
. 4.
![]() .
.
5.
![]() . 6.
. 6.
![]() .
.
7.
![]() . 8.
. 8.
![]() .
.
9.
. 10.
![]() .
.
11.
![]() . 12.
. 12.
![]() .
.
13.
![]() . 14.
. 14.
![]() .
.
15.
![]() . 16.
. 16.
![]() .
.
17.
![]() . 18.
. 18.
![]() .
.
19.
![]() . 20.
. 20.
![]() .
.
21.
![]() . 22.
. 22.
![]() .
.
23.
![]() . 24.
. 24.
![]() .
.
25.
![]() . 26.
. 26.
![]()
27.
![]() . 28.
. 28.
![]() .
.
29.
![]() . 30.
. 30.
![]() .
.
Завдання
7.
Записати
рівняння дотичної і нормалі до кривої
![]() в точці з абсцисою
в точці з абсцисою
![]() .
.
1.
![]() . 2.
. 2.
![]() .
.
3.
![]() . 4.
. 4.
![]() .
.
5.
![]() . 6.
. 6.
![]() .
.
7.
![]() . 8.
. 8.
![]() .
.
9.
![]() . 10.
. 10.
![]() .
.
11.
![]() . 12.
. 12.
![]() .
.
13.
![]() . 14.
. 14.
![]() .
.
15.
![]() . 16.
. 16.
![]() .
.
17.
![]() . 18.
. 18.
![]() .
.
19.
![]() . 20.
. 20.
![]() .
.
21.
![]() . 22.
. 22.
![]() .
.
23.
![]() . 24.
. 24.
![]() .
.
25.
![]() . 26.
. 26.
![]() .
.
27.
![]() . 28.
. 28.
![]() .
.
29.
![]() . 30.
. 30.
![]() .
.
Завдання 8. Знайти границі, використовуючи правило Лопіталя.
а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
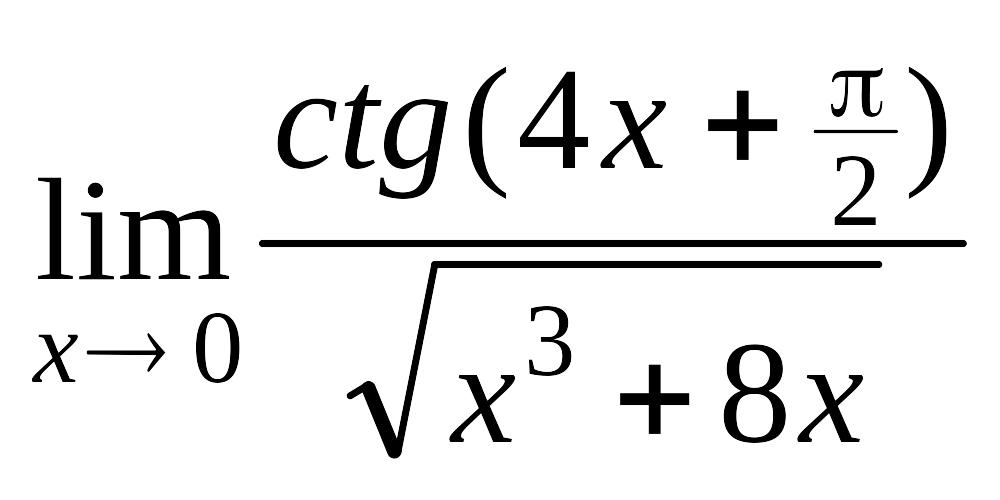 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
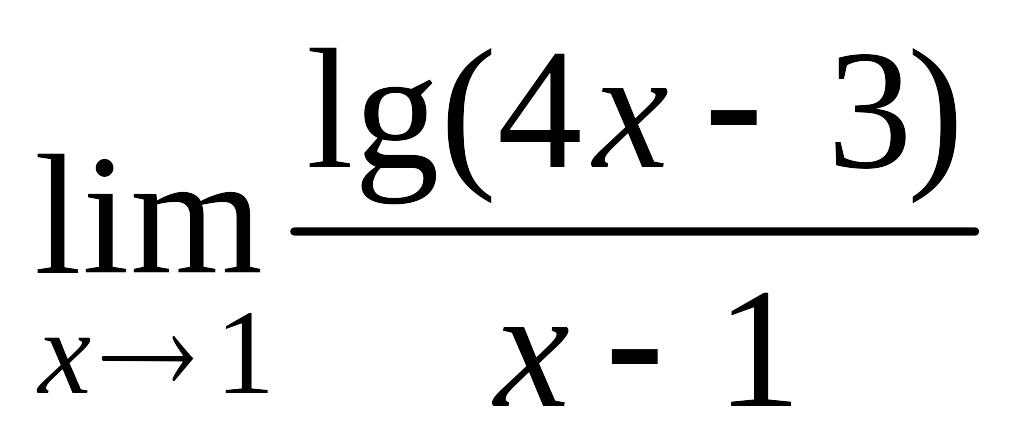 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
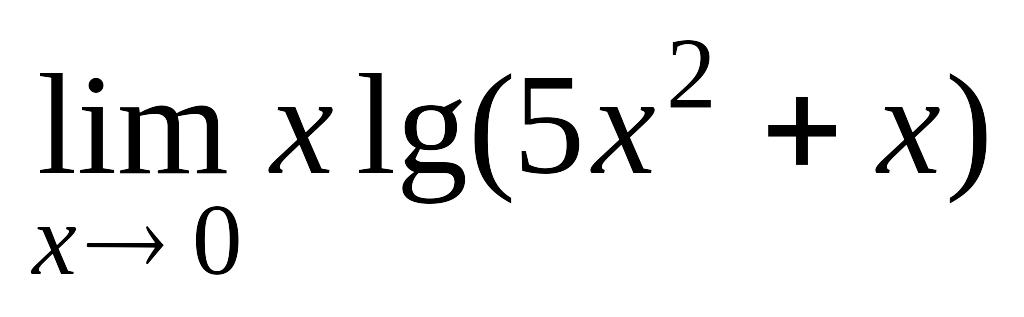 .
.а)
 ; б)
; б)

а)
 ; б)
; б)
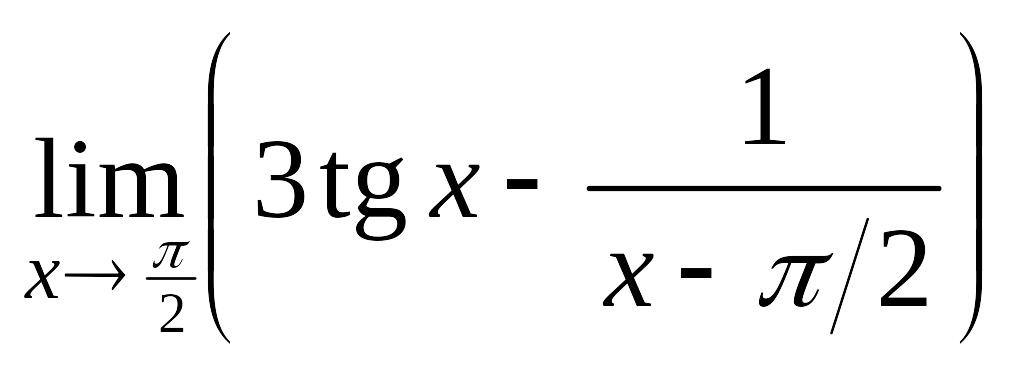 .
.а)
 ; б)
; б)
 .
.а)
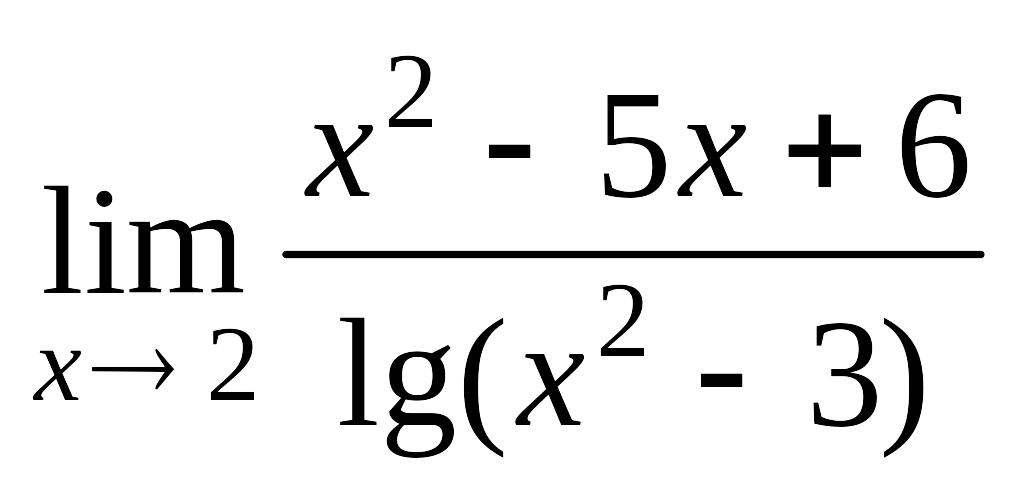 ; б)
; б)
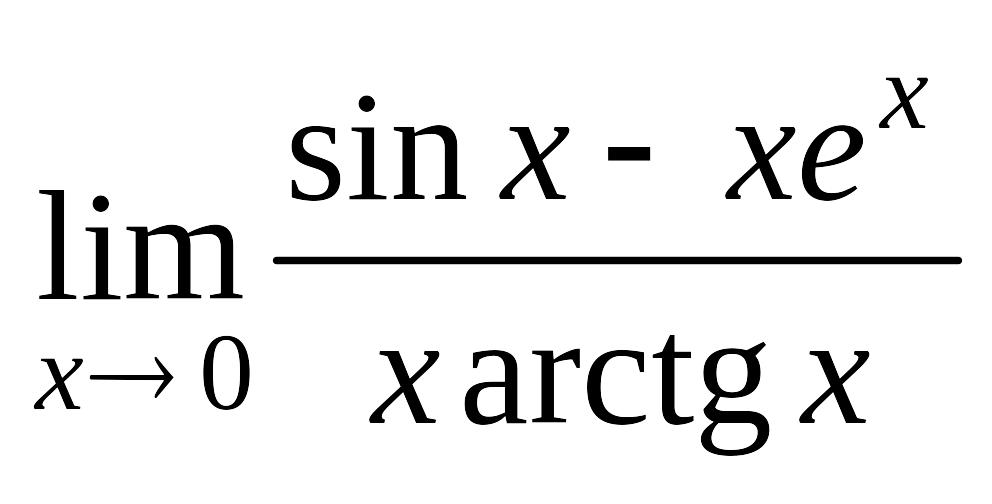 .
.а)
 ; б)
; б)
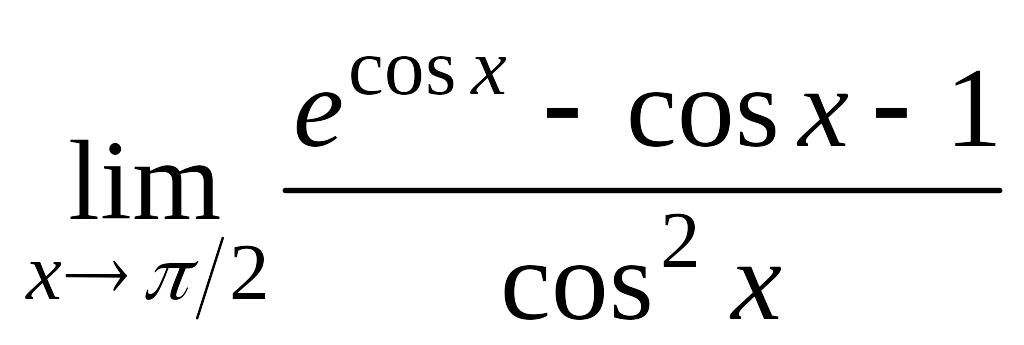 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
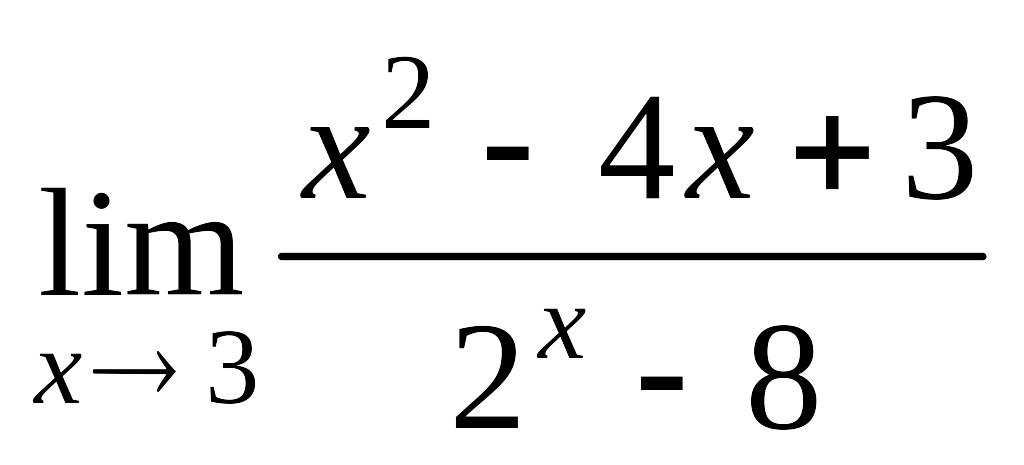 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.а)
 ; б)
; б)
 .
.
Завдання 9. Дослідити функцію і побудувати її графік.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
