§3.6. Інтегрування тригонометричних функцій.

Розглянемо інтеграл виду

. (6.1)

Тут і надалі R – раціональна функція своїх аргументів. Інтеграл (6.1) зводиться до інтеграла від раціональної функції за допомогою підстановки

. (6.2)

Вказана заміна змінної називається універсальною тригонометричною підстановкою. Враховуючи що

, , ,

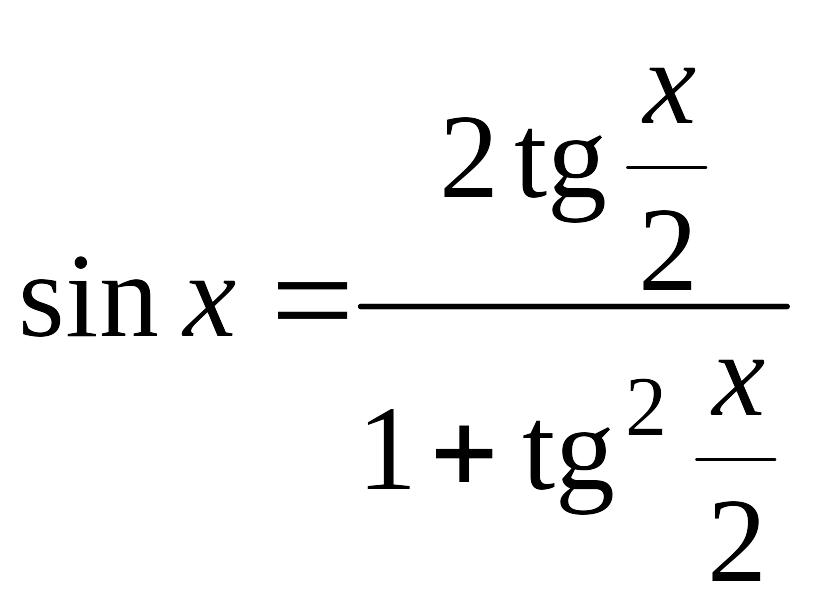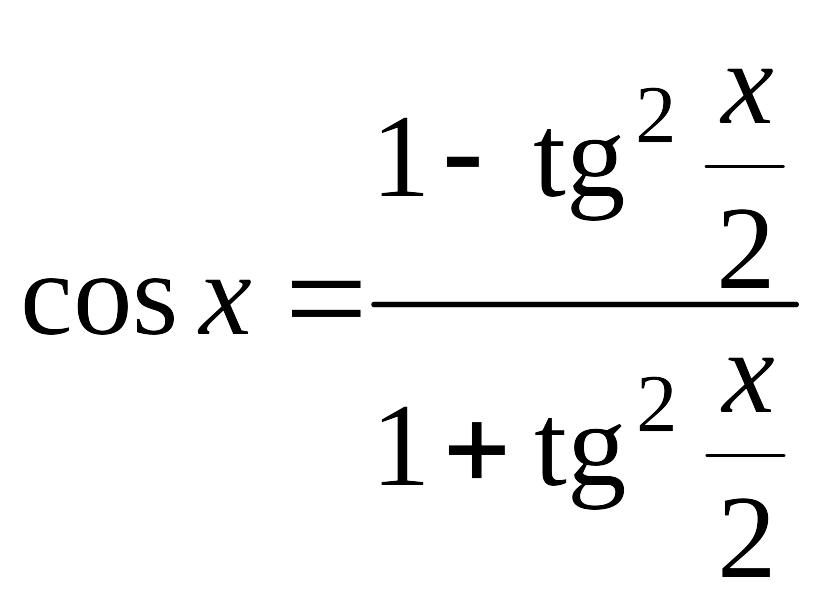дістаємо

. (6.3)

Приклад 1. Знайти інтеграл .

Розв’язання. Застосовуємо універсальну тригонометричну підстановку:

.

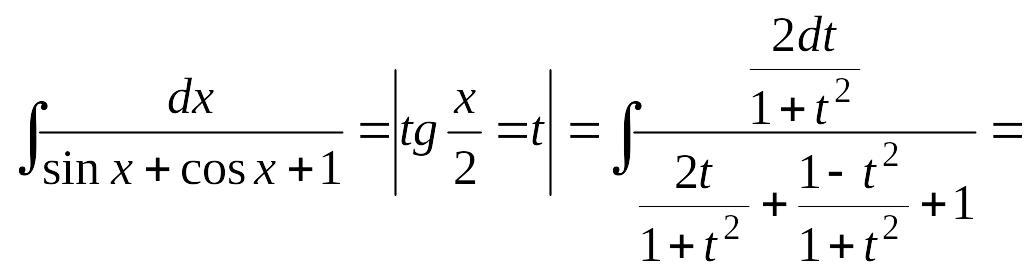
Недоліком підстановки (6.1) є те, що після її здійснення, як правило, під знаком інтеграла з’являються громіздкі вирази. Розглянемо деякі більш частинні випадки інтегралів від тригонометричних функцій.

1) Перший з інтегралів

, (6.4)

береться за допомогою підстановки , а другий – .

Приклад 2. Знайти інтеграл .

Розв’язання. Маємо перший з інтегралів (6.4). Можемо записати

.

2) Для інтегралів

, , (6.5)

де m i n – цілі числа, потрібно застосувати підстановку . для вказаної заміні отримуємо

,

;

.

Приклад 3. Знайти інтеграл .

Розв’язання. Маємо другий з інтегралів (6.5). Використовуючи заміну , дістаємо

.

3) Інтеграли

, , (6.6)

де p –додатне ціле число, беруться за допомогою підстановок , відповідно. Для цих інтегралів можемо записати

,

.

Приклад 4. Знайти інтеграл .

Розв’язання. Маємо другий з інтегралів (6.6). Робимо підстановку :

4) Для інтегралів

, (6.7)

де m i n – цілі невід’ємні числа, застосовуються тригонометричні формули, які дозволяють знизити степінь тригонометричних функцій у два рази, а саме

, , .

Приклад 5. Знайти інтеграл .

Розв’язання. Беремо інтеграл за допомогою формул зниження степеня:

5) Інтеграли

, , (6.8)

беруться за допомогою наступних тригонометричних формул (формул перетворення добутків у суми):

,

,

.

Приклад 6. Знайти інтеграл .

Розв’язання. Застосовуючи першу з наведених вище формул, дістаємо

.

§3.7. Інтегрування ірраціональних функцій

Інтеграл

(7.1)

зводиться до інтеграла від раціональної функції за допомогою підстановки

. (7.2)

Тут R – раціональна функція своїх аргументів, k – найменше спільне кратне (НСК) знаменників n, … , s.

Приклад 1. Обчислити інтеграл .

Розв’язання. У даному випадку підінтегральна функція раціонально залежить від аргументів i . Так як найменше спільне кратне чисел 4 і 2 дорівнює 4, то потрібно зробити підстановку :

.

Аналогічно попередньому, інтеграл

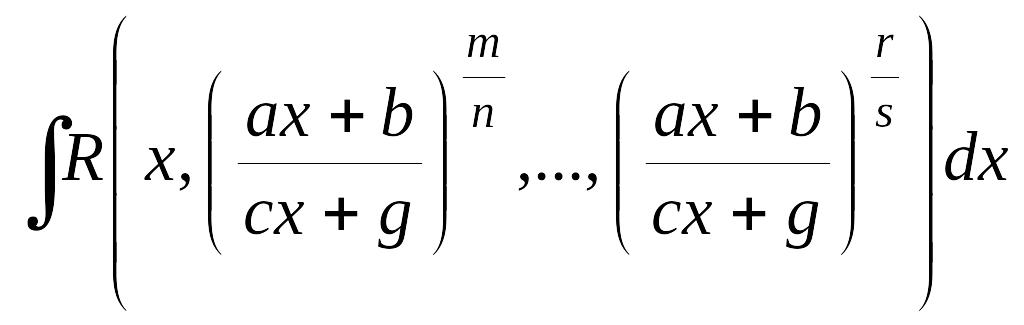(7.3)

зводиться до інтеграла від раціональної функції за допомогою підстановки

; ; , (7.4)

де k – НСК знаменників n, …, s.

Приклад 2. Знайти інтеграл .

Розв’язання. Маємо інтеграл типу (7.3). Робимо підстановку (7.4):

, , ,

;

.

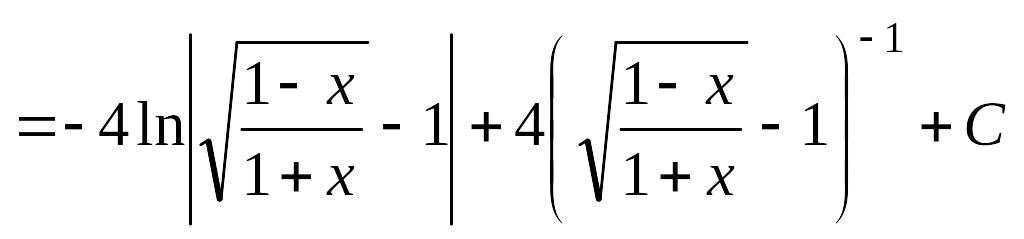Розглянемо інтеграл виду

(7.5)

Після виділення в квадратному тричлені повного квадрата і заміни змінної отримаємо один з трьох інтегралів, кожен з яких може бути знайдений при допомозі відповідної тригонометричної підстановки:

, ; (7.6)

, ; (7.7)

, . (7.8)

Приклад 3. Обчислити інтеграл .

Розв’язання. Виділяємо в знаменнику повний квадрат і робимо першу підстановку:

.

Отримали інтеграл (7.6). Робимо вказану підстановку і, враховуючи, що , дістаємо

.

Останній інтеграл береться за допомогою універсальної тригонометричної підстановки:

.

Розділ 4. Визначений інтеграл. Застосування визначеного інтеграла.