1.3 Физико-математическая модель второго уровня для расчета рабочего цикла двс

Физико-математическая модель второго уровня имеет две модификации. Первая из них составлена с учетом изменения состава рабочего тела в цилиндре. Во второй модификации влияние изменения состава учтено приближенно; в процессах впуска и сжатия рабочим телом считается воздух, в процессах расширения и выпуска  продукты сгорания. Применение модели второй модификации существенно упрощает вычислительные процедуры и мало влияет на точность расчета. Поэтому далее описана ФММ второго уровня второй модификации.

Кроме того в данной модели расчет выполняют для основных процессов (сжатия, сгорания, расширения) при изменении угла поворота кривошипа в пределах  = 180 ... 540 для четырехтактного двигателя. Влияние процессов при впуске и выпуске учтено суммарно по статистическим данным.

Рассматриваемая ФММ включает в себя четыре основных дифференциальных уравнения:

 первое кинематическое уравнение, или уравнение изменения объема рабочей полости;

 уравнение баланса массы;

 уравнение энергетического баланса;

 уравнение состояния рабочего тела

и ряд других дополнительных уравнений в дифференциальной или конечной форме. Эти дополнительные уравнения необходимы для определения величин, входящих в виде отдельных членов или множителей в основные уравнения.

Первое кинематическое уравнение вытекает из формулы для определения текущего объема рабочей полости в соответствии с закономерностями кривошипно-шатунного механизма:

, (1)

где V_c  объем камеры сжатия,

F_n  площадь поршня,

r_к  радиус кривошипа,

 отношение радиуса кривошипа к длине шатуна,

  угол поворота кривошипа .

После дифференцирования формулы (1) получаем первое кинематическое уравнение в дифференциальной форме:

. (2)

В ФММ второго уровня второй модификации процессы газообмена не рассматриваются. Состояние рабочего тела и его масса в начале сжатия (точка “а”) оценивается приближенно (см. раздел “Исходные данные для расчета”). Поэтому масса рабочего тела в процессах сжатия - расширения изменяется только за счет добавки топлива при его испарении и сгорании. В целом эта добавка сравнительно невелика, а характер протекания процессов испарения и сгорания достаточно сложен. Поэтому приближенно будем относить изменение массы рабочего тела к процессу сгорания.

В дизельных ДВС добавка топлива по массе составляет 3 - 4% от общего количества рабочего тела, а процесс сгорания отстает от процесса испарения обычно на несколько градусов поворота коленчатого вала (пкв). Поэтому общая погрешность принятого выше допущения невелика.

В бензиновых ДВС относительная добавка топлива по массе больше (6 - 7% от общего количества рабочего тела), испарение бензина начинается в карбюраторе, продолжается во впускном коллекторе и завершается в цилиндре. Однако учесть закономерности такого процесса испарения затруднительно, поэтому принятое ранее допущение распространено и на бензиновые ДВС.

В газовых двигателях подобная проблема не возникает в связи с отсутствием процесса испарения.

В соответствии с принятой выше гипотезой изменение массы рабочего тела равно:

, (3)

где m_{т ц}  цикловая массовая подача топлива,

х  массовая доля топлива, сгоревшего в цилиндре к рассматриваемому моменту времени.

В процессах сжатия и расширения dx = 0 и dm = 0, то есть масса рабочего тела неизменна.

Соотношение (3) является уравнением материального (массового) баланса в цилиндре ДВС.

Уравнение энергетического баланса в цилиндре составлено на основе первого закона термодинамики для закрытой нетеплоизолированной системы и имеет вид:

, (4)

где Т  абсолютная температура рабочего тела,

с_v  удельная теплоемкость рабочего тела при постоянном объеме,

dQ_c  элементарное количество теплоты, подведенное к рабочему телу за счет сгорания,

dQ_w  элементарное количество теплоты за счет внешнего теплообмена (теплообмена со стенками),

k  показатель адиабаты рабочего тела.

Уравнение (4) составлено с учетом изменения массы рабочего тела, а также теплового (dQ_c и dQ_w) и механического взаимодействия с внешней средой.

Система основных уравнений замыкается с помощью уравнения состояния рабочего тела, которое в конечной форме имеет вид:

рV = RmT , (5)

где R  газовая постоянная для рабочего тела,

или в дифференциальной форме

. (6)

Система уравнений (2), (3), (4) и (6) в дифференциальной форме и является математической формулировкой ФММ второго уровня:

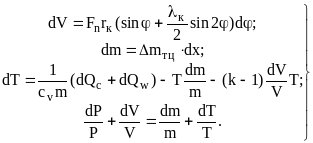(7)

Система (7) состоит из обыкновенных нелинейных дифференциальных уравнений с переменными коэффициентами. Современными аналитическими методами такая система не может быть решена. Поэтому она решается численными методами с применением компьютерной техники. Конечной целью решения системы являются функции V(); m(); T(); Р().

Для отыскания частного решения системы (7) она сопровождается дополнительными уравнениями, позволяющими на каждом расчетном шаге определять необходимые слагаемые и множители. К числу дополнительных уравнений относятся следующие.

Элементарное количество теплоты, подведенное к рабочему телу при сгорании:

, (8)

где Hu  действительная теплота сгорания топлива.

Величина Hu зависит от рода топлива и состава смеси (коэффициент избытка воздуха ):

где Huт  теоретическая теплота сгорания (при полном сгорании

топлива), Дж/кг,

L₀  теоретически необходимое количество воздуха для сгорания 1 кг топлива, кмоль/кг.

При составлении формул (9) принято, что в стехиометрической смеси ( = 1) и бедной смеси ( > 1) топливо сгорает полностью, а в богатой смеси ( < 1) имеет место химическое недогорание вследствие недостатка кислорода, за счет чего действительная теплота сгорания уменьшается.

Закономерность тепловыделения при сгорании описывается полуэмпирической формулой И.И. Вибе, полученной на основе кинетической теории сгорания и с учетом опытных данных, полученных при испытаниях многих двигателей разных типов:

,(10)

где m₁  показатель сгорания, зависящий от типа двигателя (способа смесеобразования);

_с и _z  углы поворота кривошипа, соответствующие началу процесса сгорания и его концу.

Коэффициент 6,908 в уравнении (10) получен при условии, что к концу сгорания доля сгоревшего топлива составляет 0,999. Расчет функции х ведут в диапазоне _с    _z, в других случаях, когда   _z или   _z , принимают dx = 0, что означает отсутствие сгорания.

Элементарное количество теплоты за счет теплообмена со стенками определяют по формуле Ньютона-Рихмана:

, (11)

где _w  коэффициент теплоотдачи на границе рабочее тело - твердая стенка,

F_w  площадь поверхности теплоотдачи,

T_w  температура стенки,

  угловая скорость вращения кривошипа.

В течение рабочего цикла ДВС возможны разные соотношения между температурами T_w и Т(T_w ^_ Т).Если T_w>Т, то величина dQ_w >0, что означает наличие подвода теплоты от стенок к рабочему телу (такое положение имеет место при впуске и в начале сжатия). Если T_w < Т, то величина dQ_w < 0, при этом теплота отводится от рабочего тела в стенку (при сгорании, расширении, выпуске). Если T_w = Т, то величина dQ_w = 0; теплообмен с внешней средой отсутствует, такое положение возможно только в определенной момент в процессе сжатия; соответствующая точка на индикаторной диаграмме называется квазиадиабатной.

В формуле (11) величина Т_w представляет собой осредненную температуру всех поверхностей, образующих рабочую полость (поршня, крышки, клапанов, цилиндра). В течение цикла величина Т_w считается постоянной вследствие большой тепловой инерции стенок, окружающих рабочую полость. В случаях, когда наблюдается значительное различие температур, указанных деталей или на одной из деталей имеется существенная температурная неравномерность, приходится учитывать локальный характер теплообмена:

, (11,a)

где j  количество учтенных поверхностей с разными температурами.

Площади поверхностей поршня, крышки и клапанов зависят от размеров и конфигурации этих поверхностей, для данного двигателя они постоянны.

Площадь поверхности цилиндра изменяется в связи с перемещением поршня, она зависит от угла поворота кривошипа и выражается вторым кинематическим уравнением:

, (12)

где D  диаметр цилиндра,

S_o  минимальное расстояние между поршнем и крышкой при положении поршня в ВМТ, величина S_o зависит главным образом от степени сжатия.

Коэффициент теплоотдачи _ зависит от условий теплообмена на границе “газ - стенка”, то есть от многих факторов, которые влияют на формирование пограничного слоя (плотности, вязкости газа, локальной скорости, наличия отложений на стенке и т.д.). В ДВС положение значительно осложняется нестационарными явлениями в течение цикла, периодическим характером процессов. Поэтому для определения коэффициента теплоотдачи _ применяют эмпирические формулы разных авторов (Эйхельберга, Пфлаума, Вошни, Розенблита).

В данной модели применяется формула Пфлаума:

, (13)

где Р_к  давление наддува,

Р_о  атмосферное давление.

Таким образом, дополнительными уравнениями являются формулы (8) - (13).

Для получения частного решения задачи с помощью системы (7) необходимы начальные и граничные условия. Поскольку процесс в ДВС периодический, то в принципе начальные условия могут быть любые, так как в процессе счета они последовательно уточняются. Выбрав произвольные начальные условия, выполняют весь цикл расчетов, и в конце цикла мы должны вернуться в исходную точку. Очевидно, при произвольных начальных условиях мы получим конечный результат, отличающийся от начальных данных. Тогда рассчитывают второй цикл, в котором начальные условия соответствуют конечным из первого цикла. Расчеты продолжают до тех пор, пока конечные результаты будут тождественны начальным (с учетом допустимой погрешности). Такой метод нахождения действительных начальных условий называется методом установления. Произвольный выбор начальных условий при этом не влияет на результат, а влияет на количество расчетных циклов для достижения установления.

К граничным условиям в данной задаче относятся: основные размеры двигателя (D, F_n, r_к, _к, F_wj, S_o), условия на входе (Р_к; T_к или Р_o, T_o), температура стенок Т_wj, характеристики процесса сгорания (Huт, , L_o, m₁, _z, _c). Все эти величины выбирают или оценивают в зависимости от конкретного типа двигателя, режима работы, условий эксплуатации, к их выбору нужно отнестись внимательно, так как от них зависит конечный результат.

Систему уравнений (7) решают числено на ЭВМ одним из известных методов. Среди них наиболее распространены методы Эйлера, Рунге-Кутта, Адамса, Штермера. В данном курсовом проекте применен модифицированный метод Эйлера, составленная программа имеет шифр DVS-2.

Таким образом, численное решение основной системы уравнений (7) с учетом дополнительных соотношений (8) - (13) позволяет получить функции V(), m(), T(), p(). Это дает возможность построить индикаторные диаграммы развернутые T() и Р() или свернутые T(V) и Р(V). Они используются для дальнейшего анализа.

Другой важной целью теплового расчета является определение цикловых энергетических показателей, а именно:

индикаторной работы цикла

, (14)

индикаторной мощности одного цилиндра

, (15)

где n  частота вращения вала,

  коэффициент тактности, который равен  = 2 для четырехтактных и  = 1 для двухтактных ДВС (множитель в формуле (15) показывает количество циклов в единицу времени);

индикаторной мощности двигателя

, (16)

где і  число цилиндров;

среднего индикаторного давления

, (17)

где  рабочий объем цилиндра,

S  ход поршня.

К числу экономических показателей относятся:

индикаторный кпд

, (18)

удельный индикаторный расход топлива

, (19)

где числовой коэффициент получен при условии, что величину g_i измеряют в кг/кВтчас.

Тепловой расчет на этом завершается, данные теплового расчета используются в динамическом расчете.