4 Динамика
130. Динамика - раздел теоретической механики, в котором изучается движение материальных тел с учетом действующих на них сил (в связи с механическим взаимодействием их с другими телами).
Основные аксиомы динамики
Основу динамики составляют законы классической механики Галилея - Ньютона (так называемые аксиомы динамики): закон инерции, закон пропорциональности силы и ускорения, закон равенства действия и противодействия, закон независимости действия сил.
131. Закон инерции - материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока действие других тел не изменит это состояние.
132. Инерция (инерционность) - свойство материальных тел, заключающееся в стремлении их сохранять неизменной скорость своего движения (или состояние покоя), т.е. сохранять данное кинематическое состояние.
133. Мерой инерции материальных тел являются: масса (при поступательном движении); момент инерции (при вращении). Масса - количество материи данного вида в данной точке (в данном объеме).
134. Момент
инерции точки - величина, равная
произведению массы
![]() точки на квадрат ее кратчайшего
расстояния
точки на квадрат ее кратчайшего
расстояния
![]() до оси (центра) вращения,
до оси (центра) вращения,
![]() ,
кг
м2.
,
кг
м2.
Масса определяет инерционность тела только при поступательном движении, так как в этом случае скорости и ускорения всех точек тела в данный момент времени геометрически равны. При вращении вокруг оси инерционность тела определяется не только массой тела, но и тем как масса распределена окрест оси вращения. Чем компактнее (ближе к оси) распределена масса тела, тем меньше инерционность тела и наоборот. Поэтому при вращении тела вокруг оси его инерционность определяет момент инерции тела. Различают моменты инерции тела относительно: точки (начала декартовой системы координат); оси (координатных осей); плоскости (координатных плоскостей).
135. Момент инерции тела относительно точки (оси, плоскости) - величина, равная предельному значению суммы произведений масс элементарных частиц тела на квадрат их кратчайшего расстояния до точки, (оси, плоскости),
![]() ,
кг
.м2.
,
кг
.м2.
136. Закон пропорциональности силы и ускорения - ускорение материальной точки пропорционально приложенной к ней силе и имеет одинаковое с ней направление, - основное уравнение динамики (рисунок 17).
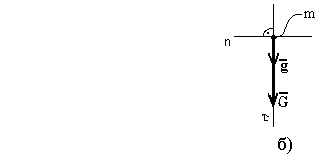
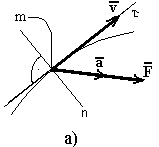
Рисунок 18 - Движение точки по кривой - а; падение в поле тяжести - б
137. Законы инерции и пропорциональности силы и ускорения справедливы для инерциальных систем отсчета. Инерциальные системы отсчета - системы отсчета неподвижные, связанные с землей или движущиеся прямолинейно и равномерно.
138. Закон
равенства действия и противодействия
- при взаимодействии двух тел, силы
приложенные к каждому из них, равны по
модулю и направлены по одной прямой в
противоположные стороны. Например
![]() ,
где
,
где
![]() -
сила действия на рассматриваемую точку
со стороны тела,
-
сила действия на рассматриваемую точку
со стороны тела,
![]() - сила противодействия телу со стороны
точки (сила инерции
- сила противодействия телу со стороны
точки (сила инерции
![]() ),
),
![]() (рисунок
19а), см. также рисунок 18а.
(рисунок
19а), см. также рисунок 18а.
139. Сила
инерции материальной точки - сила
противодействия телу сообщающему точке
ускорение
![]() ,
равная:
,
равная:
![]()
![]() ,
где
,
где
![]() - касательная составляющая силы инерции,
пропорциональная касательной составляющей
- касательная составляющая силы инерции,
пропорциональная касательной составляющей
![]() полного ускорения
полного ускорения
![]() точки;
точки;
![]() -
нормальная составляющая силы инерции,
пропорциональная нормальной
-
нормальная составляющая силы инерции,
пропорциональная нормальной
![]() составляющей полного ускорения
составляющей полного ускорения![]() ,
см. рисунок 19а.
,
см. рисунок 19а.
Р
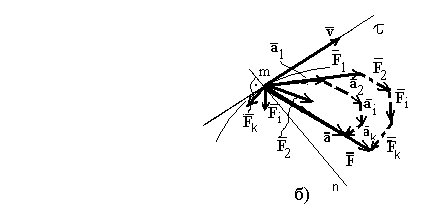 исунок
19 - Сила действия и сила инерции - а;
сложение ускорений - б
исунок
19 - Сила действия и сила инерции - а;
сложение ускорений - б
140. Закон
независимости действия сил - несколько
одновременно действующих на материальную
точку сил
![]() сообщают точке такое ускорение
,
какое сообщила бы ей одна сила
сообщают точке такое ускорение
,
какое сообщила бы ей одна сила
![]() ,
равная их геометрической сумме
,
равная их геометрической сумме
![]() ,
т.е.
,
т.е.
![]() ,
где
,
где
![]() - ускорение точки, сообщаемое точке
i-ой силой (рисунок 18б).
- ускорение точки, сообщаемое точке
i-ой силой (рисунок 18б).
Динамика материальной точки
Записав
основное уравнение динамики
![]() ,
где
,
где
![]() в проекциях на оси декартовой и
естественной систем координат, см.
рисунок 18 и рисунок 12, получим
дифференциальные уравнения движения
свободной материальной точки в декартовых
и естественных координатах:
в проекциях на оси декартовой и
естественной систем координат, см.
рисунок 18 и рисунок 12, получим
дифференциальные уравнения движения
свободной материальной точки в декартовых
и естественных координатах:
135.
 136.
136.

В случае
движения несвободной материальной
точки по неподвижной шероховатой кривой
дифференциальные уравнения в правой
части будут содержать проекции на
оси систем координат касательной
(сила
![]() трения)
и нормальной
составляющих
полной реакции этой кривой (твердой
шероховатой поверхности), как связи,
см. рис. 20б.
трения)
и нормальной
составляющих
полной реакции этой кривой (твердой
шероховатой поверхности), как связи,
см. рис. 20б.
В динамике материальной точки решаются (в частности) две так называемые основные задачи: 1-я (прямая);
2-я (обратная).
141. 1-я (прямая) задача динамики точки - задача об определении сил по заданному движению точки.
142. 2-я (обратная) задача динамики точки - задача об определении движения точки по заданным силам.
При решении этих задач исходными являются дифференциальные уравнения движения точки, записанные в общем виде в декартовых или естественных координатах.
Некоторые задачи динамики материальной точки решаются с применением принципа Германа-Эйлера-Даламбера (принцип Даламбера), иначе говоря методом кинетостатики, который формулируется и записывается следующим образом.
Для свободной материальной точки (рисунок 20а).
143. Движущаяся
свободная материальная точка может
рассматриваться как покоящаяся в
том или ином рассматриваемом положении
под действием активных (задаваемых)
сил и силы инерции,
т.е.
![]() -
условие псевдопокоя свободной точки
под действием сил, сходящихся в точке.
-
условие псевдопокоя свободной точки
под действием сил, сходящихся в точке.
Р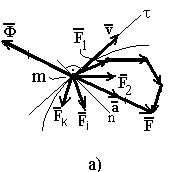 исунок
20 - К применению принципа Д`Aламбера
для свободной - а; несвободной - б точки
исунок
20 - К применению принципа Д`Aламбера
для свободной - а; несвободной - б точки
Для несвободной материальной точки (рисунок 20б).
1 44.
Движущаяся несвободная материальная
точка может рассматриваться как
покоящаяся в том или ином рассматриваемом
положении под действием активных сил,
реакций связи и силы
инерции, т.е.
44.
Движущаяся несвободная материальная
точка может рассматриваться как
покоящаяся в том или ином рассматриваемом
положении под действием активных сил,
реакций связи и силы
инерции, т.е.
![]() -
условие псевдопокоя несвободной точки
под действием сил, сходящихся в точке,
где
-
условие псевдопокоя несвободной точки
под действием сил, сходящихся в точке,
где
![]() ,
т.о.
,
т.о.
![]()
При решении задач уравнения (143) и (144) записываются в аналитической форме, т.е. в проекциях на оси декартовой (или естественной) систем координат.
Различают две меры действия силы и две меры механического движения (рисунок 21). При этом одна из мер - величина векторная, другая - скалярная.
Р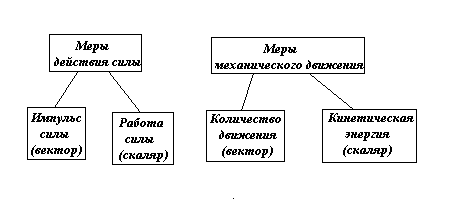 исунок
21 - Меры действия силы и механического
движения
исунок
21 - Меры действия силы и механического
движения
145. Импульс
силы - вектор
![]() ,
динамический параметр, величина,
характеризующая передачу материальной
точке механического движения со
стороны действующего на нее тела за
данный промежуток
,
динамический параметр, величина,
характеризующая передачу материальной
точке механического движения со
стороны действующего на нее тела за
данный промежуток
![]() времени, и учитывающий (в отличие
от силы) и интенсивность, и продолжительность
механического взаимодействия.
времени, и учитывающий (в отличие
от силы) и интенсивность, и продолжительность
механического взаимодействия.
146. Импульс
постоянной по величине и направлению
силы (![]() ) равен произведению вектора силы на
интервал времени ее действия,
) равен произведению вектора силы на
интервал времени ее действия,
![]() ,
Н·м.
,
Н·м.
147. Импульс переменной
по величине и (или) направлению силы
(![]() )
равен:
)
равен:
 ,
,
где
![]() и
и
![]() - момент начала и конца действия
переменной силы
- момент начала и конца действия
переменной силы
![]() ,
время действия силы
,
время действия силы
![]() .
.
148. Работа силы - алгебраическая величина, характеризующая передачу точке (телу) механического движения со стороны действующего на не тела (точки) при перемещении точки (тела) на некотором пути.
149. Работа
силы, постоянной по величине и
направлению, (
)
на конечном перемещении
![]() материальной точки равна скалярному
произведению вектора силы на вектор
перемещения:
материальной точки равна скалярному
произведению вектора силы на вектор
перемещения:
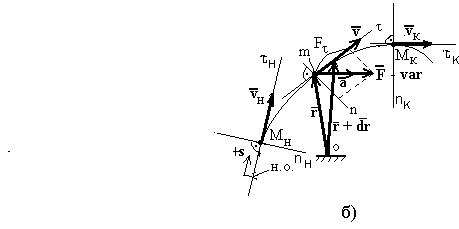

![]() (рисунок 22а).
(рисунок 22а).
Рисунок 22 - К определению работы силы постоянной - а; переменной - б
150. Работа
силы, переменной по величине и
(или) направлению, (![]() )
на конечном перемещении материальной
точки равна значению криволинейного
интеграла взятого от выражения для
элементарной работы этой силы на
элементарном перемещении точки:
)
на конечном перемещении материальной
точки равна значению криволинейного
интеграла взятого от выражения для
элементарной работы этой силы на
элементарном перемещении точки:
 (рисунок
22б), где
(рисунок
22б), где
![]() - элементарный путь, пройденный точкой
за элементарный интервал
- элементарный путь, пройденный точкой
за элементарный интервал
![]() времени;
времени;
![]() - элементарное приращение дуговой
координаты точки;
- элементарное приращение дуговой
координаты точки;
![]() -
-
![]() - орт касательной;
- орт касательной;
![]() -
элементарное приращение радиус-вектора
точки;
-
элементарное приращение радиус-вектора
точки;
![]() - проекции силы
на оси декартовой системы координат:
- проекции силы
на оси декартовой системы координат:
![]() - элементарное приращение координат
- элементарное приращение координат
![]() точки;
точки;
![]() - проекция силы на касательную к траектории
в данной точке;
- проекция силы на касательную к траектории
в данной точке;
![]() .
.
151. Мощность
![]() постоянной силы - отношение
элементарного приращения работы
постоянной силы - отношение
элементарного приращения работы
![]() силы
силы
![]() к
элементарному интервалу времени
,
в течении которого имело место это
приращение, т.е. - работа совершаемая в
единицу времени:
к
элементарному интервалу времени
,
в течении которого имело место это
приращение, т.е. - работа совершаемая в
единицу времени:
![]()
152. Работа равнодействующей силы
![]() на некотором перемещении равна
алгебраической сумме работ ее составляющих
на некотором перемещении равна
алгебраической сумме работ ее составляющих
![]() на
том же перемещении:
на
том же перемещении:
![]() .
.
153. Работа постоянной силы
на результирующем перемещении
![]() равна алгебраической сумме работ
этой силы на составляющих
равна алгебраической сумме работ
этой силы на составляющих![]() перемещениях:
перемещениях:
![]() .
.
154.
Количество движения
![]() материальной точки - вектор, имеющий
направление вектора скорости
и модуль, равный произведению массы
точки на модуль скорости ее движения:
материальной точки - вектор, имеющий
направление вектора скорости
и модуль, равный произведению массы
точки на модуль скорости ее движения:
![]() (рисунок 23а).
(рисунок 23а).
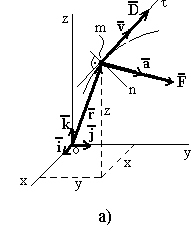
Р исунок
23- Количество движения точки - а; и момент
количества движения - б
исунок
23- Количество движения точки - а; и момент
количества движения - б
155. Производная от вектора количества движения точки по времени равна равнодействующей всех сил, действующих на точку:
![]() .
.
156. Приращение вектора количества движения точки за конечный интервал времени равно геометрической сумме импульсов всех сил, действующих на точку в течении этого интервала времени:
![]() или
или
![]()
157. Записав уравнение (156) в проекциях на оси декартовой системы координат, получим:
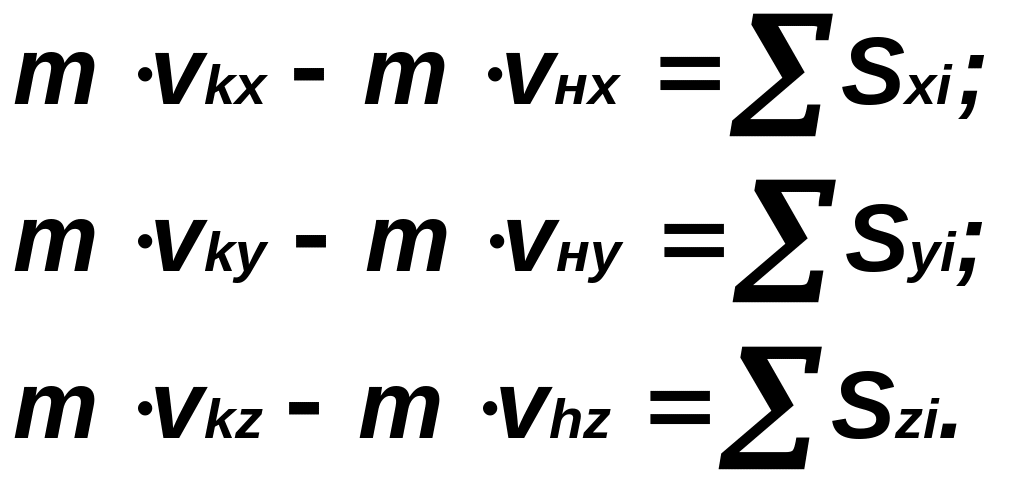
Уравнения (155-157) - разные формы записи теоремы об изменении количества движения материальной точки: дифференциальная векторная, векторная конечная и аналитическая конечная соответственно.
В случае,
когда
![]() или, например
или, например
![]() ,
уравнения (156) и (157) называют законом
сохранения количества движения
материальной точки в целом (
,
уравнения (156) и (157) называют законом
сохранения количества движения
материальной точки в целом (![]() )
или - в проекции на ось
)
или - в проекции на ось
![]() в частности (
в частности (![]() ).
).
158. Момент
количества движения материальной
точки относительно центра О - вектор
![]() ,
направленный перпендикулярно плоскости,
проходящей через вектор
количества
движения точки и центр
в
ту сторону, смотря откуда вектор
виден
направленным против вращения часовой
стрелки, и равный:
,
направленный перпендикулярно плоскости,
проходящей через вектор
количества
движения точки и центр
в
ту сторону, смотря откуда вектор
виден
направленным против вращения часовой
стрелки, и равный:
![]() (рисунок 23б).
(рисунок 23б).
159. Момент
количества движения материальной
точки относительно оси - алгебраическая
величина, взятая со знаком плюс или
минус, и равная произведению модуля
проекции
![]() вектора количества движения
точки на плоскость
,
перпендикулярную оси
вектора количества движения
точки на плоскость
,
перпендикулярную оси
![]() ,
на плечо
,
на плечо
![]() этой проекции относительно этой оси
:
этой проекции относительно этой оси
:
![]() (рисунок 23б).
(рисунок 23б).
160. Производная от вектора момента количества движения точки относительно центра по времени равна главному моменту всех сил, действующих на точку, относительно этого центра:
![]() .
.
161. Записав уравнение (160) в проекциях на оси декартовой системы координат, получим:
![]()
Уравнения (160) и (161) - теорема об изменении момента количества движения точки, записанная в дифференциальной векторной и аналитической формах соответственно,
В случае,
когда
![]() или, например
или, например
![]() ,
уравнения (160) и (161) называются законом
сохранения момента количества движения
точки относительно центра (
,
уравнения (160) и (161) называются законом
сохранения момента количества движения
точки относительно центра (![]() )
или - оси (
)
или - оси (![]() ).
).
162. Приращение
![]() кинетической энергии
кинетической энергии
![]() материальной точки при ее движении
на некотором пути равно сумме работ
всех сил, действующих на точку на
этом пути:
материальной точки при ее движении
на некотором пути равно сумме работ
всех сил, действующих на точку на
этом пути:![]() , где
, где
![]() ,
,
![]() ,
,
![]() -
кинетическая энергия точки в конечном
и начальном положениях.
-
кинетическая энергия точки в конечном
и начальном положениях.
163. Кинетическая
энергия точки - скалярная мера
механического движения, равная половине
произведения массы точки на квадрат
скорости ее движения:
![]() ,
(
- всегда положительный скаляр).
,
(
- всегда положительный скаляр).
Динамика твердого тела и механической системы
Все силы, действующие на механическую систему, делятся на внешние и внутренние. Ко внешним силам относятся активные (задаваемые) силы и реакции внешних связей. Ко внутренним силам относят реакции внутренних связей - силы взаимодействия между телами (точками), входящими в рассматриваемую систему тел (точек).
164. Свойство
системы внутренних сил - главный
момент
![]() и главный вектор
и главный вектор
![]() внутренних сил равны нулю (
внутренних сил равны нулю (![]() ,
,
![]() ),
так как все внутренние силы, являясь
силами действия и противодействия между
отдельными телами (точками) системы,
попарно равны по модулю и противоположны
по направлению.
),
так как все внутренние силы, являясь
силами действия и противодействия между
отдельными телами (точками) системы,
попарно равны по модулю и противоположны
по направлению.
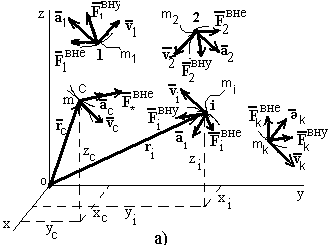 165.
Центр масс системы материальных
точек - точка, радиус-вектор
165.
Центр масс системы материальных
точек - точка, радиус-вектор
![]() которой определяется уравнением:
которой определяется уравнением:
![]() , где
, где
![]() и
и
![]() масса и радиус-вектор i-ой
точки механической системы (рисунок
24а).
масса и радиус-вектор i-ой
точки механической системы (рисунок
24а).
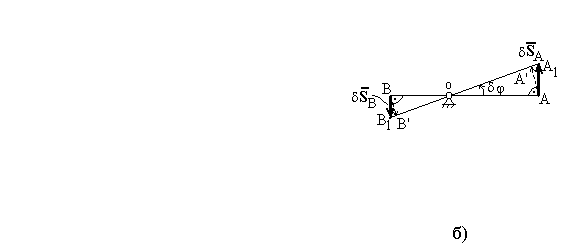
Рисунок 24 - К определению центра масс - а;
возможные
перемещения: угловое
![]() рычага
рычага![]() и линейные
и линейные
![]() его точек
и
его точек
и
![]() - б
- б
166. Записав уравнение (165) в проекциях на оси декартовой системы координат, получим выражения для координат центра масс
![]() ,
,
![]() ,
,
![]() ,
см. рисунок 24а.
,
см. рисунок 24а.
167. Центр масс
системы материальных точек движется
как материальная точка
![]() массой
равной массе всей системы
массой
равной массе всей системы
![]() ,
к которой приложены все внешние силы
,
к которой приложены все внешние силы![]() ,
действующие на систему, -
теорема о движения центра
масс:
,
действующие на систему, -
теорема о движения центра
масс:
![]() -
II-ой закон Ньютона (основное
уравнение динамики) для центра масс.
-
II-ой закон Ньютона (основное
уравнение динамики) для центра масс.
Здесь
![]() -
равнодействующая, соответственно,
внешних и внутренних сил, действующих
на i -ую материальную точку.
-
равнодействующая, соответственно,
внешних и внутренних сил, действующих
на i -ую материальную точку.
![]() -
главный вектор всех внешних сил,
действующего на систему материальных
точек, j - номер
j- ой внешней
силы.
-
главный вектор всех внешних сил,
действующего на систему материальных
точек, j - номер
j- ой внешней
силы.
168.
Записав уравнение (167) в проекциях на
оси декартовой системы координат
получим дифференциальные уравнения
движения центра масс:
![]()
169.
Количество движения системы
материальных точек - вектор, равный
геометрической сумме (главному
вектору) количеств движения всех
материальных точек этой системы:
![]() где
где
![]() - скорость движения центра масс.
- скорость движения центра масс.
170. Производная
от количества движения системы
материальных точек по времени равна
главному вектору внешних сил,
действующих на все точки этой системы:
![]() .
.
171. Записав уравнение (167) в проекциях на оси декартовой системы координат, получим:
![]()
![]()
![]()
Уравнения (168) и (169) - дифференциальные (векторная и аналитическая) формы записи теоремы об изменении количества движения системы материальных точек (механической системы).
172. В случае,
когда
![]() или, например
или, например
![]() ,
уравнения (168) и (169) называют законом
сохранения количества движения системы
материальных точек в целом
,
уравнения (168) и (169) называют законом
сохранения количества движения системы
материальных точек в целом
![]() или
или
![]() - в проекции на ось
- в проекции на ось
![]() в частности.
в частности.
173. В векторной конечной форме теорема
об изменении количества движения
системы материальных точек имеет
вид:
![]() или
или
![]()
174. Записав уравнение (173) в проекциях на оси декартовой системы координат, получим выражение для теоремы об изменении количества движения механической системы в аналитической конечной форме:

175. Кинетический момент (главный момент количеств движения) системы материальных точек относительно центра - вектор, равный геометрической сумме моментов количеств движения всех точек системы, взятых относительно этого центра:
![]()
176. Кинетический момент (главный момент количеств движения) системы материальных точек относительно оси - алгебраическая сумма моментов количеств движения всех точек системы, взятых относительно этой оси:
![]()
177. Производная от кинетического
момента системы материальных точек
относительно центра по времени
равна равна главному моменту всех
внешних сил, действующих на все
точки этой системы, относительно того
же центра:
![]()
178. Записав уравнение (177) в проекциях на оси декартовой системы координат, получим:

Уравнения (177) и (178) - теорема об изменении кинетического момента системы материальных точек, записанная в дифференциальной векторной и аналитической формах соответственно.
179. В
случае, когда
![]() или, например,
или, например,
![]() , уравнения (177) и (178), называются законом
сохранения кинетического момента
системы материальных точек относительно
центра (
, уравнения (177) и (178), называются законом
сохранения кинетического момента
системы материальных точек относительно
центра (![]() )
или - оси (
)
или - оси (![]() ).
).
180. Кинетическая
энергия механической системы -
сумма кинетических энергий всех ее
частей (точек, тел):
![]() .
.
Формулы для вычисления кинетической энергии тела (для основных видов движения тел) приведены в таблице.
181.
Приращение кинетической энергии
механической системы на некотором ее
перемещении равно сумме работ всех
внешних сил, действующих на все
точки (тела) этой системы, на данном
перемещении:
![]() ,
где
,
где
![]() - кинетическая энергия системы в
конечном и начальном положениях.
- кинетическая энергия системы в
конечном и начальном положениях.
Формулы для вычисления кинетической энергии тела (для основных видов движения тел) приведены в таблице.
182. Принцип Даламбера для несвободной
механической системы - движущаяся
несвободная механическая система может
рассматриваться как покоящаяся под
действием внешних активных
(задаваемых) сил, реакций внешних
связей и сил инерции. Условия
такого псевдопокоя - равенство нулю
суммы главных векторов всех этих сил
![]() и суммы главных моментов этих сил
относительно любого центра:
и суммы главных моментов этих сил
относительно любого центра:
![]()
183. Аналогично формулируется и записывается принцип Даламбера для свободной механической системы, но естественно без реакций внешних связей и их моментов, т.е.
![]()
![]()
При решении задач уравнения (182) и (183) записываются в аналитической форме, т.е. в проекциях на оси декартовой или естественной системы координат.
184. Абсолютно твердое тело как система материальных точек - неизменяемая система бесконечно большого числа элементарных частиц (материальных точек), бесконечно малое расстояние между которыми всегда неизменно.
185. Масса
твердого тела как системы материальных
точек - предельное значение суммы масс
ее элементарных частиц:
![]() О массе и моменте инерции тела (точки),
как мерах инерции см. п.126 - 129.
О массе и моменте инерции тела (точки),
как мерах инерции см. п.126 - 129.
186. Радиус
инерции тела - расстояние
![]() от оси вращения
до точки, в которую должна быть
сосредоточенна вся масса m
тела, чтобы момент инерции этой
материальной точки относительно этой
оси равнялся моменту инерции тела
относительно этой же оси:
от оси вращения
до точки, в которую должна быть
сосредоточенна вся масса m
тела, чтобы момент инерции этой
материальной точки относительно этой
оси равнялся моменту инерции тела
относительно этой же оси:
![]()
187.
Момент инерции тела
![]() относительно какой-либо оси
относительно какой-либо оси
![]() равен сумме момента инерции
равен сумме момента инерции
![]() тела относительно оси
тела относительно оси
![]() ,
проходящей через центр масс тела, и
параллельной оси
,
и произведения массы
тела на квадрат кратчайшего расстояния
,
проходящей через центр масс тела, и
параллельной оси
,
и произведения массы
тела на квадрат кратчайшего расстояния
![]() между осями:
между осями:
![]() - теорема о моментах инерции тела
относительно параллельных осей.
- теорема о моментах инерции тела
относительно параллельных осей.
Решение ряда задач динамики механической системы, состоящей из твердых тел, предполагает приведение системы сил инерции, действующих на все частицы каждого тела, к центру масс каждого тела (или другому центру приведения, если это целесообразно).
188. В результате
приведения сил инерции к центру, как
правило к центру масс, система бесконечно
большого числа элементарных сил инерции,
действующих на все частицы тела,
заменяется, в общем случае, одной
силой, равной главному вектору сил
инерции
![]() и приложенной в центре приведения
(например в центре масс), и одной парой
сил, с векторным моментом, равным
главному моменту сил инерции, взятому
относительно выбранного центра
приведения:
и приложенной в центре приведения
(например в центре масс), и одной парой
сил, с векторным моментом, равным
главному моменту сил инерции, взятому
относительно выбранного центра
приведения:
![]()
Аналитически многие задачи динамики, а также и статики механической системы изящно (не взирая на степень их сложности) решаются методами аналитической механики. В аналитической механике исходными понятиями являются: степень свободы, обобщенная координата, возможное перемещение, обобщенная скорость, обобщенная сила.
189. Обобщенные координаты - независимые величины, заданием которых однозначно определяется положение всех точек механической системы. Для голономной несвободной механической системы число обобщенных координат равно числу степеней свободы.
Подавляющее число механизмов, используемых в технике, является системами с одной степенью свободы, например: рычаг, лебедка, кривошипно-шатунный механизм, планетарный механизм, тело, вращающееся вокруг неподвижной оси и т.п. Две степени свободы имеет центробежный регулятор. Три степени свободы имеет: свободная материальная точка; несвободное сферически движущееся тело; тело, совершающее плоское движение. Шесть степеней свободы (наибольшее число степеней свободы) имеет свободное твердое тело в общем случае его движения.
190. Голономная несвободная механическая система - несвободная механическая система, перемещение которой в пространстве ограничено голономными (интегрируемыми) связями.
191. Голономная интегрируемая связь - связь, описываемая уравнениями в конечной форме или интегрируемыми дифференциальными уравнениями.
192. Возможные (виртуальные) перемещения - воображаемые элементарные (линейные или угловые, например: ) перемещения точек тела (тел) механической системы), в действительности допускаемые связями, ограничивающими перемещение тела (тел) в пространстве (рисунок 24б).
Для стационарной (с постоянными по времени связями) механической системы действительные перемещения входят в число ее возможных перемещений, т.е. являются их частными случаями.
193. Идеальная
связь - связь, для которой сумма работ
реакций этой связи на возможных
перемещениях точек их приложения равна
нулю:
![]() Например, абсолютно гладкая
поверхность, шероховатая поверхность
в случае качения без скольжения.
Например, абсолютно гладкая
поверхность, шероховатая поверхность
в случае качения без скольжения.
194. Абсолютно гладкая поверхность - научная абстракция, модель, которой заменяется реальная шероховатая поверхность, в результате чего не принимается во внимание трение.
В действительности все поверхности трения достаточно шероховаты и трение имеет место даже при наличии смазки поверхностей трения. В связи с этим силу трения - касательную составляющую полной реакции поверхности как связи - переносят в группу активных (задаваемых) сил, делая тем самым связь условно идеальной, что позволяет применять для решения ряда задач принцип возможных перемещений.
Принцип возможных (виртуальных) перемещений
195. В случае покоя (равновесия) несвободной механической системы (общее уравнение статики)
Для несвободной механической системы со стационарными двухсторонними идеальными связями, находящейся в покое (равновесии), сумма работ всех внешних активных (задаваемых) сил на любом возможном перемещении ее из рассматриваемого положения равна нулю:
![]() или
или
![]()
196. В случае движения несвободной механической системы (общее уравнение динамики)
Для несвободной механической системы со стационарными двухсторонними связями в любой момент времени сумма работ всех активных (задаваемых) сил и сил инерции на любом возможном перемещении ее из рассматриваемого положения равна нулю:
![]()
или
![]()
Для механической системы с одной степенью свободы достаточно записать и решить одно уравнение (195) или (196). Если же система имеет несколько степеней свободы, то уравнение (195) или (196) записывают для каждого независимого перемещения в отдельности. Таким образом, записывается и решается совместно столько уравнений (195) или (196) сколько степеней свободы имеет рассматриваемая механическая система.
197. Колебательное движение материальной точки - движение осуществляемое под действием системы сил, непременно включающей восстанавливающую силу (см. рисунок 25).
II
I

198. Восстанавливающая сила - сила
![]() ,
стремящаяся вернуть материальную точку
в положение равновесия (см. рис. 25).
,
стремящаяся вернуть материальную точку
в положение равновесия (см. рис. 25).
1 99.
Возмущающая сила - сила
99.
Возмущающая сила - сила
![]() периодически
действующая на материальную точку и
поддерживающая ее колебательное
движение (см. рис. 26).
периодически
действующая на материальную точку и
поддерживающая ее колебательное
движение (см. рис. 26).
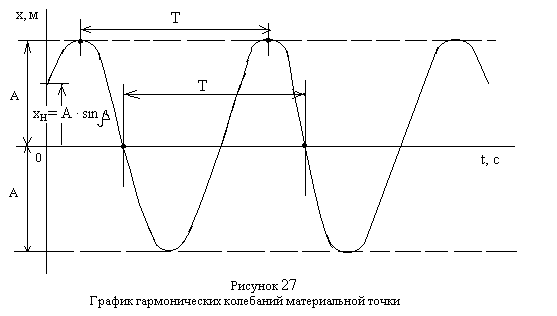
200. Координата
материальной точки (см. рис. 26), совершающей
свободные колебания под действием
линейно изменяющейся восстанавливающей
силы
![]() ,
где
,
где
![]() - …[H/м] - коэффициент
жесткости линейно деформирующейся
(периодически растягивающейся и
сокращающейся вдоль оси 0х абсцисс
) пружины] изменяется по
закону
- …[H/м] - коэффициент
жесткости линейно деформирующейся
(периодически растягивающейся и
сокращающейся вдоль оси 0х абсцисс
) пружины] изменяется по
закону
![]() ,
[ м ] - уравнение
гармонических колебаний материальной
точки.
,
[ м ] - уравнение
гармонических колебаний материальной
точки.
201. Амплитуда
 свободных
колебаний материальной точки
- максимальное удаление (отклонение)
материальной точки от положения 0
равновесия в крайнее левое В
или крайнее правое D
положения, где
свободных
колебаний материальной точки
- максимальное удаление (отклонение)
материальной точки от положения 0
равновесия в крайнее левое В
или крайнее правое D
положения, где
![]() и
и
![]() - начальная координата и проекции
начальной скорости движения материальной
точки;
- начальная координата и проекции
начальной скорости движения материальной
точки;
![]() ,
[c-1]
- циклическая частота свободных
колебаний материальной точки;
,
[c-1]
- циклическая частота свободных
колебаний материальной точки;
![]() -
начальная
фаза колебаний,
-
начальная
фаза колебаний,
![]() .
.
202. В диапазоне
![]() значений угла
каждому значению
значений угла
каждому значению
![]() соответствует два значения угла. Поэтому
необходимо знать значения
соответствует два значения угла. Поэтому
необходимо знать значения
![]() и
и
![]() .
.
203.
Период
![]() свободных
колебаний - интервал времени в течении
которого совершается одно колебание,
т.е. время, за которое точка возвращается,
например, в крайнее правое положение
D, или
свободных
колебаний - интервал времени в течении
которого совершается одно колебание,
т.е. время, за которое точка возвращается,
например, в крайнее правое положение
D, или![]() - промежуток времени между двумя
последовательными прохождениями точки
в одном направлении через какое-либо
фиксированное положение, например
положение 0 равновесия (см. рис. 27)
- промежуток времени между двумя
последовательными прохождениями точки
в одном направлении через какое-либо
фиксированное положение, например
положение 0 равновесия (см. рис. 27)

 204.
Координата
материальной
точки (см. рис. 28), совершающей затухающие
колебания под действием линейно
изменяющиеся восстанавливающей силы
204.
Координата
материальной
точки (см. рис. 28), совершающей затухающие
колебания под действием линейно
изменяющиеся восстанавливающей силы
![]() при линейном законе сопротивления
движению
при линейном законе сопротивления
движению
![]() , изменяется по закону
, изменяется по закону
![]() ,
[ м ] - уравнение
свободных затухающих колебаний.
,
[ м ] - уравнение
свободных затухающих колебаний.
205.
- 1 константа (как и величина
![]() )
интегрирования дифференциального
уравнения затухающих колебаний, -2
гипотетическое… максимальное отклонение
)
интегрирования дифференциального
уравнения затухающих колебаний, -2
гипотетическое… максимальное отклонение
![]() материальной
точки от положения равновесия равное
материальной
точки от положения равновесия равное
![]() ,
при
,
при
![]() с,
т.е. в начальные момент времени (см. рис.
28).
с,
т.е. в начальные момент времени (см. рис.
28).
206.
![]() -
частота свободных затухающих колебаний
материальной точки, где
-
частота свободных затухающих колебаний
материальной точки, где
![]() [c-1]
- коэффициент затухания свободных
колебаний материальной точки.
[c-1]
- коэффициент затухания свободных
колебаний материальной точки.
207.
![]() , т.к. в диапазоне
, т.к. в диапазоне
![]() значений угла
(начальной фазы затухающих колебаний)
каждому значению
значений угла
(начальной фазы затухающих колебаний)
каждому значению
![]() соответствует два значения угла,
необходимо знать значения
соответствует два значения угла,
необходимо знать значения
![]() и
и
![]() .
.
 208.
208.
 - период свободных затухающих колебаний
- промежуток времени между двумя
последовательными прохождениями
материальной точки в одном направлении
через положение равновесия.
- период свободных затухающих колебаний
- промежуток времени между двумя
последовательными прохождениями
материальной точки в одном направлении
через положение равновесия.
209. Реальная
(действительная) амплитуда свободных
затухающих колебаний величина переменная
…
![]() и
т.д.
и
т.д.![]() см.
рис. 30 - наибольшее отклонение
см.
рис. 30 - наибольшее отклонение![]() в ту или другую сторону от положения
равновесия в течении каждого колебания.
в ту или другую сторону от положения
равновесия в течении каждого колебания.
210. Последовательные значения переменной - амплитуды затухающих колебаний образуют ряд
![]()
211. Отношение
последовательных членов
![]() и
ряда
к
соответствующим моментам времени
и
ряда
к
соответствующим моментам времени
![]() и
и
![]() ,
см. рис. 30 равно:
,
см. рис. 30 равно:

 -
отвлеченное число, так называемый
декремент затухающих колебаний -
const для данного ряда
последовательных значений амплитуды
(значений параметров затухающих
колебаний).
-
отвлеченное число, так называемый
декремент затухающих колебаний -
const для данного ряда
последовательных значений амплитуды
(значений параметров затухающих
колебаний).
![]()
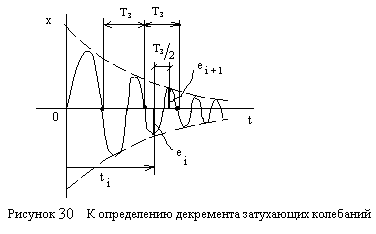 - логарифмический
декремент затухающих колебаний.
- логарифмический
декремент затухающих колебаний.
![]()
212. Апериодическое
движение материальной точки - движение
материальной точки под действием
восстанавливающей силы при
значительном сопротивлении движению,
когда
![]() ,
устраняющем колебательный характер
движения.
,
устраняющем колебательный характер
движения.
Уравнение
апериодического движения при
![]()
![]() содержит гиперболический синус
аргумента
содержит гиперболический синус
аргумента
![]() ,
где
,
где
![]() и
и
![]() -
константы интегрирования дифференциального
уравнения затухающих колебаний при
,
-
константы интегрирования дифференциального
уравнения затухающих колебаний при
,
![]() - некоторая константа. В таком случае
- некоторая константа. В таком случае
![]() графики апериодического движения имеют
вид:
графики апериодического движения имеют
вид:
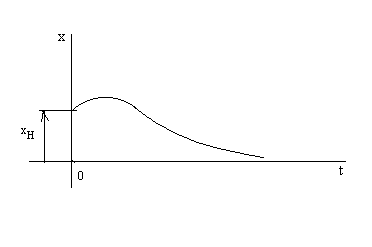
а) при начальном
движении
![]() материальной точки в направлении
отсчета положительных значений координаты
,
когда скорость достаточно велика;
материальной точки в направлении
отсчета положительных значений координаты
,
когда скорость достаточно велика;
б) при начальном
движении в направлении отсчета
отрицательных значений координаты
,
когда начальная скорость
![]() достаточно велика;
достаточно велика;
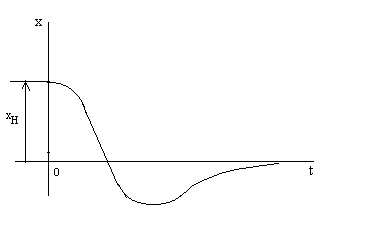
в )
при начальном движении в направлении
отсчета отрицательных значений координаты
,
когда начальная скорость
невелика;
)
при начальном движении в направлении
отсчета отрицательных значений координаты
,
когда начальная скорость
невелика;
213. Уравнение
апериодического движения материальной
точки при
![]() имеет вид:
имеет вид:
![]() .
.
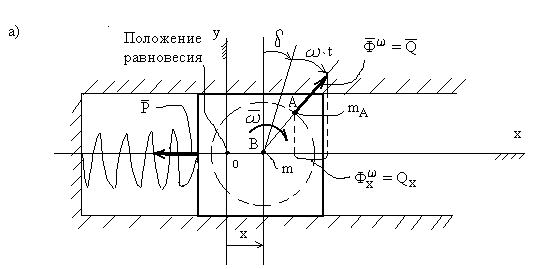
214. Практически
наиболее важным является гармонический
закон
![]() изменения возмущающей силы
,
см. рисунок 32.
изменения возмущающей силы
,
см. рисунок 32.
215. Параметры гармонически изменяющейся возмущающей силы:
![]() - амплитуда возмущающей силы наибольшее
- амплитуда возмущающей силы наибольшее
![]() значение
модуля
значение
модуля
![]() возмущающей силы
,
[ Н ] ;
возмущающей силы
,
[ Н ] ;
![]() -
частота изменения возмущающей силы, [
с-1 ] - число
полных циклов изменения возмущающей
силы за
-
частота изменения возмущающей силы, [
с-1 ] - число
полных циклов изменения возмущающей
силы за![]() секунд;
секунд;
![]() - фаза изменения возмущающей силы,
[рад], [
];
- фаза изменения возмущающей силы,
[рад], [
];
![]() -
начальная фаза изменения возмущающей
силы, [рад], [
];
-
начальная фаза изменения возмущающей
силы, [рад], [
];
![]() - период изменения возмущающей силы, [
c ].
- период изменения возмущающей силы, [
c ].
Например:
![]() ,
,
![]() ,
где
,
где
![]() -
модуль центробежной силы,
-
модуль центробежной силы,
![]() - угловая скорость вращения
несбалансированной массы
- угловая скорость вращения
несбалансированной массы
![]() ,
см. рисунок 32.
,
см. рисунок 32.
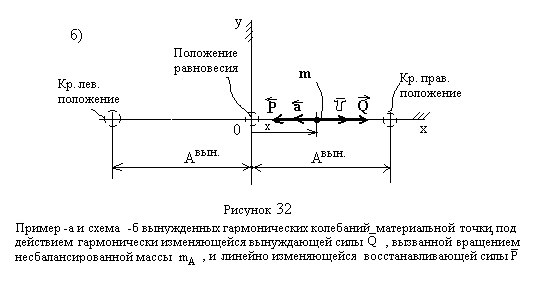
216. Дифференциальное уравнение вынужденных гармонических колебаний:
![]() ,
где
,
где
![]() .
.
Уравнение гармонических вынужденных колебаний малой частоты
![]() где
где
![]() - амплитуда вынужденных гармонических
колебаний малой частоты, когда
- амплитуда вынужденных гармонических
колебаний малой частоты, когда
![]() .
В этом случае материальная точка
отклонена в ту сторону, в которую
направлена в данный момент времени
возмущающая сила
,
см. рис. 32.
.
В этом случае материальная точка
отклонена в ту сторону, в которую
направлена в данный момент времени
возмущающая сила
,
см. рис. 32.
218. Уравнение гармонических вынужденных колебаний большой частоты
![]() где
где
![]() - амплитуда вынужденных гармонических
колебаний большой частоты, когда
- амплитуда вынужденных гармонических
колебаний большой частоты, когда
![]() .
В этом случае отклонение материальной
точки от положения равновесия всегда
противоположно направлению возмущающей
силы
в данный момент времени.
.
В этом случае отклонение материальной
точки от положения равновесия всегда
противоположно направлению возмущающей
силы
в данный момент времени.
Таким образом
вынужденные колебания материальной
точки без учета сопротивления движению
- результирующие вынужденные колебания,
складывающиеся из свободных колебаний
материальной точки под действием
восстанавливающей силы
и собственно вынужденных колебаний под
действием возмущающей силы
,
т.е.
![]() .
.
При
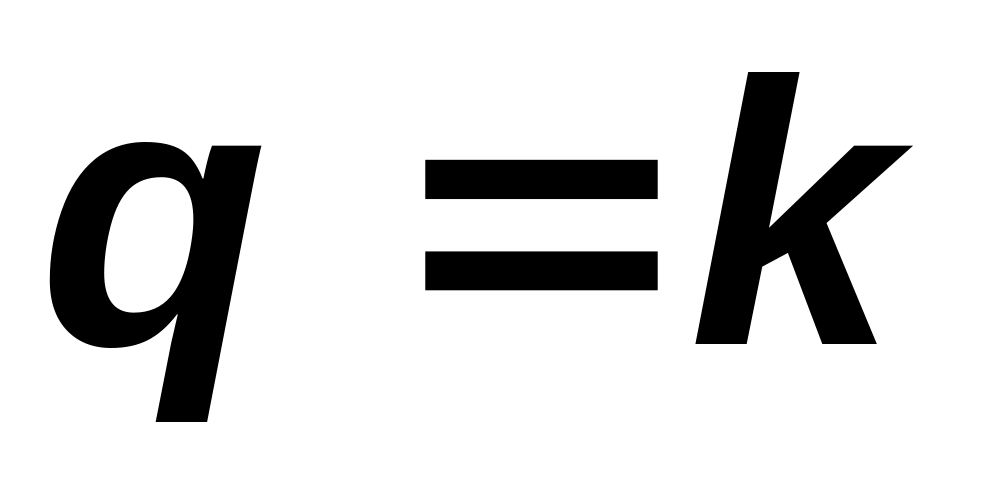
 - явление резонанса,
см. рис. 33.
- явление резонанса,
см. рис. 33.Статистическое отклонение
 материальной точки от положения
равновесия, когда
материальной точки от положения
равновесия, когда
 ,
,
![]() .
.
221. Коэффициент динамичности
![]() равен
равен
 ,
при
,
при
![]() ;
;
 ,
,
при
.
При
![]() и
- явление резонанса, см. рис. 33.
и
- явление резонанса, см. рис. 33.
2 22.
Вынужденные колебания материальной
точки при наличии сопротивления движению,
см. рис. 34 - результирующие колебания,
складывающиеся из затухающих колебаний
материальной точки под действием
восстанавливающей силы
и силы сопротивления движению
(или апериодического движения) и
собственно вынужденных колебаний
материальной точки под действием
возмущающей силы
.
22.
Вынужденные колебания материальной
точки при наличии сопротивления движению,
см. рис. 34 - результирующие колебания,
складывающиеся из затухающих колебаний
материальной точки под действием
восстанавливающей силы
и силы сопротивления движению
(или апериодического движения) и
собственно вынужденных колебаний
материальной точки под действием
возмущающей силы
.
Дифференциальное уравнение таких колебаний
 и его
и его
решения:
при незначительном сопротивлении движению, когда

![]() ;
;
- при значительном сопротивлении движению (апериодическое движение), когда
![]() ;
;
- при значительном сопротивлении движению (апериодическое движение), когда
![]() .
.
224. Амплитуда вынужденных колебаний с учетом сопротивления движению равна:
а) при малых частотах вынужденных колебаний,
![]()
 ;
;
б)
при больших частотах вынужденных
колебаний,
![]()
225. Сдвиг фазы
вынужденных колебаний - угол на
который фаза
![]() вынужденных колебаний меньше (отстает)
от фазы
вынужденных колебаний меньше (отстает)
от фазы
![]() изменения возмущающей силы,
изменения возмущающей силы,
![]() - при вынужденных колебаниях малой
частоты, когда
.
- при вынужденных колебаниях малой
частоты, когда
.
226.
Коэффициент
![]() динамичности
вынужденных колебаний малой частоты
с учетом сопротивления движению равен:
динамичности
вынужденных колебаний малой частоты
с учетом сопротивления движению равен:
 .
.
227. При равенстве (близости)
частот свободных
![]() и
вынужденных
колебаний
материальной точки, т.е. когда
(или
и
вынужденных
колебаний
материальной точки, т.е. когда
(или
![]() )
наступает резонанс - резкий рост амплитуды
вынужденных колебаний, см. рис. 35 .
Сопротивление движению
сдерживает рост амплитуды при наступлении
резонанса.
)
наступает резонанс - резкий рост амплитуды
вынужденных колебаний, см. рис. 35 .
Сопротивление движению
сдерживает рост амплитуды при наступлении
резонанса.
Н а
частоте и периоде результирующих
вынужденных колебаний сопротивление
движению не сказывается, потому
а
частоте и периоде результирующих
вынужденных колебаний сопротивление
движению не сказывается, потому
228.
![]() - период результирующих вынужденных
колебаний, он же период
изменения возмущающей силы, т.е. период
собственно вынужденных колебаний; где
- частота результирующих вынужденных
колебаний, она же частота
изменения возмущающей силы, т.е. частота
собственно вынужденных колебаний.
- период результирующих вынужденных
колебаний, он же период
изменения возмущающей силы, т.е. период
собственно вынужденных колебаний; где
- частота результирующих вынужденных
колебаний, она же частота
изменения возмущающей силы, т.е. частота
собственно вынужденных колебаний.
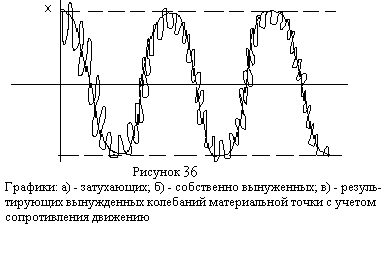
 Графики результирующего вынужденного
колебания материальной точки и его
составляющих колебаний приведены на
рисунке 36.
Графики результирующего вынужденного
колебания материальной точки и его
составляющих колебаний приведены на
рисунке 36.