3 Кинематика

67. Кинематика - раздел теоретической механики, в котором изучается движение материальных тел с геометрической точки зрения, вне связи с силами, определяющими это движение.

Кинематика материальной точки

В кинематике материальной точки решается две основные задачи: определение положения точки в рассматриваемой системе отсчета в определенный момент времени; определение скорости и ускорения в любой момент времени.

Для описания (задания) движения точки в кинематике применяют три способа: векторный, координатный и естественный.

68. Траектория движения точки - геометрическое место последовательных положений движущейся точки в рассматриваемой системе отсчета.

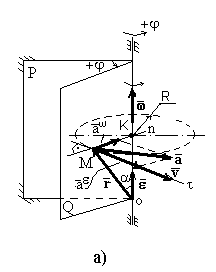
Векторный способ задания движения точки (рисунок - 12а).

69. Уравнение движения точки - вектор-функция времени, т.е. .

70. Скорость движения точки истинная мгновенная - векторная величина, характеризующая быстроту и направление движения точки в рассматриваемой системе отсчета, - векторная производная, как вектор, всегда направлена по касательной к траектории движения точки в данной точке.

71. Ускорение точки истинное мгновенное - векторная величина, характеризующая быстроту изменения модуля скорости и направления движения точки, ; как вектор, всегда расположен в соприкасающейся плоскости.

72. Соприкасающаяся плоскость - плоскость, всегда касательная к траектории, и проходящая через вектор скорости и центр кривизны (ЦК) траектории в данной точке (на рисунке 12а заштрихована).

Координатный способ задания движения точки (рисунок 12а).

73. Уравнения движения точки - алгебраические уравнения вида:

в случае пространственного движения точки;

в случае движения точки на плоскости;

при движении точки по прямой, где - координаты точки в декартовой системе координат.

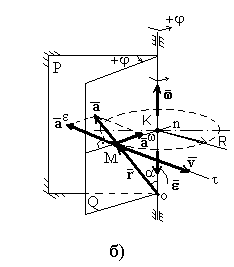
Рисунок 12 - Задание движения векторным и координатным

способами - а; естественным способом - б

74. Уравнение траектории точки - алгебраические уравнения вида: , в случае пространственного движения точки;

в случае движения точки на плоскости ; - при движении точки по прямой линии.

75. Скорость движения точки определяется по ее проекциям на оси декартовой системы координат, , где , .

76. Ускорение точки определяется по его проекциям на оси декартовой системы координат _, где ,

Естественный способ задания движения точки (рисунок 12б)

Движение материальной точки считается заданным (описанным) естественным способом, если известны: траектория движения; уравнение движения; начало отсчета; направление отсчета положительных значений дуговой координаты.

77. Уравнение движения - алгебраическое уравнение вида

где - дуговая координата.

78. Дуговая координата – расстояние, отсчитываемое по траектории движения точки от начала отсчета (НО) до места положения точки на траектории.

79. Начало отсчета - неподвижная точка на траектории, намеченная произвольно, в одном направлении от которой отсчитываются положительные значения дуговой координаты; в другом - отрицательные .

80. Естественная система координат - подвижная система отсчета, представляющая собой совокупность трех взаимно перпендикулярных осей (касательной , нормали и бинормали (на рисунке 1б не показана) к траектории в данной точке) с общим началом (точкой), совмещенным с движущейся материальной точкой. Координатная плоскость , проходящая через касательную и нормаль к траектории в данной точке - соприкасающаяся плоскость, на рисунке 1а заштрихована. При движении точки по траектории естественная система координат движется вместе с ней, при этом ось касательная и соприкасающаяся плоскость всегда остаются касательными к траектории в любой её точке.

81. Скорость движения точки определяется по ее проекции на касательную к траектории в данной точке, , где - орт касательной, .

82. Ускорение точки определяется по его проекциям на касательную и нормаль к траектории в данной точке, , орт нормали, , - радиус кривизны траектории в данной точке.

83. Радиус кривизны - расстояние по нормали к траектории в данной точке от центра кривизны (ЦК) траектории в данной точке до местоположения данной точки на траектории.

84. Кривизна траектории в данной точке - величина обратная радиусу кривизны, .

85. Вектор кривизны - .

86. Длина пути - расстояние, пройденное точкой по траектории от одного положения на ней до другого, 87. Уравнения равнопеременного движения точки - алгебраические уравнения, описывающие изменения скорости и дуговой координаты точки во времени в случае постоянства проекции ускорения точки на касательную , т.е. при где , - начальные скорость и дуговая координата точки в начальный момент времени.

88. Уравнения равномерного движения точки - уравнения, описывающие движение точки, когда , .

Сложное движение точки.

89. Сложное движение точки - движение точки, состоящее из движения ее вместе с некоторым телом и движения ее относительно тела, - абсолютное движение, результирующее двух составляющих его движений, переносного и относительного.

90. Абсолютное движение точки - движение точки относительно системы отсчета связанной с землей.

91. Переносное движение точки - движение точки вместе с телом относительно земли.

92. Относительное движение точки - движение точки относительно системы отсчета, связанной с телом (т.е. движение относительно тела).

93. Абсолютная скорость, ускорение точки - скорость, ускорение ее абсолютного движения.

94. Переносная скорость, ускорение точки - скорость, ускорение в движении относительно земли той точки тела, в которой в данный момент времени находится рассматриваемая материальная точка.

95. Относительная скорость, ускорение точки - скорость, ускорение относительного движения точки.

96. Абсолютная скорость точки равна геометрической сумме переносной и относительной скоростей:

97. Абсолютное ускорение точки равно геометрической сумме переносного, относительного и кориолисового ускорений:

98. Кориолисово ускорение (ускорение Кориолиса) - составляющая абсолютного ускорения точки, характеризующая влияние относительного движения на модуль и направление переносной скорости и влияние переносного движения на направление относительной скорости точки, равная удвоенному векторному произведению вектора угловой скорости переносного вращения на вектор относительной скорости точки:

(см. рисунок 16б).

Кинематика твердого тела

В теоретической механике различают следующие основные виды движения твердых тел: поступательное, вращательное, плоскопараллельное (плоское), сферическое, сложное движение в общем случае.

99. Поступательное движение твердого тела - движение, при котором любая прямая, соединяющая две любые точки тела, движется параллельно самой себе, при этом скорости всех точек тела и их ускорения геометрически равны, т.е. , для всех точек тела в данный момент времени, в данном положении твердого тела. Траектории описываемые всеми точками тела – геометрически подобны.

100. Вращательное движение (движение вокруг неподвижной оси) - движение твердого тела, при котором остаются неподвижными все точки тела, лежащие на некоторой прямой, называемой осью вращения, а все другие точки движутся в плоскостях, перпендикулярных оси вращения и описывают в этих плоскостях окружности, центры которых лежат на оси вращения.

101. Ось вращения - геометрическое место неподвижных точек тела, образующих неподвижную материальную прямую.

102. Уравнение вращения - уравнения вида описывающее изменение угла поворота тела (угловой координаты) с течением времени. Угол поворота и число оборотов тела, соответствующее ему, связаны уравнением .

103. Угол поворота (угловая координата) - двугранный угол, образованный полуплоскостями, проходящими через ось вращения, одна из которых неподвижна, а другая вращается вокруг оси вместе с телом. В одном направлении вокруг оси отсчитываются положительные значения угла , в другом - отрицательные (рисунок 13).

104. Угловая скорость вращения - 1) алгебраическая величина , характеризующая быстроту изменения угла поворота с течением времени и направление вращения, и равная ; - 2) вектор , направленный по оси вращения в ту сторону, откуда видно вращение тела в направлении противоположном вращению часовой стрелки. Если , то вращение в направлении отсчета положительных значений угла поворота, если , то - в направлении отрицательных значений , см. рисунок 13.

Рисунок 13 - Вращение тела ускоренное а; замедленное - б

105. Угловое ускорение – 1) алгебраическая величина , характеризующая быстроту изменения угловой скорости с течением времени, и равная ; 2) вектор , направленный по оси вращения в сторону вектора при ускоренном вращении (рисунок 13а), - в противоположную сторону при замедленном (рисунок 13б). Вращение ускоренное, если и или и , т.е. когда знаки первой и второй производных по времени от угла поворота совпадают; - замедленное, если , а или , и т.е., когда знаки производных противоположны.

106. Уравнения равнопеременного вращения - уравнения вида: описывающие изменение угловой скорости и угла поворота с течением времени , когда , где - начальные угловая скорость и угол поворота тела в начальный момент времени .

107. Уравнение равномерного вращения - уравнение , описывающее вращение тела, когда , .

108. Вращательная (окружная, линейная) скорость точки твердого тела - скорость движения данной точки тела по окружности, описываемой ею в плоскости перпендикулярной оси вращения с центром K вращения лежащим на этой оси, , где - радиус вращения точки (окружности описываемой точкой при вращении тела). Как вектор, вращательная скорость точки тела всегда направлена по касательной к описываемой ею окружности в направлении вращения тела, см. рисунок 13.

109. Вращательное ускорение точки тела - 1) алгебраическая величина, равная , и характеризующая изменение величины вращательной скорости данной точки; - 2) вектор , направленный по той же касательной к описываемой точкой окружности, по которой направлен вектор вращательной скорости, где - радиус-вектор данной точки относительно любого неподвижного центра (например точка О), расположенного на оси вращения. При ускоренном вращении направления векторов и совпадают (рисунок 13а), при замедленном - противоположны (рисунок 13б).

110. Центростремительное ускорение точки тела – 1) величина, характеризующая темп изменения направления вращательной скорости точки с течением времени, и равная ; - 2) вектор , направленный всегда от точки к центру К вращения; всегда положительный скаляр.

111. Полное (линейное, окружное) ускорение точки тела - вектор, равный , вращательная и центростремительная составляющие которого всегда перпендикулярны, т.е.  , а модуль , и характеризующий быстроту изменения вектора вращательной скорости и по величине, и по направлению.

112. Плоскопараллельное (плоское) движение тела - движение, при котором каждая точка тела движется в плоскости, параллельной некоторой неподвижной плоскости (рисунок 3а) при этом: а) плоская фигура, образованная сечением тела этой неподвижной плоскостью Q , во все время движения тела остается в этой неподвижной плоскости; б) при движении тела отрезок M₁MM₂ , перпендикулярный к этой неподвижной плоскости Q, остается параллельным своему начальному положению; в) все точки тела, лежащие на этом отрезке M₁MM₂ , перпендикулярном плоскости Q, описывают тождественные параллельные между собой траектории и в каждый момент времени имеют геометрически равные скорости и ускорения, то есть ; для всех точек данного отрезка M₁MM₂ в данный момент времени, в данном положении твердого тела (см. рисунок 14а).

113. Уравнения плоского движения - уравнения вида: , , , где , - координаты полюса, - угол поворота плоской фигуры вокруг полюса, описывающие плоское движение, как сложное результирующее двух составляющих его движений, поступательного движения плоской фигуры вместе с полюсом и вращательного движения плоской фигуры в плоскости ее движения вокруг полюса, см. рисунок 14б.

Рисунок 14 - К определению: плоского движения - а; уравнений движения - б

114. Полюс - любая точка плоской фигуры, например точка С (на рисунке 14б), движение которой задано , , или может быть определено.

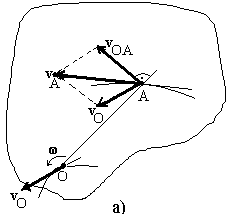
115. Скорость любой точки, например А, плоской фигуры равна геометрической сумме скорости полюса (точка О на рисунке 15) и вращательной скорости этой точки А во вращении вместе с плоской фигурой вокруг полюса - , где (рисунок 15а).

116. Ускорение любой точки, например А, плоской фигуры равно геометрической сумме ускорения полюса и ускорения этой точки во вращении вместе с плоской фигурой вокруг полюса , где , , , см. рисунок 15б.

117. Мгновенный центр скоростей - точка плоской фигуры, скорость которой в данный момент времени равна нулю. Для разных моментов времени мгновенным центром скоростей являются разные точки плоской фигуры.

118. Мгновенный центр ускорений - точка плоской фигуры, ускорение которой в данный момент времени равно нулю. Для разных моментов времени мгновенным центром ускорений являются разные точки плоской фигуры.

Для данного момента времени мгновенный центр скоростей и ускорений - разные точки плоской фигуры.

Р исунок 15 - Определение скорости - а и ускорения - б точки

плоской фигуры

119. Сферическое движение тела - движение, при котором одна из точек тела во все время движения остается неподвижной, а все остальные точки движутся по сферическим поверхностям, центры которых совпадают с неподвижной точкой, например О, (рисунок 16а).

Рисунок 16 - К определению сферического движения - а; направление ускорения Кориолиса - б

120. Уравнения сферического движения - уравнения вида: где - эйлеровы углы (углы прецессии, нутации и собственного вращения), см. рисунок 16а.

Сферическое движение в фиксированный момент времени можно рассматривать как простое вращение вокруг так называемой мгновенной оси.

121. Мгновенная ось вращения - подвижная ось, проходящая неизменно через неподвижную точку О, геометрическое место последовательных положений точек твердого тела, скорости которых в данный момент времени равны нулю..

122. Вектор угловой скорости сферически движущегося твердого тела в данный момент времени направлен по мгновенной оси вращения в ту сторону, смотря откуда поворот тела вокруг мгновенной оси виден в направлении противоположном вращению часовой стрелки, если смотреть с вершины мгновенной оси.

123. Вектор углового ускорения сферически движущегося твердого тела в данный момент времени направлен по оси углового ускорения при ускоренном вращении в ту же сторону, что и , при замедленном - в обратную сторону и равен , см. рис. 17б.

124. Скорость (вращательная, линейная, окружная) - какой либо точки сферически движущегося твердого тела равна , модуль , где - кратчайшее расстояние от точки до мгновенной оси вращения, см. рис.17а.

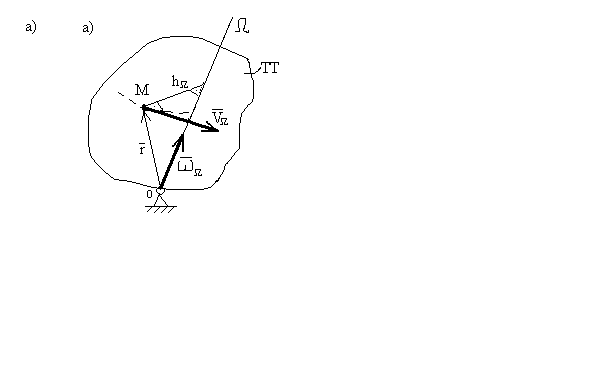
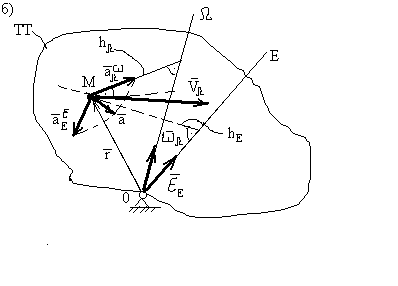
Рисунок 17 К определению скорости - а) и ускорения - б) точки сферически движущегося твердого тела.

125. Ускорение точки сферически движущегося твердого тела определяется геометрическим суммированием вращательной и осестремительной составляющей ; ; ; , см. рис. 17 б.

126. Сложное движение тела в общем случае - результирующее двух составляющих его движений: поступательного движения тела вместе с полюсом и сферического движения тела вокруг полюса.

127. Уравнения сложного движения тела в общем случае - уравнения вида:

, , , ,

где - координаты полюса.

128. Скорость любой точки свободного твердого тела, совершающего сложное движение в общем случае, равно геометрической сумме скорости полюса и скорости этой точки в ее сферическом движении вместе с телом вокруг ее полюса

129. Ускорение любой точки свободного твердого тела, совершающего сложное движение в общем случае, равна геометрической сумме ускорений полюса , вращательного и осестремительного ускорений этой точки в ее сферическом движении вместе с телом вокруг полюса .

За полюс может быть выбрана любая точка тела, движение которой известно или может быть определено.