
- •Найти коэффициент а.
- •Найти функцию распределения системы (X,y) и компонент X и y.
- •Найти плотность и функцию распределения системы (X,y)
- •Найти плотности распределения системы (X,y) и компонент X и y.
- •Вычислить корреляционный момент k(X,y)
- •Установить, зависимы ли X и y.
- •Найти коэффициент а.
- •II. Основные теоретические положения и их применение к решению типовых задач.
- •2.2. Одномерная случайная величина, ее функция распределения.
- •2.3. Дискретные случайные величины
- •2.4. Непрерывные случайные величины.
- •2.5. Числовые характеристики случайных величин.
2.4. Непрерывные случайные величины.
Вторым наиболее важным классом СВ является класс непрерывных СВ – таких СВ, для которых их ф.р. в каждой точке х может быть представлена в виде
F(x)= (2.6.)
(2.6.)
Где f(y) – некоторая неотрицательная функция, называемая плотностью распределения вероятностей.
Из
определения (2.6) следует непрерывность
ф.р. F(x)
для непрерывной СВ. Для построения
математической модели эксперимента с
непрерывной СВ можно задать на множестве
возможных значений
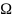 x
либо ф.р.
F(X)
либо плотность распределения f(x).
Например, вероятность попадания СВ Х в
интервал (x1,
x2)
вычисляется по формуле :
x
либо ф.р.
F(X)
либо плотность распределения f(x).
Например, вероятность попадания СВ Х в
интервал (x1,
x2)
вычисляется по формуле :
P{x1≤X≤x2}=F(x2)-F(x1)= (2.7)
Из формулы (2.6) и свойств плотности распределения ,приведенных в таблице 2.1 следует,что множество возможных значений Ωx непрерывной СВ несчетно, вероятность каждого значения равна нулю. Поэтому вероятности P(x1<X<x2), P(x1<X≤x2), P(x1≤X≤x2) также вычисляются по формуле(2/7).
Геометрически вероятность попадания СВ в интервал (a,b) равна площади криволинейной трапеции, ограниченной плотностью распределения, осью Ox и прямыми x=a, x=b.
Пример 2.4. Непрерывная СВ Х залана функцией распределения
F(x)=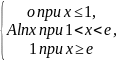 (2.8)
(2.8)
Найти: 1) значение коэффициента А. 2) Плотность распределения f(x). 3) вероятность попадания СВ Х в интервал (1.2)
Решение:
Коэффициент А находим , используя непрерывность функции F(x):
1=F(e)=limF(x)=Alne=А ,откуда А=1.
Чтобы найти плотность распределения f(x) продифференцируем ф.р. F(x) по x (третье свойство плотности распределения – см. таблицу 2.1):
f(x)=F’(x)=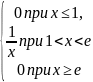 (2.9)
(2.9)
Вероятность того, что СВ Х примет значение из интервала(1.2), равна определенному интегралу от плотности распределения в пределах от 1 до 2 :
P(1<X<2)=
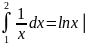 12=
ln2
12=
ln2
2.5. Числовые характеристики случайных величин.
Наиболее важными числовыми характеристиками СВ являются математическое ожидание (м.о.) , дисперсия, среднеквадратическое отклонение и моменты различных порядков.
Математическое
ожидание МХ дискретной СВ Х, принимающей
значения pi
с вероятностью xi
i=1,2,///,
определяется как сумма ряда МХ=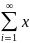 ipi
при условии, что ряд этот абсолютно
сходится(в противном случае говорят,
что м.о. не существует). Если СВ Х принимает
лишь конечное число значений xi,…xn,
то
ipi
при условии, что ряд этот абсолютно
сходится(в противном случае говорят,
что м.о. не существует). Если СВ Х принимает
лишь конечное число значений xi,…xn,
то
МХ=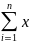 ipi
(2.11)
ipi
(2.11)
Математическое ожидание указывает среднее значение СВ Х, около которого происходит разброс наблюдаемых значений СВ Х.
Для непрерывной СВ суммирование в (2.1.) заменяется интегрированием , и м.о. определяется как интеграл
МХ= (2.12)
(если этот интеграл абсолютно сходится)
Дисперсией СВ Х называется математическое ожидание квадрата отклонения случайно величины от ее математического ожидания :
DX=M(X-MX)2 (2.13)
Дисперсия есть мера рассеяния значений СВ около ее м.о.
Пример 2.5. Найти математическое ожидание и дисперсию СВ Х, определенной в примере 2.2.
Решение. Зная ряд распределения МХ и DX находим по формулам (2.11) и (2.13)
MX=0+1*0.398+2*0.092+3*0.006=0.6;
DX=1*0.398+22*0.092+32*0.006-0.62=0.46.
Пример 2.6. Физиками экспериментально доказано, что для радиоактивных веществ время жизни атома Х- случайная величина, распределенная по показательному закону
P(X<t)=1-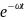 где
где
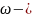 постоянная, называемая «вероятностью
распада» и характеризующая данный тип
атомов.
постоянная, называемая «вероятностью
распада» и характеризующая данный тип
атомов.
Найти
1) среднее время жизни атома t
и разброс около среднего 2) вероятность
того, что атом распадется за время,
меньшее t
; за время от t
до 2t
3) доказать, что радиоактивные атомы «не
стареют» : если известно, что атом не
распался до момента
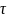 ,
т.е. Х>
, то вероятность прожить еще время, не
меньшее t
, определяется :
,
т.е. Х>
, то вероятность прожить еще время, не
меньшее t
, определяется :
P(X>t+ /X> )=
Решение. 1) Для нахождения числовых характеристик СВ сначала надо найти плотность распределения f(x) как производную от ф.р. (при t≥o)
F(t)
=P(X<t)=1-P(X≥t)=1-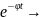 f(t)=F’(t)=
f(t)=F’(t)=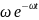 ,
так как СВ Х принимает только положительные
значения, то при t<0
F(t)=0,
f(t)=o,
и в формулах для MX
DX
интегрирование фактически проводится
по интервалу (0,
,
так как СВ Х принимает только положительные
значения, то при t<0
F(t)=0,
f(t)=o,
и в формулах для MX
DX
интегрирование фактически проводится
по интервалу (0,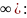
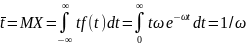 ,
(2.14)
,
(2.14)
DX=MX2-(MX)2=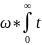 2
dt-
1/
2=1/
2
2
dt-
1/
2=1/
2
Вероятность того , что СВ Х примет значение из интервала [a,b), есть F(b)-F(a)/ Поэтому
P(X<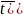 =F(
=F(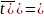 1-
,
P(
1-
,
P(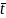 <X<2
)=
F(2
)-
F(
<X<2
)=
F(2
)-
F(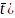 .
.
Заменяя в соответствии с (1.14) в этих фолрмулах на 1/ , получаем:
P(X<t)=1-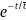 =1-1/e
0.63,
=1-1/e
0.63,
P(
<X<2
)=
1-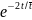 -(1-e-1)
-(1-e-1)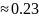
В соответствии с законом больших чисел это означает, что за время, меньшее
Распадается около 63% атомов, имевшихся в начальный момент, за время от до
2 - 23% атомов, за время, большее 2 - 14% атомов.
По определению условной вероятности P(A/B)=P(AB)/P(B)/ Поэтому
P(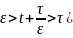 =P(
=P(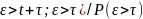 =P(
=P(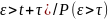 =
=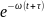 /
=
/
=
Пример
2.7. СВ Х имеет плотность распределения
f(x)={A-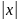 при
при
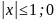 при
>1.
при
>1.
Требуется 1)найти постоянный параметр А и функцию распределения F(x) 2) вычислить P(X>0.5) 3) Найти MX и DX/
Решение. Представим f(x) в следующем виде:
f(x)=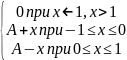
Для нахождения параметра А воспользуемся третьим свойством плотности распределения, согласно которому
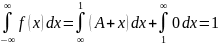
Отсюда получаем А=1. Значение параметра подставляем в формулу плотности распределения и находим функцию распределения по ее определению:
F(x)=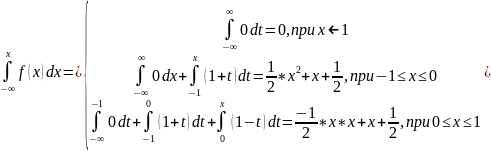
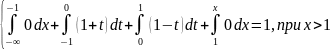
Вероятность P(X>1/2) можно вычислить по четвертому свойству плотности распределения:
P(X>1/2)=P(1/2<X<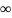 )=
)=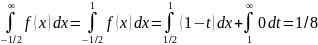
Или еще проще, через функцию распределения:
P(X>1/2)=P(1/2<X<1)=F(1)-(1/2)=1-7/8=1/8
Математическое ожидание MX и дисперсия DX непрерывной СВ Х определяется с помощью плотности распределения по формулам из табл. 2.1:
MX=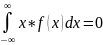 DX=
DX=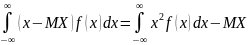 2
2
В
том случае, когда возможные значения
СВ Х ограничиваются конечным интервалом
(a,b)
пределами интегрирования в формулах
для математического ожидания и дисперсии
служат границы этого интервала. Т.к.
f(x)
и x2*f(x)
– четные функции, а x*f(x)-
нечетная, то по свойству интегралов от
нечетной и от четной функций MX=
DX
=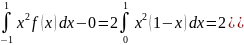 -1/4*
-1/4*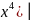
 =1/6
=1/6
2.6. Нормальное распределение.
СВ
Х называется нормально распределенной
СВ с параметрами m
и
2
, если ее плотность распределения равна
f(x)=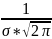 *
*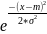
Непосредственным вычислением проверяется, что в этом случае
MX=m,
DX=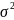 ,
т.е. параметры m
и
равны математическому ожиданию и
дисперсии СВ Х. Если СВ Х имеет нормальное
распределение с параметрами m
и
, то СВ
,
т.е. параметры m
и
равны математическому ожиданию и
дисперсии СВ Х. Если СВ Х имеет нормальное
распределение с параметрами m
и
, то СВ
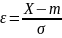 - нормальное распределение с
параметрами(0.1), поэтому ф.р. СВ Х Fx(x)
выражается через ф.р.
- нормальное распределение с
параметрами(0.1), поэтому ф.р. СВ Х Fx(x)
выражается через ф.р.
 (x)
случайной величины
(x)
случайной величины
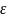 по формуле:
по формуле:
Fx(x)=P(X<x)=P(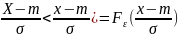
Аналогично
находим вероятность попадания СВ Х в
интервал (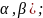
P(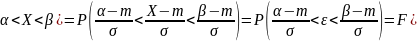 (2.16.)
(2.16.)
Ф.р.
F(x)=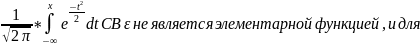 ее вычисления используют специальные
таблицы. В учебниках обычно приводится
таблица функции Ф(х)=
ее вычисления используют специальные
таблицы. В учебниках обычно приводится
таблица функции Ф(х)=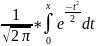 ,
связанной с F(x)
формулой :
,
связанной с F(x)
формулой :
F(x)=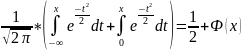
Функция
Ф(х) нечетная, Ф(-х)=-Ф(х), поэтому в таблице
приведены ее значения только для x≥0.
Заменяя в формуле (2.16) функцию F(x)
на ½+Ф(х) , получим для вероятности
попадания в интервал (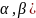 СВ Х, распределенной по нормальному
закону с параметрами m,
:
P(
СВ Х, распределенной по нормальному
закону с параметрами m,
:
P(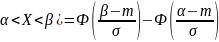 (2.17)
(2.17)
Пример1.7.
Считаетсячто отклонение длины
изготавливаемых деталей от стандарта
является случайной величиной,
распределенной по нормальному закону.
Найти , какой процент изделий имеет
длину от 49 до 51 см., если среднеквадратическое
отклонение длин от номинала равно
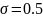 .
.
Решение.
Положив в формуле (2.17) m=50,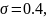
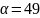 ,
,
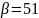 находим :
находим :
P(49<X<51)=Ф(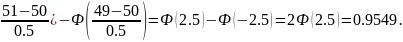
Т.е. ( в соответствии с законом больших чисел) 95% всех деталей имеет длину в пределах от 49 до 51 см.
