Министерство науки и образовАния Российской федерации Вятский государственный университет Факультет автоматики и вычислительной техники

КАФЕДРА ЭЛЕКТРОННЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИН

ОТЧЕТ

по циклу лабораторных работ

по дисциплине:

«Программирование на языках высокого уровня»

Выполнил: студент группы ВМ-12______________________/Курбатов А.А./

Проверил: доцент кафедры ЭВМ_______________________/Шиндяева Е.Н./

Киров 2010

Содержание

1. Лабораторная работа №1

   1. Задание и исходные данные…………………………………………………….3

   2. Тексты модулей………………….……….………………………………………5

   3. Схема передачи данных и управления…..………………………..……………8

   4. Экранные формы…………………………………………………………………9

2. Лабораторная работа №2

   1. Задание и исходные данные…………………………………………………...10

   2. Тексты модулей………………….……….……………………………………..11

   3. Схема передачи данных и управления…..………………………..…………..20

   4. Экранные формы……………………………………………………………..…21

3. Фоновая задача

   1. Постановка задачи. Цель……………………………………………………….25

   2. Тексты модулей…………………………………………………………………28

   3. Экранные формы………………………………………………………………..51

Лабораторная работа №1.

Конструирование и использование личной библиотеки.

Процедурные типы данных. Исследование методов численного интегрирования на программном уровне

Задание: Составить программу для вычисления интеграла методами: трапеций, Симпсона, прямоугольников.

Исходные данные:

Подынтегральная функция: у=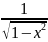

Пределы интегрирования [-0,5; 0,5]

Шаг интегрирования h=0.01

Контрольный результат: 1.04721

Теоретическая часть:

1. Метод трапеций.

Для вычисления интеграла 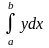разделяют промежуток интегрирования [a,b] на n равных частей [x₀,x₁], [x₁,x₂],..., [x_n-1,x_n] и к каждому из них применяют формулу трапеций 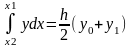, где h=(b-a)/n и обозначая через y_j=f(x_j)(j=0,1,...,n) значения подынтегральной функции в точках x_j. Окончательная формула:

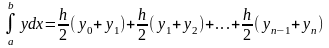
Или .

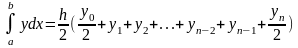2. Метод Симпсона

Пусть n=2m есть четное число и у_j=f(x_j)(i=0, 1, 2, ..., n) – значения функции у=f(x) для равноотстоящих точек a=x₀, x₁, ..., x_n=b с шагом .

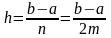Применяя формулу Симпсона 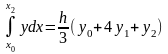, к каждому удвоенному промежутку [x₀,x₂], [x₂,x₄], ..., [x_2m-2,x_2m] длинны 2h окончательная формула будет иметь вид:

.

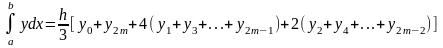3. Метод Трапеций

Пусть требуется определить значение интеграла функции на отрезке [a;b]. Этот отрезок делится точками на n равных отрезков Далее составляем суммы Каждая из сумм — интегральная сумма для f(x) на отрезке [a;b] и поэтому приближённо выражает интеграл:

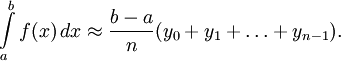
Очевидно, стоит рассчитывать на бо́льшую точность если брать в качестве опорной точки для нахождения высоты точку посередине промежутка. В результате получаем формулу средних прямоугольников:

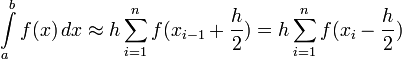
где

Текст основного модуля Integpro.pas:

Program Integraly;

Uses crt, integ;

Var xn,xk,h,S:real;

key,k:integer;

{$f+}

function f(x:real):real;

begin

f:=sqrt(1/(1-sqr(x)));

{ f:=sqrt(1-0.25*sqr(sin(x)));}

end;

{$f-}

BEGIN

clrscr;

Repeat

ClrScr;

textcolor(10);

begin

Vvod(xn,xk,h,p);

end;

textcolor (white);

writeln(' 1:Ввод исходных данных');

writeln(' 2:Метод прямоугольников');

writeln(' 3:Метод Симпсона');

writeln(' 4:Метод трапеций');

writeln(' 5:Сравнение методов');

writeln(' 6:Выход');

write(' Выберите нужный пункт меню: ');

readln(key);

textcolor(2);

Case key of

1: begin

writeln (' Введите исходные данные: ');

readln (xn,xk,h,p);

end;

2: begin

MetPryam(f,xn,xk,h,S,k);

end;

3: begin

MetSimpson(f,xn,xk,h,S,k);

end;

4: begin

MetTrapec(f,xn,xk,h,s,k);

end;

5: begin

textcolor (yellow);

MetPryam(f,xn,xk,h,S,k);

vivod (s,k);

MetSimpson(f,xn,xk,h,S,k);

vivod (s,k);

MetTrapec(f,xn,xk,h,s,k);

vivod (s,k);

readkey;

end;

readkey;

end;}

end;

if (key>1) and (key<5) then

begin vivod (s,k); readkey; end

until key=6;

end.

Текст модуля Integ.pas

Unit integ;

Interface

uses crt;

Type func=function (x:real):real;

var p:real;

Procedure Vvod(xn,xk,h,p:real);

Procedure MetPryam(f:func;a,b,h:real; var S:real; var k:integer);

Procedure MetSimpson(f:func;a,b,h:real; var S:real; var k:integer);

Procedure MetTrapec(f:func;a,b,h:real; var S:real; var k:integer);

Procedure Vivod(S:real;k:integer);

Procedure Pogresh(s:real);

Implementation

Procedure Vvod;

begin

writeln(‘ Подинтегральная функция y=(1-x^2)^(-1/2)');

writeln('Исходные данные: ',xn:2:1,' ',xk:5:3,' ',h:4:3,' ',p:6:5);

end;

Procedure MetPryam;

var x:real;

begin

writeln (Метод прямоугольников:');

S:=0;

x:=a+h/2;

k:=0;

Repeat

S:=S+f(x);

x:=x+h;

k:=k+1;

until x>b;

S:=S*h;

end;

Procedure MetSimpson;

var x:real;

i:integer;

begin

writeln (Метод Симпсона :');

S:=f(a)+f(b);

i:=1;

k:=0;

x:=a+h;

Repeat

If odd(i) then S:=S+4*f(x) else S:=S+2*f(x);

x:=x+h;

i:=i+1;

k:=k+1;

until x>=b;

S:=S*h/3;

end;

Procedure MetTrapec;

var x:real;

begin

writeln(Метод трапеций:');

S:=0;

x:=a+h;

k:=0;

Repeat

S:=S+f(x);

x:=x+h;

k:=k+1;

Until x>b;

S:=h/2*((f(a)+f(b))+2*S);

end;

Procedure Pogresh;

begin

writeln (' Абсолютная погрешность: ',abs(abs(s)-abs(p)):8:7);

writeln (' Относительная погрешность: ',(abs(abs(s)-abs(p))/abs(p)*100):8:6,'%');

end;

Procedure Vivod;

begin

textcolor(white);

writeln (' Полученный результат:',s:8:5);

Pogresh(s);

Writeln (' Количество итераций: ',k);

textcolor(yellow);

end;

End.

С хема передачи данных и управления

Экранные формы:

Г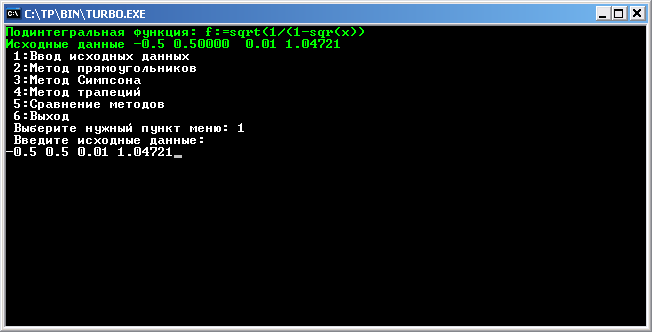 лавное меню и ввод исходных данных

О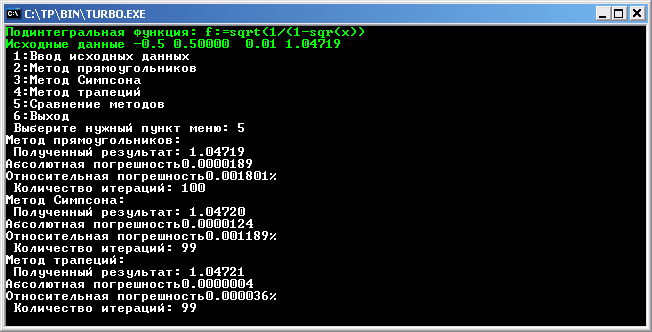 кно вывода результатов решения всеми методами: