
Задача № 3.
Приводятся фактические данные за 2003 год о распределении 74 территорий РФ по уровню среднедушевых ежемесячных расходов населения, тыс. руб.
Группы территорий РФ по уровню среднемесячных душевых расходов, тыс. руб., Mi |
Число территорий в каждой группе, fi |
до 1,98 |
6 |
от 1,98 до 3,44 |
33 |
от 3,44 до 4,90 |
25 |
от 4,90 и более |
10 |
Итого |
74 |
Задание:
Рассчитайте среднее значение признака, моду и медиану.
Рассчитайте абсолютные, средние и относительные показатели вариации.
Рассчитайте коэффициенты асимметрии и эксцесса.
Постройте на гистограмму распределения частот;
Выполните анализ полученных результатов, выводы оформите в аналитической записке.
Решение:
Выполним
расчёт серединного значения признака
в каждом интервале как полусуммы его
максимального и минимального значений:![]() .
Результаты представим в таблице:
.
Результаты представим в таблице:
Группы территорий РФ по уровню среднемесячных душевых расходов, тыс. руб., Мi |
Середина интервала |
Число территорий в каждой группе, fi |
до 1,98 |
0,99 |
6 |
от 1,98 до 3,44 |
2,71 |
33 |
от 3,44 до 4,90 |
4,17 |
25 |
от 4,90 и более |
5,63 |
10 |
Итого: |
|
74 |
Определим показатели вариации:
среднее значение признака -
 .
.
![]()
![]() тыс.руб.
тыс.руб.
среднее квадратическое отклонение -

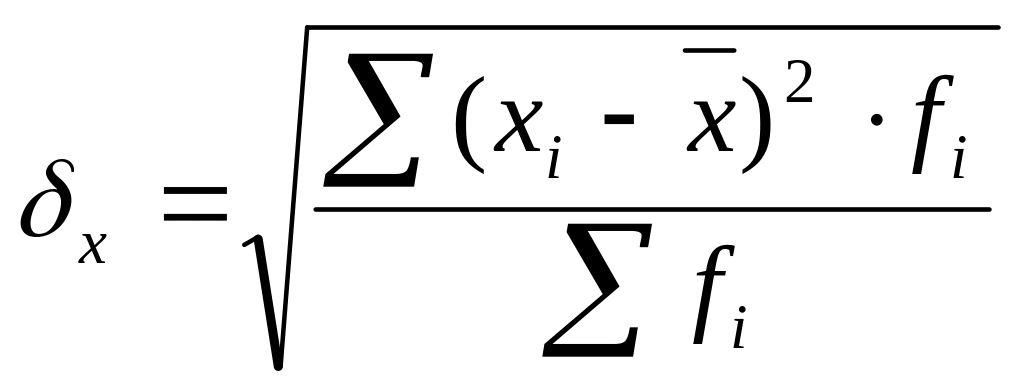
![]() тыс.руб.
тыс.руб.
3.
коэффициент вариации -![]()
![]()
4.коэффициент
асимметрии -![]() ,
где
,
где
![]() -
центральный момент третьего порядка;
-
центральный момент третьего порядка;
![]()
![]()
![]()
5.
значение моды -![]()
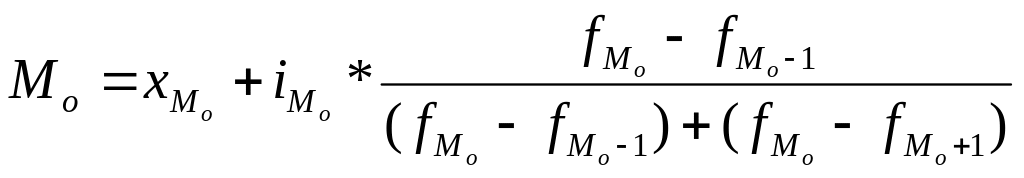 ,
где fм
– частота модального интервала; Хм –
нижнее значение модального интервала.
,
где fм
– частота модального интервала; Хм –
нижнее значение модального интервала.
Модальный интервал – интервал, где наибольшая частота.
![]() тыс.руб.
тыс.руб.
6.значение
медианы -
![]()
 ,
где fм
– частота медианного интервала; Хм –
нижнее значение медианного интервала.
,
где fм
– частота медианного интервала; Хм –
нижнее значение медианного интервала.
Медианный интервал – интервал, находящийся в середине ряда.
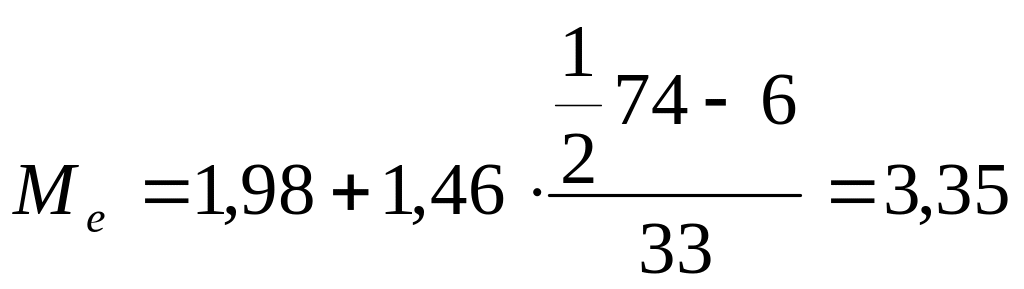 тыс.руб.
тыс.руб.
Построим гистограмму и полигон.
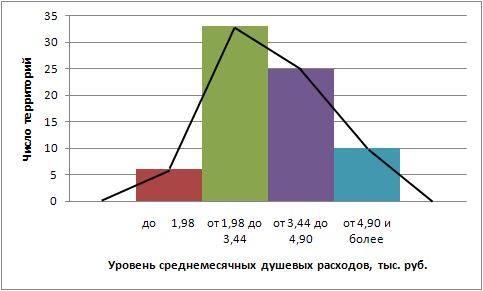
Из вышеприведенных вычислений можно сделать вывод:
наибольшее число территорий имеют уровень среднемесячных доходов в размере 3,11 тыс.руб., средний уровень среднемесячных доходов по всем территориям составляет 3,46 тыс.руб., значение коэффициента вариации в 36,02% означает неоднородность изучаемого признака, и большие отклонений от средней по всем территориям. Изучаемый ряд симметричен, о чем свидетельствует коэффициент асимметрии.
Задача №4.
Проанализируйте особенности структур, используя оценочные показатели различий структуры.
Приводятся данные за 2002 год по Северо-Западному федеральному округу.
Задание:
- рассчитайте показатели структуры; - рассчитайте оценочные показатели различий двух структур; - поясните, в чём причины различий структур.
Постройте график, иллюстрирующий различие двух структур.
Выводы оформите краткой аналитической запиской.
Территории |
Численность мигрирующего населения в 2002 году |
|||
Прибывших |
Выбывших |
|||
Всего, тыс. чел. |
В % к итогу |
Всего, тыс. чел. |
В % к итогу |
|
1. Респ. Карелия |
16,8 |
… |
14,9 |
… |
2. Респ. Коми |
16,8 |
… |
23,4 |
… |
3. Архангельская обл. |
16,5 |
… |
21,3 |
… |
4. Вологодская обл. |
14,6 |
… |
14,3 |
… |
5. Калининградская обл. |
20,7 |
… |
15,5 |
… |
6. Ленинградская обл. |
36,3 |
… |
23,0 |
… |
7. Мурманская обл. |
16,5 |
… |
24,7 |
… |
8. Новгородская обл. |
11,5 |
… |
10,4 |
… |
9. Псковская обл. |
13,9 |
… |
13,2 |
… |
10.г. Санкт-Петербург |
46,4 |
… |
38,4 |
… |
Итого |
210,0 |
100,0 |
199,1 |
100,0 |
Решение:
Выполним расчет долей как отношение частей к итогу, результаты сведем в таблицу.
Территории |
Прибывших |
Выбывших |
||
Всего, тыс. чел. |
В
% к итогу ( |
Всего, тыс. чел. |
В
% к итогу ( |
|
1.Респ. Карелия |
16,8 |
8,0 |
14,9 |
7,5 |
2. Респ. Коми |
16,8 |
8,0 |
23,4 |
11,8 |
3. Архангельская обл. |
16,5 |
7,9 |
21,3 |
10,7 |
4.Волгоградская обл. |
14,6 |
7,0 |
14,3 |
7,2 |
5.Калининградская обл. |
20,7 |
9,9 |
15,5 |
7,8 |
6.Ленинградская обл. |
36,3 |
17,3 |
23,0 |
11,6 |
7.Мурманская обл. |
16,5 |
7,9 |
24,7 |
12,4 |
8.Новгородская обл. |
11,5 |
5,5 |
10,4 |
5,2 |
9.Псковская обл. |
13,9 |
6,6 |
13,2 |
6,6 |
10.г. Санкт-Петербург |
46,4 |
22,1 |
38,4 |
19,3 |
Итого |
210,0 |
100 |
199,1 |
100 |
Выполним
расчёт абсолютных и нормированных
показателей различий 2-х структур.
Средние арифметические показатели
![]() ,
,
![]() определяются по следующим формулам:
определяются по следующим формулам:
![]() ;
;
![]() .
Здесь
.
Здесь
![]() и
и
![]() - показатели удельного веса, оценивающие
две структуры и выраженные в процентах:
- показатели удельного веса, оценивающие
две структуры и выраженные в процентах:
![]() .
Показатель
определяет на сколько процентов в
среднем отличается удельный вес каждой
группы двух структур, а оценка
показывает сколько процентных пунктов
составляют фактические различия двух
структур от величины их предельных
различий, составляющих 200%.
.
Показатель
определяет на сколько процентов в
среднем отличается удельный вес каждой
группы двух структур, а оценка
показывает сколько процентных пунктов
составляют фактические различия двух
структур от величины их предельных
различий, составляющих 200%.
Вспомогательный расчет произведем в таблице.
Территории |
Прибывших |
Выбывших |
|
2 |
|
|
||
Всего, тыс. чел. |
В % к итогу |
Всего, тыс. чел. |
В % к итогу |
|||||
1.Респ. Карелия |
16,8 |
8,0 |
14,9 |
7,5 |
0,5 |
0,3 |
56,0 |
64,0 |
2. Респ. Коми |
16,8 |
8,0 |
23,4 |
11,8 |
3,8 |
14,1 |
138,1 |
64,0 |
3. Архангельская обл. |
16,5 |
7,9 |
21,3 |
10,7 |
2,8 |
8,1 |
114,5 |
61,7 |
4.Волгоградская обл. |
14,6 |
7,0 |
14,3 |
7,2 |
0,2 |
0,1 |
51,6 |
48,3 |
5.Калининградская обл. |
20,7 |
9,9 |
15,5 |
7,8 |
2,1 |
4,3 |
60,6 |
97,2 |
6.Ленинградская обл. |
36,3 |
17,3 |
23 |
11,6 |
5,7 |
32,9 |
133,4 |
298,8 |
7.Мурманская обл. |
16,5 |
7,9 |
24,7 |
12,4 |
4,5 |
20,7 |
153,9 |
61,7 |
8.Новгородская обл. |
11,5 |
5,5 |
10,4 |
5,2 |
0,3 |
0,1 |
27,3 |
30,0 |
9.Псковская обл. |
13,9 |
6,6 |
13,2 |
6,6 |
0,0 |
0,0 |
44,0 |
43,8 |
10.г. Санкт-Петербург |
46,4 |
22,1 |
38,4 |
19,3 |
2,8 |
7,9 |
372,0 |
488,2 |
Итого |
210 |
100 |
199,1 |
100 |
22,8 |
88,3 |
1151,4 |
1257,8 |
![]() ;
;
![]()
Средние квадратичные показатели различий 2-х структур характеризуются особым порядком расчёта: здесь используется форма средней квадратичной:
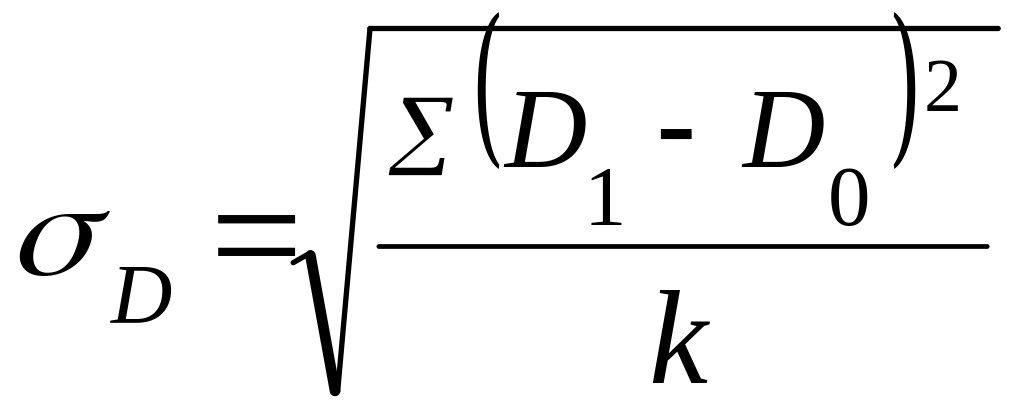 ;
;
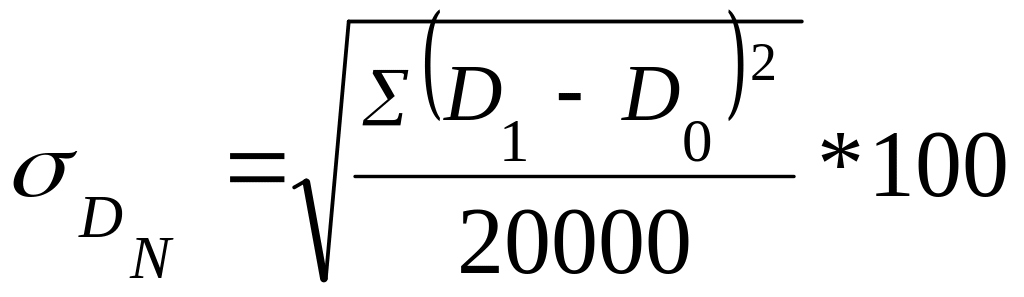 (процентных пунктов).
(процентных пунктов).
![]() ;
;
![]() %.
%.
Коэффициент
Гатева принадлежит к группе квадратичных
нормированных характеристик и показывает
сколько процентных пунктов составляют
фактические различия 2-х структур от их
возможных различий:
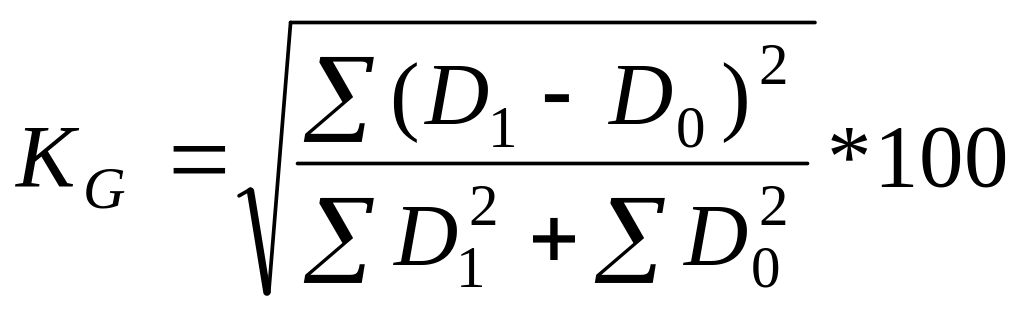 (процентных пунктов).
(процентных пунктов).
![]()
Таким образом, при расчете средних арифметических показатели , получили что: на 2,28% в среднем отличается удельный вес каждой группы двух структур и 11,4% процентных пунктов составляют фактические различия двух структур от величины их предельных различий, составляющих 200%.
При расчете средних квадратических показателей получили, что: на 2,97% в среднем отличается удельный вес каждой группы двух структур и 6,64% процентных пунктов составляют фактические различия двух структур от величины их предельных различий, составляющих 200%.
При расчете коэффициента Гатева получили, что фактические различия 2-х структур от их возможных различий составляют 19,14% процентных пунктов.
