Замкнутые множества, точки прикосновения, граница

Рассмотрим на плоскости какой-нибудь круг (рис. 2.5), причем берем и внутренние точки круга, и точки ограничивающей его окружности. Совершенно очевидно, что точка, находящаяся на окружности, не будет внутренней, так как не существует окрестности этой точки, которая бы целиком содержалась в круге, но также очевидно и то, что любая окрестность такой точки пересекается с множеством точек круга, более того, в любой окрестности точки, лежащей на окружности, содержится по крайней мере одна внутренняяточка круга.

Рис. 2.5

Эти простые соображения мотивируют следующее определение:

Определение 2.3. Точканазываетсяточкой прикосновения(илипредельной точкой) множества, если любая ее окрестность пересекается с, т.е..

Множество называется замкнутым, если оно содержит все свои точки прикосновения.

Подчеркнем, что точка прикосновения множества может и не принадлежать самому этому множеству.Например, если в качестве множествамы возьмем множество всех внутренних точек круга (рис. 2.5), то ни одна точка окружности, будучи точкой прикосновения, не принадлежит.

С другой стороны, понятно, что всякая внутренняя точка множества является точкой прикосновения этого множества.

Определение 2.4. Точка прикосновения множества, которая не есть его внутренняя точка, называетсяграничной точкоймножества.

Множество всех граничных точек множества называется егограницейи обозначается.

Объединение множества с его границей называется замыканием данного множества.

Замыкание договоримся обозначать(иногда используют обозначение, или).

Из определений сразу следует, что множество замкнуто тогда и только тогда, когда оно совпадает со своим замыканием.

Нетрудно видеть, что множествои, следовательно, замкнуто. Оно называется замкнутым шаром радиуса с центром в точке.

На прямой замкнутый шар - это отрезок; на плоскости - этокругвместе с ограничивающей его окружностью; в пространстве - шар вместе с ограничивающей его сферой.

Из определений сразу следует

Утверждение 2.4. 1) Для любого(замыкание замыкания совпадает с самим замыканием).

2. Для любых множеств изследует.

Взаимосвязь открытых и замкнутых множеств устанавливает простой, но фундаментальный результат:

Теорема 2.1. Множество открыто тогда и только тогда, когда его дополнение замкнуто.

Доказательство. Пусть множествооткрыто. Нам нужно доказать, что его дополнение, множество, замкнуто. Для этого достаточно доказать, что множествосодержит все свои граничные точки. Пусть. Если предположить, что, то это означает, что. Так как множествооткрыто, то любая его точка является внутренней. Следовательно найдется такое, что, т.е., что невозможно, так каклюбаяокрестность точки, как граничной точки множества, пересекается с. Значит,.

Обратно, пусть множество таково, что его дополнение замкнуто. Докажем, чтооткрыто. Предположим, что нашлась точка, не являющаяся внутренней. Это значит, что для любогопересечениене пусто. Но тогда точка- точка прикосновения множества,не принадлежащая ему, что невозможно ввиду замкнутости этого множества. Следовательно, любая точка множествавнутренняя, и это множество открыто.

Из теоремы 2.1 следует, в частности, что любое одноточечное множество в замкнуто.

Действительно, для любой точки найдутся окрестности, пересечение которых пусто: всегда можно выбрать(см. рис. 2.6). Заметим, что здесь существенно используются свойства расстояния, а именно, что прирасстояниеположительно. Отсюда, любая точкаимеет окрестность, не содержащую фиксированную точку, т.е. множествооткрыто, и само одноточечное множествозамкнуто.

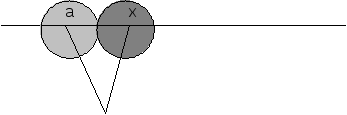Рис. 2.6.

Таким образом, замкнутость одноточечных множеств в следует из того фундаментального факта, чтолюбые две несовпадающие точки этого пространстваимеют непересекающиеся окрестности. Это свойство называют свойствомхаусдорфовости пространства (в честь выдающего немецкого математика Ф. Хаусдорфа).

Поскольку замкнутые множества - это в точности дополнения открытых, легко по аналогии с утверждением 2.2 доказать

Утверждение 2.5. Объединение любого конечного и пересечение любого семейства замкнутых множеств замкнуто.

Тот факт, что объединение бесконечного семейства замкнутых множеств может оказаться и не замкнутым, вытекает из такого примера. Рассмотрим семейство замкнутых шаровс центром в какой-то точкедля всех, строго меньших некоторого фиксированного. Нетрудно догадаться, что объединением этого семейства будетоткрытыйшар.

Все пространство , с одно стороны, как дополнение пустого множества, замкнуто, но оно же, как мы видели ранее, также и открыто. Значит, пустое множество и все пространство суть множества, которыеоткрыты и замкнуты одновременно. Этотривиальныепримерыоткрыто-замкнутых множеств(т.е. множеств, открытых и замкнутых одновременно). В самом пространстве, однако, нельзя построить нетривиальный пример открыто-замкнутого множества.

Легко построить примеры множеств, которые ни открыты, ни замкнуты. Простейшим примером в одномерном случае может служить полуинтервал(или). Это множество не открыто потому, что один из его концов не является внутренней точкой, тогда как другой будет граничной точкой, не принадлежащей самому множеству. Чуть более замысловатым примером множества, не являющегося ни открытым, ни замкнутым, является следующее: берем на плоскости множество всех внутренних точек какого-нибудь круга и добавляем к нему любоесобственноеподмножество точек ограничивающей круг окружности. Зеркально: можно взять все точки окружности и добавить множество внутренних точек круга, выбросив из него любое конечное подмножество («замкнутый круг с дырками»). Но если мы возьмемвнутрикруга произвольноеконечноемножество точек, а затем добавим к нему границу круга, т.е. окружность, получим замкнутое множество (почему?). Подумайте, какое множество получится, если рассмотреть внутренность круга и выбросить из нее произвольное конечное множество точек («открытый круг с дырками»).