10

Глава 2. Дифференциальное исчисление функций нескольких вещественных переменных

Предмет исследования в данной главе - функции вида

, (1)

т.е. функции, определенные на некотором подмножествеевклидова пространстваи принимающие значения в евклидовом пространстве. Как правило, мы полагаем, что, тогда как. Тем самым рассматриваются функции «векторного аргумента», принимающие скалярные (при) или векторные (при) значения. Для таких функций мы должны обобщить известные из курса математического анализа первого семестрапонятия непрерывности, дифференцируемости(изученные для случая), а потом на этой основе дать аппаратисследованиятаких функцийна экстремум. В построении теории мы существенным образом используем методы линейной алгебры (глава 1).

Если задана функция вида (1), то тем самым каждому -мерному вектору, принадлежащему области определения функции, сопоставлен однозначно- мерный вектор, обозначаемый тогда как:

(2)

Вводя в пространствах икакие-то базисы (будем далее молчаливо предполагать, что рассматриваются только ортонормированные базисы; более того, как правило, мы считаем, что «работаем» в канонических базисах арифметических векторных пространств), мы можем переписать равенство (2) в координатной форме:

(3)

где - столбцы координат векторовисоответственно в выбранных базисах.

Функции в равенствах (3) называютсякоординатными функциямифункции (1). Каждая координатная функция есть числовая (скалярнозначная) функция, зависящая отвещественных переменных (или, что то же самое, от одной-мерной векторной переменной), определяющая значения той или иной координаты вектора, являющегося значением функции (1).

Векторная функция вида (1) может быть задана непосредственно своими координатными функциями.

Например:

Записанная таким образом функция есть функция, отображающая двумерные векторы в двумерные. Областью ее определения (как и областью значения) служит все пространство . Вводя ограниченияи переходя к более традиционным обозначениям переменных, получим функцию

определенную в «полуполосе» (см. рис. 2.1) и задающую переход от полярных координат на плоскости к обычным декартовым координатам.

Рис. 2.1

Следующая функция является числовой и потому совпадает со своей единственной координатной функцией:

Понятно, что областью определения этой функции служит множество внутренних точек круга единичного радиуса с центром в начале координат.

Обратим внимание на то, что пространство со стандартно определенным скалярным произведением векторов (см. гл. 1, п. 1.18) рассматривается какметрическое пространство, т.е. пространство, для любых двух точек (векторов)которого определено расстояние между ними как

,

обладающее следующими свойствами (см. п. 1.5):

1. , причемтогда и только тогда, когда;

2. ;

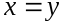3. (неравенство треугольника).

   В заключение этой «преамбулы» заметим, что в первой главе мы занимались преимущественно функциями вида (1), которые были определены на всем пространстве и были линейны, т.е. мы изучалилинейные отображениямежду евклидовыми пространствами(хотя, рассматривая билинейные и квадратичные формы, мы уже выходили за рамки чистой линейности, переходя к так называемой «полилинейности»). Во второй главе мы займемся гораздо более широким классом нелинейных функций вида (1) и построим для них дифференциальное исчисление, обобщающее обычное дифференциальное исчисление функций одной вещественной переменной.