
- •Содержание
- •Введение
- •Глава 1 особенности структуры и технологии наноразмерных объектов
- •1.1 Классификация вещественных объектов
- •1.1.1 Размерные классы частиц
- •1.1.2 Факторы, влияющие на свойства вещества
- •Риcунок 1.11 – Схема возникновения н-центра окраски в цгк типа NaCl
- •1.2 Методы получения низкоразмерных частиц
- •1.3 Модельные представления о структуре и габитусе наноразмерных частиц
- •1.3.1 Методологические подходы к описанию кристаллов
- •1.3.2 Правильные формы кристаллов и их описание
- •Общие простые формы кристаллов и кристаллографические индексы их граней (hkl)
- •Частные простые формы (грань (h 0 0))
- •Частные простые формы кристаллов с единичным направлением (исходная грань (h k 0)).
- •Частные простые формы кристаллов без единичного направления
- •1.3.3 Габитус наночастиц, полученных при диспергировании крупных кристаллов
- •1.4 Теоретическое описание структуры и габитуса наночастиц, полученных конденсированием
- •1.4.1 Шаровые упаковки как модели многоатомных структур
- •1.4.2 Атомные координации в полиэдрах плотнейших атомных упаковок
- •Радиусы координационных сфер и их числа заполнения для гцк-структур
- •Радиусы координационных сфер и их числа заполнения для гпу-структур
- •Радиусы координационных сфер и их числа заполнения для оцк-структур
- •1.4.3 Некристаллографическая симметрия габитуса наноразмерных атомных координационных полиэдров
- •1.4.4 Фуллереноподобные формы нанокристаллов
- •1.4.5 Габитусы наночастиц сложного состава
- •1.5 Структура и свойства наноразмерных частиц, применяемых в функциональном материаловедении
- •1.5.1 Структура и свойства наноразмерных металлических модификаторов функциональных материалов
- •Координационные числа (к) координационных сфер (n – ее номер) при плотнейшей шаровой упаковке
- •Основные параметры, необходимые для описания жидких кластеров металлов (z – порядковый номер, n – плотность атомов, ef – энергия Ферми, rw – радиус Вагнера-Зейтца, w – работа выхода)
- •1.5.2 Наноразмерные углеродсодержащие модификаторы*
- •Размеры кристаллических блоков в алмазосодержащих продуктах детонационного синтеза
- •Р исунок 1.66 – Термограммы tg (а) и dta (б) углеродных нанокластеров. Скорость нагрева 5оС/мин: 1 – удаг; 2 – уда
- •Фазовый состав наномодификаторов, полученных по технологии термолиза прекурсора в технологической среде
- •Характеристики модифицированных углеродных волокон [161]
- •1.5.3 Силикатные наноразмерные частицы
- •Кристаллографические индексы рефлексов (kl) и структурные амплитуды f(20) и f(850) кристалла мусковита при 20оС и после прогрева при 850оС соответственно
- •Характеристики ультрадисперсных керамик (ук), полученных плазмохимическим синтезом [179]
- •Характеристики ультрадисперсных керамик (ук) механохимического синтеза [177]
- •Характеристики ультрадисперсных оксинитридов плазмохимического синтеза [179-180]
- •Некоторые свойства природных и синтетических цеолитов
- •1.6 Заключение к главе 1
- •Глава 2 механизмы модифицирующего действия наноразмерных частиц в полимерных и олигомерных матрицах
- •2.1 Критерии оценки наноразмерности
- •2.1.1 Физические предпосылки к оценке наноразмерности частиц
- •2.1.2 Связь фононных характеристик с наноразмерностью
- •2.1.3 Теорема Блоха и наноразмерность
- •2.1.4 Дебаевская длина волны и максимальный наноразмер
- •2.1.5 Расчет максимального наноразмера на основании уравнения Шредингера
- •2.1.6 Определение предельных размеров частиц веществ с неразрушенными полимерными молекулами
- •2.1.7 Динамические модели кристалла Эйнштейна и Дебая
- •2.1.8 Расчетные значения максимальных размеров наночастиц одноэлементных веществ и некоторых соединений
- •Характеристические температуры ( ) и максимальные размерынанокристаллов некоторых веществ
- •Характеристические температуры и максимальные размеры нанокристаллов некоторых галогенидов
- •Температура Дебая и максимальный наноразмер полупроводников типов
- •Отношение температуры Дебая наночастиц к для объемной фазы некоторых металлов, r – размер частицы
- •Дебаевская температура и наноразмерный максимум одноэлементных веществ
- •2.1.9 Влияние размеров кристаллитов на их физические свойства
- •2.2 Особенности зарядового состояния наноразмерных частиц
- •2.2.1 Зарядовое состояние дисперсных частиц слоистых минералов
- •2.3 Зарядовое состояние металлических компонентов функциональных материалов и металлополимерных систем
- •2.3.1 Модельные представления о механизме модифицирования полимерных матриц нанокомпозиционными частицами
- •Зависимость размеров областей когерентного рассеяния (l ǻ) от массовой концентрации (с, мас.%) ультрадисперсного углерода (шихты)
- •Значения радиусов (r, ǻ) и относительных координационных чисел (окч) для композитов с различной массовой концентрацией (с, мас.%) наполнителя
- •2.4 Заключение к главе 2
2.3.1 Модельные представления о механизме модифицирования полимерных матриц нанокомпозиционными частицами
Как ранее отмечалось, нанокомпозиционные машиностроительные материалы на основе полимерных матриц находят все большее применение при создании герметизирующих устройств, узлов трения машин, механизмов и технологического оборудования, функциональных покрытий. Марочный ассортимент низкоразмерных модификаторов непрерывно расширяется и включает металлические, силикатные, углеродные компоненты в виде простых веществ и соединений типа нитридов, карбидов, солей и др. [16-27, 65-67]. Это требует разработки методологии оптимального выбора модификаторов, обеспечивающих заданный уровень служебных характеристик композиционных материалов.
В настоящем разделе рассмотрены физические аспекты модифицирующего действия наноразмерных частиц наполнителя в модельных системах на основе полимеров.
В модельных композиционных системах, которые состоят из связующего и наполнителя, можно выделить три характерных типа веществ (рис. 2.39): вещество частицы (Ч), связующее (С) и прилегающая к частице часть связующего (граничный слой, П).

Рисунок 2.39 – Составные части модельного композита: частицы наполнителя (Ч), связующее (С), граничный слой (П)
Таким образом, экспериментальные данные, полученные из литературных источников и проведенных исследований, свидетельствуют о наличии характерного энергетического состояния поверхностных слоев компонентов трибосистемы, которое вносит существенный вклад в механизм ингибирующего действия функциональных наноматериалов.
Рассмотрим простейший случай, когда наночастицы и модифицированные ими области имеют сферические формы. Пусть объем системы равен , число наночастиц равно N, радиус частицы rj, толщина модифицированного приповерхностного поля hj.
Следовательно,
объем частицы равен
![]() ,
объем модифицированной области Wj:
,
объем модифицированной области Wj:
![]() . (2.155)
. (2.155)
Если N – число частиц, Vj – объем j-той частицы, то величина Сv
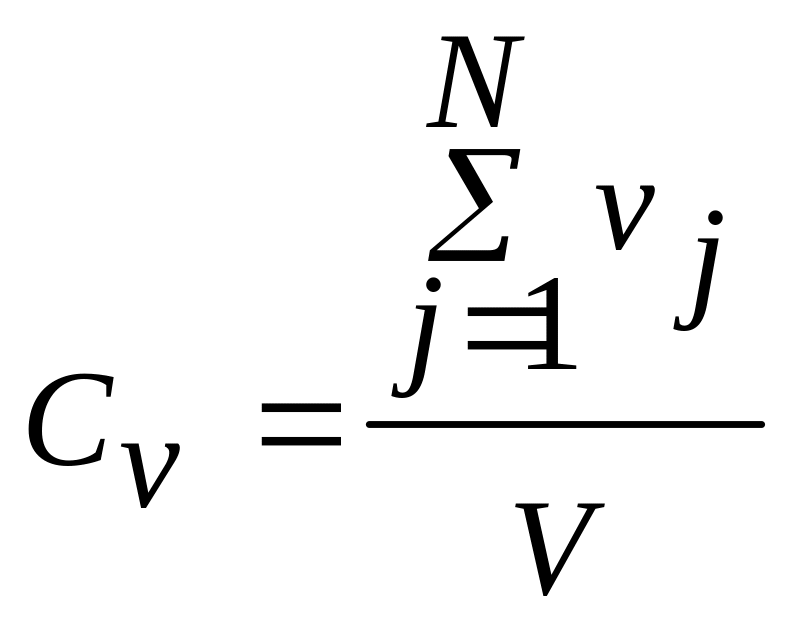 (2.156)
(2.156)
определяет относительный объем, занятый наночастицами, или коэффициент заполнения (коэффициент упаковки). Отношение
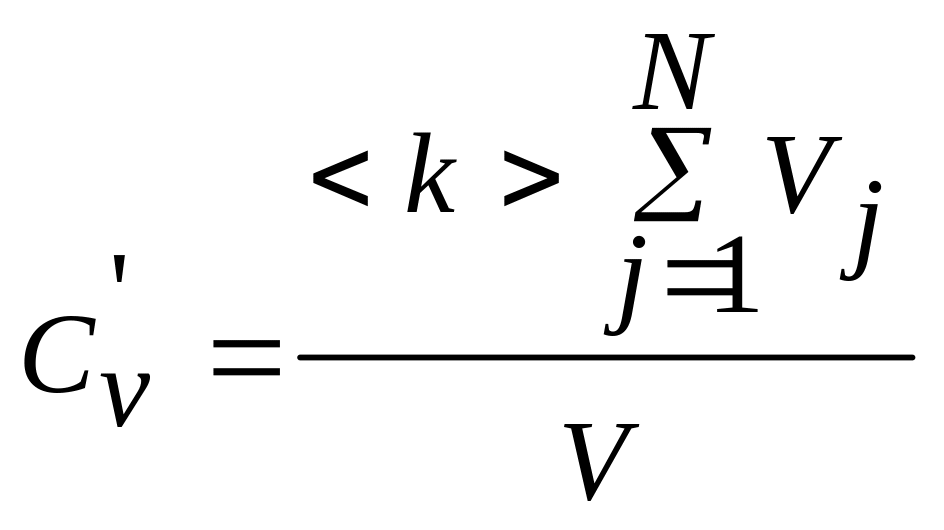 (2.157)
(2.157)
представляет собой относительный модифицированный объем, <k> коэффициент перекрытия участков, модифицированных частицей наполнителя.
Из экспериментов известно, что даже при небольшой концентрации наноразмерных частиц модификатора (до 0,1 мас.%) свойства композита на основе полимера могут существенно изменяться. В частности, для деталей изготовленных из модифицированных термопластов, износостойкость и прочностные характеристики могут увеличиваться на 20–30 % [16, 22, 23, 37]. Для объяснения этого экспериментально зафиксированного факта можно использовать следующую модель.
Пусть массовая концентрация частиц наполнителя Сm, масса и плотность наполнителя mf и f соответственно, mв, в – то же для связующего. Тогда:
![]() . (2.158)
. (2.158)
Отсюда, объемная концентрация наполнителя (2.156) равна:
![]() . (2.159)
. (2.159)
Если объем (и радиусы) частиц модификатора одинаков, то:
![]() .
(2.160)
.
(2.160)
Пусть толщина модифицированного слоя равна h, тогда для достижения полного модифицирования необходимо выполнение условия:
![]() . (2.161)
. (2.161)
где К – коэффициент, учитывающий перекрывание и компактность модифицирующих областей.
Из условий (2.160) и (2.161) следует:
![]() . (2.162)
. (2.162)
Так как mв>>mf, то условие (2.159) можно представить в виде:
![]() . (2.163)
. (2.163)
Тогда выражение (2.162) примет вид:
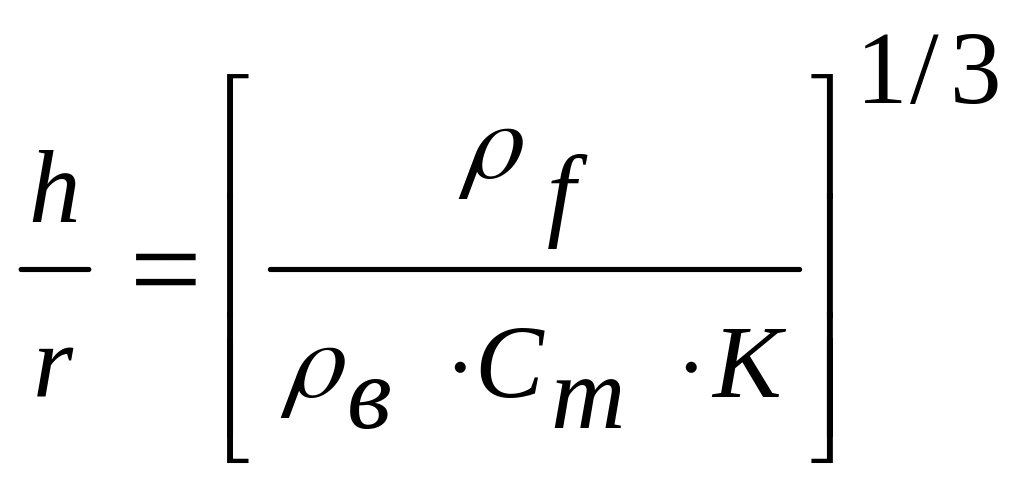 . (2.164)
. (2.164)
Для предельного случая, когда частицы располагаются в точках, соответствующих плотнейшей упаковке шаров с радиусом (r+h), и перекрывание отсутствует, К=0,74. При f/в=4 (достаточно типичный случай) и Св = 0,1 % получим:
h15r. (2.165)
Естественно, применение предложенной модели имеет ограничения, потому что, во-первых, надо доказать, что условие (2.165) выполнимо, а, во-вторых, необходимо учитывать, что при создании композита трудно достичь равномерного распределения модифицирующих частиц по объему связующего. Действительно, в работе [72] показано, что в соответствии с эргодической теоремой в каждой точке вещества композита при его перемешивании происходят флуктуационные изменения плотности, то есть возникают дивергентные потоки, что обуславливает возникновение и исчезновение кластерных структур. При этом возможно не только образование, но и разрушение кластеров (рис. 2.40).
Известно, что многие низкоразмерные частицы обладают собственным нескомпенсированным зарядом с большим временем релаксации [23, 37, 66]. Если модифицированный объем в композите рассматривать как молекулярный кластер, то его формирование вокруг заряженной частицы модификатора можно описать следующим образом. Вследствие того, что увеличение размеров кластеров происходит в результате взаимодействия поляризованных молекул среды, то из теоретического анализа процессов создания композита в рамках различных приближений всегда следует вывод, что процесс образования кластеров в композиционных полимерных системах неизбежен. Для моделирования этого явления возможно использование представлений, изложенных в [73, 74].

а б в
Рисунок 2.40 – Переход частицы от одного 10-ти частичного кластера к другому: а – исходное положение, б – движение частицы через потенциальный барьер, в – укрупнение и уменьшение кластеров
допинговых Рассмотренная модель с учетом 2.165 и [73-79], позволяет понять модифицирующее действие, то есть малых массовых концентраций наноразмерных частиц. Однако, для более строгого аргументирования адекватности этой модели реальным процессам необходимо обосновать возможность возникновения зарядов на поверхности нанокристаллических частиц [80-88].
Для экспериментальной проверки полученных модельных представлений о механизме реализации модифицирующего действия наноразмерных частиц в полимерных матрицах были получены композиты с допинговыми добавками ультрадисперсных частиц углерода детонационного синтеза (УДАГ).
В качестве объекта исследования был использован полиэтилен низкого давления (ПЭНД) марки 227-03 (ГОСТ 16338-85) и полиэтилен высокого давления (ПЭВД) марки 16207-029 (ГОСТ 16337-85). Полимеры модифицировали ультрадисперсными частицами углерода, полученными методом детонационного синтеза (шихта). Удельная поверхность частиц наполнителя составляла 30030 м2/г. Размеры единичных частиц наполнителя составляла 3-8 нм, а устойчивых агрегатов – 20-30 нм. Композиции готовили методом механического смешивания порошков исходных полиолефинов с наполнителем. Образцы для физико-механических испытаний получали методом литья под давлением [80].
Для определения структурных изменений модифицированных ПЭНД и ПЭВД анализировали рентгенограммы, полученные на рентгеновском дифрактометре ДРОН-2,0 при фильтрованном CuKа излучении.
Средний размер областей когерентного рассеяния (L) рассчитывали по формуле Шеррера:
![]() ,
,
где
длина рентгеновского
излучения (1,54 Ǻ),
![]() полуширина и угловое
положение максимума соответственно
[84].
полуширина и угловое
положение максимума соответственно
[84].
Для более детального рассмотрения
структурных изменений в ПЭ при введении
ультрадисперсных кластеров наполнителя
строились корреляционные функции W(r),
связанные с функциями радиального
распределения атомной плотности (ФРРАП)
![]() ,
методика построения которых описана в
работах [85-87].
,
методика построения которых описана в
работах [85-87].
На рентгенограммах ПЭНД и ПЭВД, модифицированных частицами шихты, в области углов дифракции 2=15о-25о наблюдается гало с наложенными на него достаточно выраженными максимумами в области углов 2=37о-46° имеется второе более размытое гало (рис. 2.41). Анализ рентгенограмм свидетельствует о том, что существенного изменения содержания кристаллической фазы в композитах не происходит.
В табл. 2.7 приведены экспериментальные значения размеров областей когерентного рассеяния (L Ǻ, см) в зависимости от массовой концентрации (С, мас.%) шихты. Видно, что, во-первых, изменения L для различных образцов в ряде случаев существенно превышают погрешности эксперимента, а, во-вторых, L не изменяются монотонно с ростом С, мас.%. Действительно, для ПЭНД
![]() %
%
При экспериментальной погрешности
![]() %.
В то же время
%.
В то же время
![]() ,
но
,
но
![]()
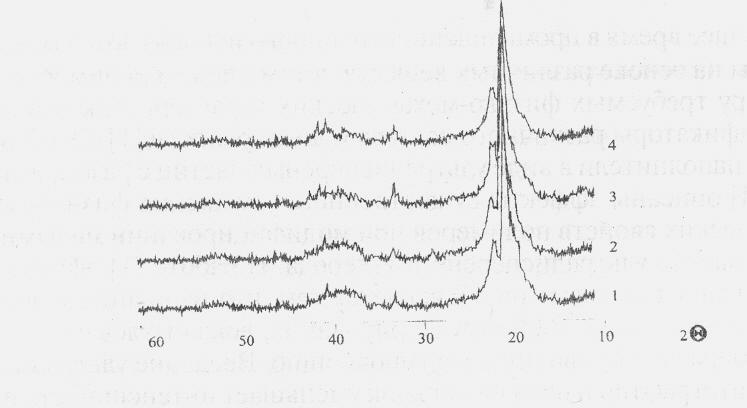
Рисунок 2.41 – Рентгенограммы полиэтиена высокого давления, модифицированного УДА с различной массовой концентрацией (С, мас.%): 1 – исходный, 2 – 0,01 мас.%, 3 – 0,01 мас.%, 4 – 1,0 мас.%
Таблица 2.7
