МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ВОЛЖСКИЙ ИНСТИТУТ СТРОИТЕЛЬСТВА И ТЕХНОЛОГИЙ (ФИЛИАЛ)

ГОУ ВПО «ВОЛГОГРАДСКОГО АРХИТЕКТУРНО-СТРОИТЕЛЬНОГО УНИВЕРСИТЕТА»

Кафедра «Высшей математики»

«Интеграл и его приложения»

Методические указания к изучению темы и индивидуальные задания

Волжский 2010г.

«Интеграл и его приложения». Методические указания к изучению темы и индивидуальные задания / ВИСТех (филиал) ВолгГАСУ; [сост. к.т.н. Д.П. Торшин, к.т.н. Е.Д. Илларионова]. – Волжский : ВИСТех (филиал) ВолгГАСУ, 2010. – 50 с.

В данной работе рассмотрена методика решения типовых примеров и задач по теме: «Интеграл и его приложения» и предложены индивидуальные задания с учетом специальных дисциплин технического вуза. Особое внимание уделено приложениям интеграла в соответствии с требованиями ГОСа обучения высшей математики на инженерных специальностях.

Для студентов 1 курса дневной формы обучения.

Введение

Методические указания позволяют овладеть приемами интегрирования функций, научиться применять интеграл к решению практических задач. Выполнение индивидуальных заданий потребует знания общих методов интегрирования: методов подставки (замены переменной), интегрирования по частям. В ряде случаев приведут к цели приемы непосредственного интегрирования, опирающиеся на основные свойства неопределенных интегралов, подведения под знак дифференциала (одна из форм замены переменной). Потребуется также знание специфических приемов интегрирования, зависящих от типа подынтегральной функции (рациональные функции, простейшие и квадратические иррациональности и т.д.)

В каждом конкретном примере может возникнуть необходимость сочетания общих методов и специфических приемов интегрирования.

I ЧАСТЬ

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. ОСНОВНЫЕ СВЕДЕНИЯ ПО ТЕМЕ.

Напомним таблицу простейших и часто встречающихся интегралов, основные свойства неопределенных интегралов и основные методы интегрирования.

1. ТАБЛИЦА ПРОСТЕЙШИХ И ЧАСТО ВСТРЕЧАЮЩИХСЯ ИНТЕГРАЛОВ

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

2. ОСНОВНЫЕ СВОЙСТВА НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ

2.1.

2.2.

2.3. Если , то

3. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ

3.1.Метод подстановки (метод замены переменной)

Метод подстановки часто применяют в виде равенства:

где - новая переменная интегрирования.

Например:

Метод подстановки, применяемый в таком виде, нередко называют методом подведения под знак дифференциала (ниже рассмотрим еще несколько примеров его применения).

В ряде случаев метод подставления, применяют в виде формулы:

получаемый в результате замены переменной

Например: При вычислении интеграла необходимо ввести новую переменную т.е. .

Тогда: .

3.2. Метод интегрирования по частям

Метод интегрирования по частям основан на использовании формулы: (1)

где - дифференцируемые функции.

Например: При вычислении интеграла , полагаем , .

Тогда имеем: .

Замечание: При использовании формулы (1) нужно подынтегральное выражение представить рационально в виде так, чтобы выражение было интегрируемое, а интеграл должен оказаться или берущимся, или, во всяком случае, не более сложным, чем исходный интеграл.

4. Методические указания к выполнению индивидуальных заданий

Каждый вариант индивидуальных заданий содержит (27) неопределенных интегралов.

В примерах №1-14 целесообразно использовать метод подстановки.

Необходимо, прежде всего, проанализировать структуру подынтегральной функции, подобрать замену, используя формулы из таблицы производных (дифференциалов) и выполнить преобразование подынтегрального выражения, приводящие к возможности использования соответствующих формул из таблицы интегралов.

Пример 1.

Сделав замену:   , получим:

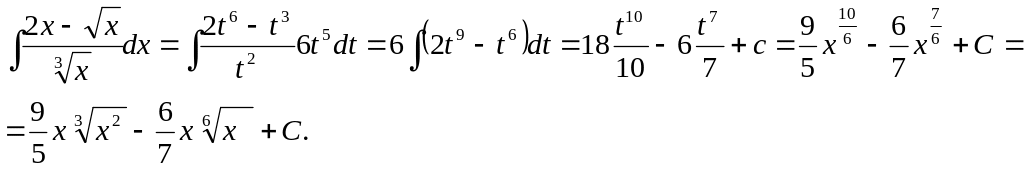
Пример 2.

Введем новую переменную по формуле .

Тогда т.е.

.

Пример 3.

Заметив, что можно записать:

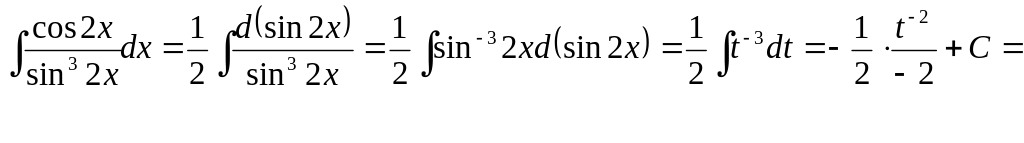
где

Пример 4.

Обозначив и, учитывая, что

Получим .

В примерах №22-24 интегралы берутся методом интегрирования по частям с помощью формулы (1).

При интегрировании выражений типа принимают за а за или при интегрировании выражений типа принимают за а за

Пример 5.

Чтобы воспользоваться формулой (1) считаем

, тогда

В некоторых случаях формулу (1) необходимо применять несколько раз.

Пример 6.

Введем ,  , , .

По формуле (1) .

Чтобы найти , применим еще раз интегрирование по частям. Полагаем и

В примерах №25-27 даны интегралы от тригонометрических функций. В зависимости от вида подынтегральной функции используют замену переменной (пр. 25, 26 и некоторые пр. 27), специального приёма – выделения множителя и замены , и или преобразование произведения в сумму при помощи следующих формул:

Пример 7.

Пример 8.

.

Пример 9.

Пример 10.

В примере №18 всех вариантов нужно выделить под корнем полный квадрат по формуле и найти интеграл по одной из табличных формул.

Пример 11.

В примерах №19-20 необходимо в числителе выделить слагаемое, равное производной трехчлена, стоящего в знаменателе. Затем данный интеграл представить в виде суммы двух интегралов, один из которых вычисляется по формуле , а второй по формуле (12 или 13) после выделения полного квадрата в знаменателе.

Пример 12.

Метод нахождения интеграла в примере №21 аналогичен рассмотренным выше, однако в результате используются другие интегралы, а именно:

и табличные (14) или (15).

Пример №13.

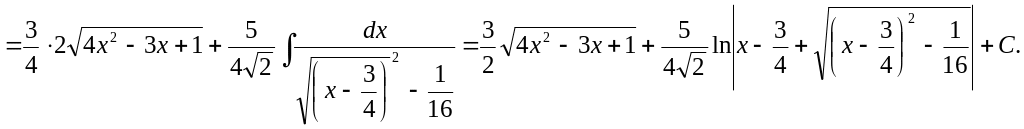При интегрировании дробно-рациональных функций (пример №16) прежде всего, необходимо выделить целую часть, если дается дробь неправильная, и соответствующую правильную дробь. Знаменатель правильной дроби разложить на простейшие множители типа

В соответствии с этим разложением заменить данную правильную дробь в виде суммы простейших дробей и проинтегрировать полученные простейшие дроби.

Пример 14.

Подынтегральная функция является неправильной дробью. Выделим целую часть неправильной рациональной дроби:

Итак,

Отсюда находим:

Запишем подынтегральную функцию в виде суммы простейших дробей с неопределенными коэффициентами:

Далее, справа приводит к общему знаменателю и, освобождаясь от знаменателей, получим:

Действительными корнями знаменателя являются числа -2, -1, 2.

При х=-2, имеем 71=4В, В= ;

При х=-1, имеем 9=-3А, А=-3;

При х=2, имеем -69=12С, С= .

Следовательно:

По этому: .