1.2.Расчет размерной цепи с использованием теории вероятностей.

Расчет выполняется с учетом заданного риска получения брака Q, значение которого определено заданием на расчет. При проектном расчете, если нет других соображений, принимаем нормальный закон распределения значений для всех звеньев.

Исходной предпосылкой теоретико – вероятностных методов расчета является совпадение границ рассеяния значений звеньев с границами полей допусков. Заданный риск получения брака говорит о том, что границы рассеяния значений замыкающего звена, получаемые при сборке, не совпадают с границами поля допуска и могут выходить за их пределы с вероятностью Q. Для учета этого обстоятельства в расчетные формулы вводят коэффициент риска t , равный отношению размаха к величине допуска замыкающего звена при заданном Q.

Расчет начинаем с проверки условия замкнутости по формуле (1). (Не смотря на то, что этот расчет был уже выполнен ранее, для корректности изложения его надо повторить).

Вычисляем коэффициент риска для нормального закона распределения значений замыкающего звена.

Определяем значение нормированной

функции Лапласа: Ф(z) = (1 – Q/100%)/2 .

Из таблицы 3 найдем значение аргумента нормированной функции Лапласа z , соответствующее полученному Ф(z).

Коэффициент риска будет равен

t = 3/z.

Таблица 3. Значения нормированной функции Лапласа.

z	Ф(z)	z	Ф(z)	z	Ф(z)
1,85 1,90 1,95 2,00 2,05 2,10 2,15 2,20	0,4678 0,4713 0,4744 0,4773 0,4798 0,4821 0,4842 0,4861	2,25 2,30 2,35 2,40 2,45 2,50 2,55 2,60	0,4878 0,4893 0,4906 0,4918 0,4929 0,4938 0,4847 0,4953	2,65 2,70 2,75 2,80 2,85 2,90 2,95 3,00	0,4960 0,4965 0,4970 0,4974 0,4978 0,4981 0,4984 0,49865

Реализуя метод равных допусков, вычисляем расчетное значение допуска

.

Смысл и значения величин, входящих в формулу, такой же, как в формуле (2).

Используя таблицу 1, назначаем стандартные допуски звеньев, ближайшие к расчетному з начению.

Проверяем выполнение условия

Если условие не выполняется, то для одного – двух звеньев назначаем допуски по более точному квалитету.

Дальнейшая последовательность расчета изложена в учебном пособии [1] (раздел 2.3.4).

2.Расчет посадки с натягом

Расчет посадки с натягом выполняем для бесшпоночного соединения зубчатого колеса с валом (рис. 3). Изложение раздела должно соответствовать примеру из книги [1] с учетом требований раздела 4.

1 – вал, 2 – зубчатое колесо

Рисунок 3 - Соединение с натягом

Исходными данными для расчета являются параметры соединения (рис.3) , механические характеристики материалов вала и зубчатого колеса, передаваемая нагрузка.

Параметры соединения определяем на основании исходных данных.

Диаметр делительной окружности, мм

d = m · z / cos β ,

где m – модуль зацепления, z – число зубьев колеса., β – угол наклона зубьев (значения m, z и β определены заданием).

Диаметр сопряжения - диаметр вала под зубчатым колесом, мм

D = d _к = d _п + 5…7 .

Здесь d _п – диаметр вала под подшипник.

Полученное значение диаметра следует округлить до ближайшего значения из ряда нормальных линейных размеров (ГОСТ 6636): 28, 30, 32, 34, 36, 38, 40, 42, 45, 48, 50, 53, 56, 60, 63, 67, 71, 75, 80, 85, 90, 95, 100, 105, 110, 120, 125, 130, 140, 150, 160, 170 … .

Длину ступицы принимаем в интервале значений

l _ст = (0,8 … 1,2) d _к

(любое значение в указанном интервале), согласуя его с рядом нормальных линейных размеров.

Диаметр ступицы d ₂ найдем из условия

d ₂ = (1,5 …1,6) d _к.

Его также следует согласовать с рядом значений по ГОСТ 6636.

Размер фаски f принимают в зависимости от диаметра вала [3]:

при d _к =30… 70 мм f = 2,5 мм, при d _к = 71 … 100 мм - f = 3,0 мм.

Вычислим длину сопряжения

l = l _ст –2·f

и окружную силу, действующую в зацеплении (на зубья колеса)

F_tз=2Т/d.

Вращающий момент Т определен заданием. Здесь и далее его следует подставлять в Н·мм. Значения силы получаем в ньютонах – Н.

Определяем силы, действующие на сопряжение.

Окружная сила F _t = 2 T/ D .

Осевая сила F _а = F_tз · tg β

(равна осевой силе, действующей на зубья колеса в процессе зацепления).

Радиальная сила F _r = F_tз · tg 20⁰ /cos β

(равна радиальной силе, действующей на зубья колеса в процессе зацепления).

Нормальная сила F _n = (F_tз ² + F _r²)^1/2.

Равнодействующая (суммарная) сдвигающая сила

F _R = (F _а ² + F _t²)^1/2.

Определяем минимальное давление на поверхности сопряжения из условия неподвижности соединяемых деталей под действием сдвигающей силы

.

Значения коэффициента трения f_т приведены в таблице 4 (способ сборки выберите самостоятельно).

Таблица 4. Значения коэффициента трения.

Способ сборки	Материал охватывающей детали
	сталь	чугун	Алюминиевые и магниевые стали	латунь
механический тепловой	0,06…0,13 0,14…0,16	0,07…0,12 0,07…0,09	0,02…0,06 0,05…0,06	0,05…0,10 0,05…0,14

Значение коэффициента запаса сцепления принимают в зависимости от степени ответственности узла в пределах k = 1,5 … 3,0 (выберите самостоятельно).

Минимальное значение давления из условия нераскрытия стыка

p _min2 = 6 F _a · d / (π · D · l ²) + 4 F _n /(π · D · l ).

Коэффициенты, характеризующие податливость деталей (индекс 1 для вала, 2 – для отверстия)

,

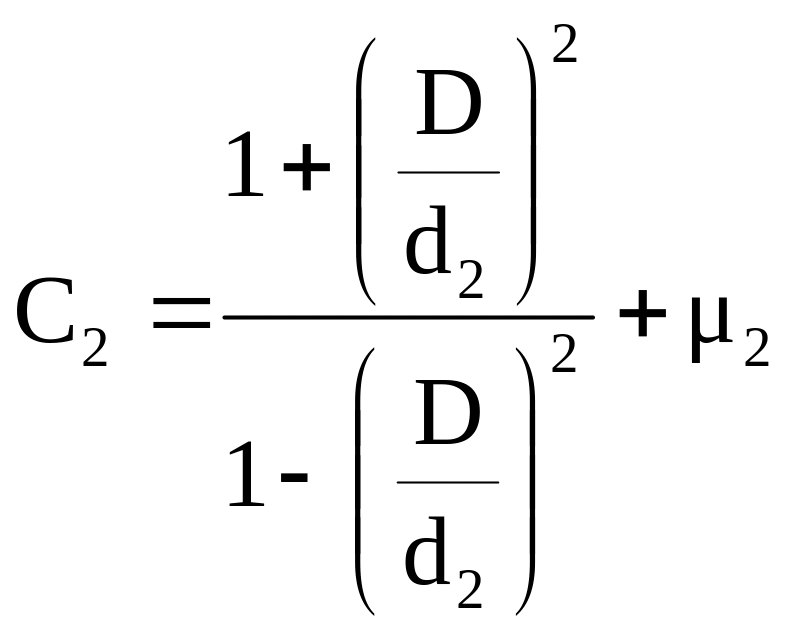где ₁ и ₂ – коэффициенты Пуассона (для стали  = 0,3); d ₀ - диаметр отверстия полого вала (в нашем случае d ₀ = 0).

Наименьший расчетный натяг

Здесь p _min - большее из полученных значений p _min1 и p _min2.

Е ₁ и Е ₂ - модули упругости (для стали Е = 2 · 10 ⁵ МПа).

Максимально допустимое давление на сопрягаемые поверхности ограничивают из условия предупреждения пластических деформаций сопрягаемых поверхностей

где _Т1 и _Т2 – предел текучести материалов вала и втулки (в соответствии с заданием _Т1 = _Т2 = _Т ).

С учетом несимметричной осевой силы и односторонней радиальной нагрузки расчетное значение максимального давления

p_{max р} = p_max – 6 F _a · d / (π · D · l ²) - 4 F _n /(π · D · l ).

где p_max - меньшее из значений p_{max 1} и p_{max 2} .

Максимальное значение натяга

Для рассматриваемой задачи существенны две поправки: на смятие неровностей и на неравномерность распределения давления по поверхности сопряжения.

Поправку на шероховатость для случая соединения стальных деталей можно вычислить по формуле

u _R = 5,5 · (Ra ₁ + Ra ₂).

Параметры шероховатости вала Ra ₁ и отверстия Ra ₂ выбирают по таблице 5 в зависимости от допусков размеров (квалитетов). Предварительно оценить номер квалитета можно из условия TD = Td = 0,5 (N _max – N _min ) по таблице 1, ориентируясь на ближайшие меньшие табличные значения допусков в интервале размеров, в который попадает значение D.

Поправку на неравномерность распределения давления по длине сопряжения u_p находим по графику (рис. 4) в зависимости от отношения длины сопряжения l к диаметру D. При l /D >1,0 принимаем u_p = 0,93.

Таблица 5. Рекомендуемые значения параметра шероховатости Ra для поверхностей деталей при посадках с натягом, мкм

Способ сборки	квалитет	поверхность	Диаметр сопряжения, мм
			До 50	Св. 50 до 120
механический	5	Вал отверстие	0,1 – 0,2 0,2 – 0,4	0,4 0,8
	6, 7	Вал отверстие	0,4 0,8	0,8 1,6
	8	Вал отверстие	0,8 1,6	0,8 – 1,6 1,6 – 3,2
термический	-	Вал отверстие	1,6 1,6-3,2

Примечание. Значения среднего арифметического отклонения профиля в указанных пределах выбирают из ряда … 0,1; 0,125; 0,16; 0,2; 0,25; 0,32; 0,4; 0,5; 0,63; 0,8; 1,0; 1,25; 1,6; 2,0; 2,5; 3,2; 4,0 … пропорционально диаметру сопряжения.

Рисунок 4 - Значения поправки u _p = p _ср / p _max. для сплошного вала (d₀=0), выступающего за края ступицы.

Вычисляем функциональные значения натягов

N _{min ф} = N _min + u _R и N _{max ф} = N _max · u _p.

По полученным значениям функциональных натягов подбираем стандартную посадку (см. пример в [1] раздел 2.2). Перечень рекомендуемых и предпочтительных (выделены жирным шрифтом) посадок для системы отверстия приведен в таблице 6.

Таблица 6. Рекомендуемые и предпочтительные посадки в системе отверстия (выборка из ГОСТ 25347).

Поле допуска отверстия	Обозначения посадок
H6	H6 H6 H6 H6 H6 H6 k5 m5 n5 p5 r5 s5
H7	H7 H7 H7 H7 H7 H7 H7 H7 H7 k6 m6 n6 p6 r6 s6 s7 t6 u7
H8	H8 H8 H8 H8 H8 H8 H8 k7 m7 n7 s7 u8 x8 z8