Механические свойства

Механические свойства определяют отношение текстильных полотен к различно приложенным внешним усилиям, вызывающим деформацию растяжения, сжатия, изгиба, а также тангенциальное сопротивление полотен и такие связанные с ним явления, как раздвижка нитей в тканях, осыпаемость, прорубаемость, спуск петель в трикотаже и др. [11]

Прочность при растяжении - важный показатель механических свойств текстильных полотен, определяющий их целостность. Сопротивление структуры полотен (систем нитей, волокон нитей и волокон) зависит от многих факторов. К ним относятся и условия деформирования (среды, скорости растяжения) и состояние структуры полотен. Известен ряд теорий прочности.

Согласно теории хрупкой прочности, впервые сформулированной А. Гриффитом, разрыв материала происходит в результате перенапряжения у вершин микротрещин (дефектов), существенно ослабляющих сопротивление элементов структуры. При достижении критического напряжения трещины растут со скоростью, близкой к скорости распространения упругих волн и затем происходит разрушение материала. А. Ф. Иоффе и его сотрудниками было экспериментально подтверждено существование микротрещин и показано, что максимальное напряжение в вершине поверхностей трещины оказывается во много раз больше напряжения, определенного отношением деформирующей нагрузки к сечению ослабленной пробы. Зависимость напряжения  от наличия дефектов или степени однородности вещества по Вейбуллу имеет вид , где А – постоянная, зависящая от природы материала и типа напряженного состояния; n – постоянная, учитывающая характер распределения дефектов или степень однородности вещества; V – рабочий объем единичной пробы.

При n в случае идеального однородного бездефектного тела прочность не зависит от объема пробы.

Согласно статистической теории хрупкой прочности А.П.Александрова и С. Н. Журкова разрыв происходит не одвременно по всей поверхности разрушения, а постепенно: начинается с самого опасного перенапряженного участка, затем распространяется в новых дефектных местах, пока в результате роста трещин не достигает критической (теоретической) величины. Однако в отличие от А. Гриффита А. П. Александров и С. Н. Журков рассматривают разрушение твердого тела как процесс, развивающийся во времени.

С. Н. Журковым и др. обоснована кинетическая (флуктуационная) теория разрушения твердых тел, согласно которой разрушение материалов происходит в результате не только механического напряжения, но и теплового движения атомов. Связи между атомами макромолекул, колеблющихся вследствие теплового движения около равновесных положений, могут разрываться тепловыми флуктуациями.

Вероятность такого разрыва зависит от начального потенциального барьера u₀, температуры Т, напряжения , снижающих начальный потенциальный барьер на величину , где  - постоянная, зависящая от структуры материала и учитывающая неоднородность распределения напряжения по микроучастку пробы и молекулярным цепям.

Тогда долговечность  материала, находящегося под, нагрузкой (напряжением ), описывается уравнением

(57)

где k—постоянная Больцмана (универсальная газовая постоянная).

Параметр ₀ не зависит от природы и структуры материала, его величина составляет 10^-1210^-13. Энергетический барьер u₀, который необходимо преодолеть при разрушении материала, соответствует энергии химических связей молекул и не зависит от межмолекулярных связей. Напряжение при разрушении зависит не только от величины потенциального барьера и₀, структурного коэффициента , но и длительности процесса растяжения .

Разрывное напряжение пробы будет тем больше, чем больше потенциальный барьер и₀ и меньше величины  и . При постоянных величинах  и и₀ на разрывное напряжение влияет лишь длительность процесса растяжения.

Однако рассмотренные теории прочности и основанные на них методы изучения прочности и долговечности текстильных полотен не получили широкого применения, хотя отдельные факторы, такие, как температура, длительность деформирования, зафиксированы в стандартах. Поэтому на практике получили использование другие характеристики механических свойств текстильных полотен при растяжении их до разрыва.

При растяжении текстильных полотен до разрыва могут быть определены следующие показатели механических свойств:

• разрывная нагрузка Р_р, Н - наибольшее усилие, выдерживаемое единичной пробой до разрыва;

• давление на пробу _п, Па, при продавливании мембраной;

• удельная разрывная нагрузка Р₀, кНм/кг, которая применяется для сравнения разрывной нагрузки текстильных полотен разной массы и рассчитывается по формуле

(58)

где Р_р – абсолютная разрывная нагрузка, Н; _S – поверхностная плотность полотна, г/м²; а_р – рабочая ширина полоски пробы, мм.

• разрывное напряжение _р, Па, - относительная нагрузка, выражающая отношение разрывной нагрузки Р_р к площади S поперечного сечения единичной пробы, на практике разрывное напряжение определяют по формуле:

(59)

При наличии элементов структуры с разной плотностью вещества нитей необходимо рассчитать средневзвешенную плотность _c кг/м³, нитей:

(60)

где _{I -}- доли нитей по массе в пробе, сопротивляющихся растяжению.

Для тканей и трикотажа разрывную нагрузку по длине (основе) и ширине (по утку) можно рассчитать с учетом массы материала разрываемой системы нитей.

(61)

или

(62)

где С – доля массы нитей той системы, по направлению которой происходит растяжение.

Удлинение при разрыве l_р, мм, представляющее собой приращение длины единичной пробы, определяют по формуле:

(63)

где L_k конечная (к моменту разрыва) длина единичной пробы, мм; L_o – длина между зажимами, мм.

Относительное удлинение при разрыве _р – это удлинение при разрыве, выраженное в процентах от первоначальной длины:

(64)

К комплексным показателям механических свойств текстильных полотен при растяжении до разрыва относится работа разрыва (абсолютная, удельная и объемная). Абсолютная работа разрыва R_р, Дж, – работа, совершаемая внешними силами при растяжении единичной пробы до разрушения. Ее рассчитывают по формуле:

(65)

где l_р – коэффициент полноты диаграммы

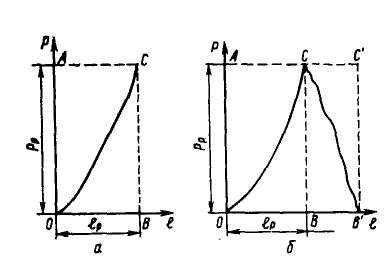
где S_ф – фактическая интегральная площадь под кривой растяжения (рис., a S_obc); S – интегральная площадь прямоугольника с координатами Р_р и l_p (S_obca) (см. рис 21).

При разрыве текстильных полотен во многих случаях разрушение пробы происходит не мгновенно, а с убыванием. Тогда полная работа

(66)

где R₂ – работа по разрушению неразорвавшихся элементарных звеньев структуры.

Рис. 21. Диаграмма растяжения элементарной пробы полотна: а – неполная; б – полная

Удельная работа разрыва rр, Дж/г, – работа разрушения структуры, от отнесенная к единице массы: (67) где МР – масса рабочей части полоски пробы, г. Объемную работу разрыва rv, Дж/см3, определяют по формуле: (68)

где V_P – объем рабочей части единичной пробы, см³.