2. Состязания в комбинационных схемах

2.1. Статические и динамические состязания сигналов

Состязания в комбинационных схемах классифицируют различным образом. В зависимости от характера переключения выходно­го сигнала схемы состязания подразделяют на статические и ди­намические.

Определение 1. Статическое состязание — это такое состя­зание сигналов, которое приводит к возможности кратковремен­ного появления на выходе комбинационной схемы сигнала 0 (или1) при переходе от одного входного состояния в другое, каждое из которых формирует на выходе неизменный сигнал 1 (или 0).

Иногда состязания в комбинационной схеме называют риском. Если при переходе между парой входных состояний, формирую­щих на выходе схемы сигнал 1, возможно кратковременное появ­ление на выходе сигнала 0, то говорят, что данный переход вызы­вает риск в единице (или статический 1-риск).

Если при переходе между парой входных состояний, форми­рующих на выходе схемы сигнал 0, возможно кратковременное появление на выходе сигнала 1, то говорят, что данный переход вызывает риск в нуле (или статический 0-риск).

Пример риска в единице приведен на рис. 7.1.

Определение 2. Динамическое состязание — это такое состя­зание сигналов, которое приводит к возможности кратковремен­ного появления на выходе комбинационной схемы сигнала 0 (или 1) при переходе от одного входного состояния в другое, первое из ко­торых формирует на выходе сигнал 1 (0), а второе — сигнал 0 (1).

Переходный процесс, соответствующий динамическому состя­занию сигналов в комбинационной схеме, приведен на рис. 7.3.

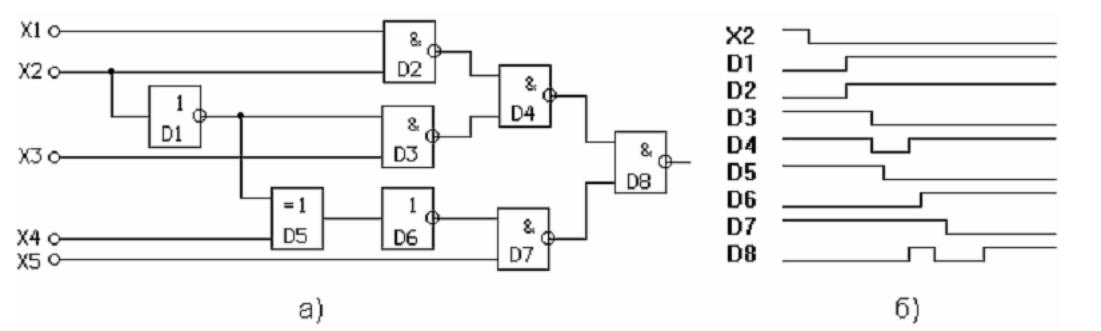
Рис. 7..3. Динамическое состязание сигналов в схеме

При переходе от входного набора X1 = X2 = ХЗ =Х4 = Х5 = 1 к набору X2 = 0, X1 = Х5 = Х4 = Х5 = 1 на выходе схемы произойдет многократное изменение сигнала, тогда как должно быть лишь од­но изменение из 0 в 1.

Динамические состязания более редки, чем статические. При динамических состязаниях первое изменение выходного сигнала всегда совпадает с требуемым переключением, поэтому их влияние на поведение схемы в целом менее опасно. В дальнейшем будем рассматривать только статические состязания.

2.2. Синтез схем, свободных от статических состязаний

Комбинационная схема считается свободной от состязаний, если ее поведение не зависит от распределения задержек в цепях прохо­ждения сигнала. Будем рассматривать только переходы между па­рами смежных входных состояний, которые формируют одно и то же значение выхода.

Два входных состояния являются смежными, если они отли­чаются значением только одной переменной.

Обычно процесс разработки комбинационных схем начинается с нахождения минимальной ДНФ (КНФ) функции. При синтезе схем без статических состязаний необходимо несколько изменить про­цедуру отыскания выражения для функции. Если используется карта Карно, то необходимо на ней выбирать покры­тия таким образом, чтобы каждая пара смежных входных наборов, на которых функция равна 1 (или 0), входила хотя бы в одно по­крытие.

Рассмотрим функцию, занесенную на карту Карно (рис. 7.4). Минимальное выражение для этой функции:

Комбинационная схема, построенная на элементах И-НЕ по этому выражению, приведена на рис. 7.1(a). В минимальном выра­жении функции два смежных входных состояния, помеченных на диаграмме буквами а и b (см. рис. 7.4), не входят в одно покрытие. Переход между этими состояниями и был рассмотрен выше (см. рис. 7.1(б)). Покрытие этой пары смежных входных состояний произведением XZ устраняет условия статического состязания.

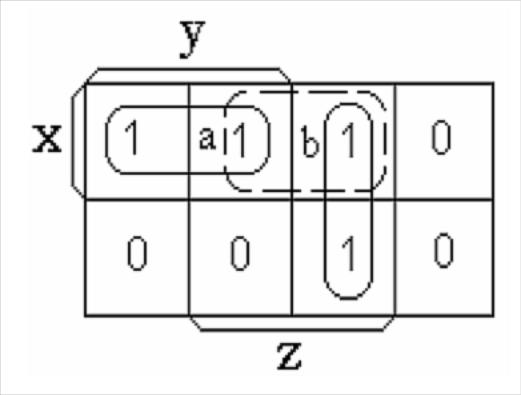
Рис. 7.4. Покрытие функции, необходимое для устранения