
- •Часть I
- •Предисловие
- •Порядок проведения лабораторных работ
- •Оформление отчета
- •1. Основные теоретические сведения
- •1.1. Законы Кирхгофа
- •1.2. Потенциальная диаграмма
- •1.3. Принцип наложения. Метод наложения
- •1.4. Теорема об эквивалентном генераторе (активном двухполюснике)
- •2. Пояснения к лабораторной установке
- •3. Порядок выполнения работы
- •3.1. Исследование источника напряжения
- •3.2. Исследование источника тока
- •3.3. Экспериментальная проверка принципа наложения и законов Кирхгофа
- •3.3.2. Измерить токи и напряжения в цепи при действии только второго источника (источник отключить переключателем п1, зашунтировав участок цепи аd). Измерить эдс источника .
- •3.4. Исследование распределения потенциала вдоль контура
- •3.5. Опытная проверка теоремы об эквивалентном генераторе
- •4. Содержание отчета
- •Контрольная карта к лабораторной работе № 1
- •1. Основные теоретические сведения
- •1.1. Синусоидальные токи и напряжения
- •1.2. Векторные диаграммы
- •1.3. Активное сопротивление, индуктивность и емкость в цепи переменного тока
- •1.4. Эквивалентные схемы приемников электроэнергии
- •1.5. Последовательное соединение катушки индуктивности и конденсатора
- •1.6. Параллельное соединение катушки индуктивности и конденсатора
- •1.7. Построение векторных диаграмм по результатам эксперимента
- •2. Пояснения к лабораторной установке
- •3. Порядок выполнения работы
- •3.1. Определение параметров эквивалентной схемы катушки индуктивности
- •3.2. Последовательное соединение катушки индуктивности и конденсатора. Резонанс напряжений
- •3.3. Параллельное соединение катушки индуктивности и конденсатора. Резонанс токов
- •4. Содержание отчета
- •Контрольная карта к лабораторной работе № 2
- •Вариант 1
- •Вариант 2
- •Вариант 3
1.2. Потенциальная диаграмма
Наглядное представление о распределении потенциала вдоль некоторого контура электрической цепи дается потенциальной диаграммой. Пример потенциальной диаграммы для контура схемы (рис. 4) приведен на рис. 5. На диаграмме по оси абсцисс откладываются значения сопротивлений участков в той последовательности,
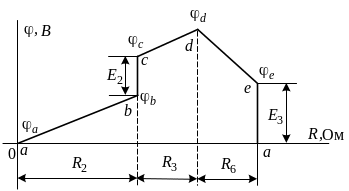
Рис. 5
в которой они
расположены в контуре, по оси ординат
– потенциалы соответствующих точек.
Потенциал произвольной точки (в данном
случае
)
принимается равным нулю. Наклон прямых
на участках диаграммы определяется
величиной тока и поэтому одинаков для
сопротивлений
![]() и
и
![]() ,
по которым протекает один и тот же ток
,
по которым протекает один и тот же ток
![]() .
При построении потенциальной диаграммы
учтено, что внутренние сопротивления
идеальных источников ЭДС равны нулю.
.
При построении потенциальной диаграммы
учтено, что внутренние сопротивления
идеальных источников ЭДС равны нулю.
1.3. Принцип наложения. Метод наложения
Для линейных электрических цепей справедлив принцип наложения, согласно которому ток в какой-либо ветви может быть представлен алгебраической суммой частичных токов, создаваемых отдельными источниками энергии. На этом принципе основывается метод расчета электрических цепей – метод наложения. Он заключается в следующем: поочередно определяют токи, возникающие от действия каждого из источников энергии, удаляя при этом остальные источники из схемы, но оставляя их внутренние сопротивления, затем находят токи в ветвях путем алгебраического сложения частичных токов. На рис. 6 рассмотрена цепь с тремя источниками ЭДС, расчет которой выполнен методом наложения.

а б в г
Рис. 6
Токи в ветвях схемы (рис. 6, а) равны алгебраической сумме частичных токов в соответствующих ветвях схем (рис. 6, б; в; г)
![]() ,
,
![]() ,
,
![]() .
.
Определение частичных токов иллюстрируется на примере расчета схемы (рис. 6, б):
 ;
;
![]() ;
;
![]() .
.
1.4. Теорема об эквивалентном генераторе (активном двухполюснике)
Двухполюсником называется электрическая схема, подключаемая к остальной схеме двумя зажимами. Если внутри двухполюсника есть источники энергии, он называется активным, если нет – пассивным.
Пассивный двухполюсник можно заменить в схеме эквивалентным сопротивлением относительно его входных зажимов (входным сопротивлением).
Теорема об эквивалентном генераторе
Активный двухполюсник может быть заменен эквивалентным генератором, ЭДС которого равна напряжению на зажимах двухполюсника при холостом ходе, а внутреннее сопротивление – входному сопротивлению соответствующего пассивного двухполюсника. Этот пассивный двухполюсник получается из активного, если исключить источники энергии, оставив в схеме их внутренние сопротивления. Ниже рассматривается применение теоремы об эквивалентном генераторе. На рис. 7, а выделенная пунктиром часть схемы является активным двухполюсником (рис. 7. б), который можно заменить эквивалентным генератором (рис. 7, в).

а б в
Рис. 7
В
этом случае по отношению к
сложная цепь в расчетном отношении
заменяется простой неразветвленной
цепью (рис. 7, в),
состоящей из ЭДС
![]() и сопротивления
и сопротивления
![]() ,
при этом
,
при этом
![]() .
.
Параметры эквивалентного генератора можно определить экспериментальным или расчетным путем. Для экспериментального определения ЭДС и внутреннего сопротивления эквивалентного генератора проводятся опыты холостого хода и короткого замыкания.
При
холостом ходе (рис. 8, а)
ветвь
![]() разомкнута,
к зажимам
подключается вольтметр (
разомкнута,
к зажимам
подключается вольтметр (![]() ),
который измеряет напряжение
),
который измеряет напряжение
![]() .
При коротком замыкании (рис. 8, б)
зажимы
замкнуты амперметром (
.
При коротком замыкании (рис. 8, б)
зажимы
замкнуты амперметром (![]() ).
Амперметр измеряет ток
).
Амперметр измеряет ток
![]() ,
откуда
,
откуда
![]() .
.
Применительно
к схеме (рис. 7, а)
расчет
и
сводится к определению
![]() на зажимах активного двухполюсника в
режиме холостого
на зажимах активного двухполюсника в
режиме холостого
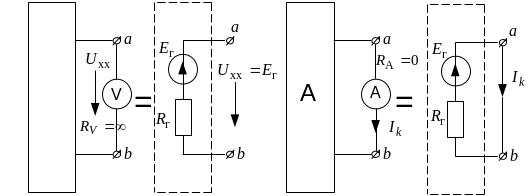
а б
Рис. 8
хода (рис. 9, а) и нахождению входного сопротивления соответствующего пассивного двухполюсника (рис. 9, б).
Для схемы (рис. 9, а)
![]() ,
,
![]() ,
,
из чего следует
![]() .
.

а б
Рис. 9
Для схемы (рис. 9, б)
![]() .
.
Теорему об эквивалентном генераторе удобно использовать при определении тока в одной из ветвей схемы при изменении сопротивления в этой ветви и при неизменных параметрах остальной части схемы, например, для схемы (рис. 7, а):
![]() ,
,
где
![]() –
измененное значение сопротивления
третьей ветви.
–
измененное значение сопротивления
третьей ветви.
