1. Основные теоретические сведения
1.1. Законы Кирхгофа
Электрическая цепь называется линейной, если она состоит из источников электроэнергии и сопротивлений, имеющих линейные вольт-амперные характеристики (ВАХ).
а
б в
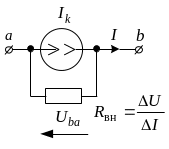
г
Рис. 1
На рис. 1 представлены: а – вольт-амперные характеристики (ВАХ) источника электрической энергии (ИЭЭ); б – схемное представление ИЭЭ; в – эквивалентная расчетная схема ИЭЭ с источником электродвижущей силы (ЭДС); г – эквивалентная расчетная схема ИЭЭ с источником тока.
Зависимость тока, протекающего по сопротивлению, от напряжения на этом сопротивлении принято называть вольт-амперной характеристикой.
Сопротивления, вольт-амперные характеристики которых являются прямыми линиями, называют линейными сопротивлениями.
На рис. 2 изображены: а – вольт-амперные характеристики линейных сопротивлений; б – схемное представление линейного сопротивления.
а б
Рис. 2
Если
ВАХ источника линейна (рис. 1, а),
то уравнение для неё записывают в виде
,
либо
,
где
–
напряжение на зажимах реального источника
при отключенной нагрузке (режим
холостого хода);
–
внутреннее сопротивление реального
источника энергии;
–
ток при коротком замыкании источника
энергии. На основании этих уравнений
реальный источник (рис. 1, б)
заменяют расчетными схемами, используя
понятие идеальных источников ЭДС (рис.
1, в)
и тока (рис. 1, г).
У
идеального
источника ЭДС
внутреннее сопротивление равно нулю!
У идеального источника тока
в
нутреннее
сопротивление равно бесконечности!
При переходе от одной расчетной схемы к другой используют соотношение
.
Если
,
то ВАХ реального источника энергии
ближе к ВАХ идеального источника ЭДС.
Если
,
то его ВАХ ближе к ВАХ идеального
источника тока.
Расчёт токов в линейной электрической цепи может быть выполнен с помощью законов Ома и Кирхгофа.
Закон Ома устанавливает прямую пропорциональность между током, протекающим по сопротивлению, и напряжением на нём:
.
Для активной ветви (рис. 3) закон Ома записывается в виде
,
где
и
– потенциалы
соответствующих
точек.
Рис. 3
Сложная электрическая цепь состоит из нескольких ветвей, объединённых в узловых точках. Каждая ветвь может содержать последовательно соединенные сопротивления и источники ЭДС.
Анализ цепи по законам Кирхгофа начинают с выбора направления токов и обхода контуров (направления и обход могут быть произвольными).
По первому закону Кирхгофа алгебраическая сумма токов в любом узле электрической цепи равна нулю:
.
По второму закону Кирхгофа в замкнутом контуре электрической цепи алгебраическая сумма падений напряжений равна алгебраической сумме ЭДС (напряжения и ЭДС, совпадающие с направлением обхода контура, берутся со знаком «+», несовпадающие – со знаком «–»).
.
Для нахождения n неизвестных токов цепи следует составить систему из n независимых уравнений. Количество независимых уравнений, составленных на основании первого закона Кирхгофа, на единицу меньше числа узлов цепи; остальные уравнения системы составляются на основании второго закона Кирхгофа для независимых контуров. Независимым называют контур, в который входит новая ветвь, не вошедшая в предыдущий контур.
Для определения трех неизвестных токов в цепи (рис. 4) достаточно составить три уравнения.
Рис. 4
По
первому закону Кирхгофа для узла
.
Для
указанных на рис. 4 направлений обхода
контуров по второму закону Кирхгофа
для контура
,
для контура
.
После определения
токов можно найти напряжения между
любыми двумя точками схемы по второму
закону Кирхгофа, например,
(рис. 4). Из уравнения, составленного
для контура
,
,
следует
.